归一化实现原理

归一化（Normalization）是一种将数据转换到相同尺度的预处理技术，它通常用于让不同特征（或数据项）具有相同的量纲或范围。在联邦学习中，归一化可以用来处理非独立同分布（Non-IID）**数据中的差异，确保不同客户端的训练过程具有可比性，从而有效地提高模型的稳定性和准确性。

1. 归一化的基本概念

归一化的目标是将数据缩放到特定的范围内，常见的范围是 [0, 1] 或 [-1, 1]。通过这种方式，可以消除数据中由于量纲差异或尺度差异带来的影响，使得不同客户端的梯度或损失值在同一个尺度上进行比较。

常用的归一化方法有：

• 最小-最大归一化（Min-Max Normalization）：将数据缩放到指定的范围（通常是 [0, 1]）。

• Z-score标准化（Z-score Normalization）：通过数据的均值和标准差对数据进行标准化。

2. 最小-最大归一化（Min-Max Normalization）

最小-最大归一化是最常用的归一化方法之一。它将数据按比例缩放到 [0, 1] 之间，公式如下：

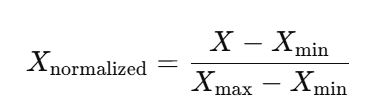
其中：

•  是原始数据（例如，客户端的损失值或梯度值）。

• 和 分别是数据中的最小值和最大值。

• 是归一化后的数据。

例子解释

假设5个客户端的损失值如下：

客户端	损失值
A	0.8
B	1.2
C	0.9
D	0.7
E	5.0

• 最小值（） = 0.7

• 最大值（） = 5.0

那么，归一化后的损失值计算如下：

• 

最终的归一化损失值如下：

客户端	原始损失值	归一化后损失值
A	0.8	0.0233
B	1.2	0.1163
C	0.9	0.0465
D	0.7	0
E	5.0	1

通过归一化方法，所有客户端的损失值都被缩放到了相同的范围内，便于进行比较。

3. Z-score标准化

Z-score标准化是另一种常见的数据归一化方法，它将数据变换为均值为0、标准差为1的分布。公式如下：

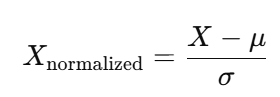
其中：

• 是原始数据（例如，客户端的损失值或梯度值）。

• 是数据的均值（所有数据的平均值）。

• 是数据的标准差（数据的离散程度）。

例子解释

假设使用上述的损失值（A: 0.8, B: 1.2, C: 0.9, D: 0.7, E: 5.0）。

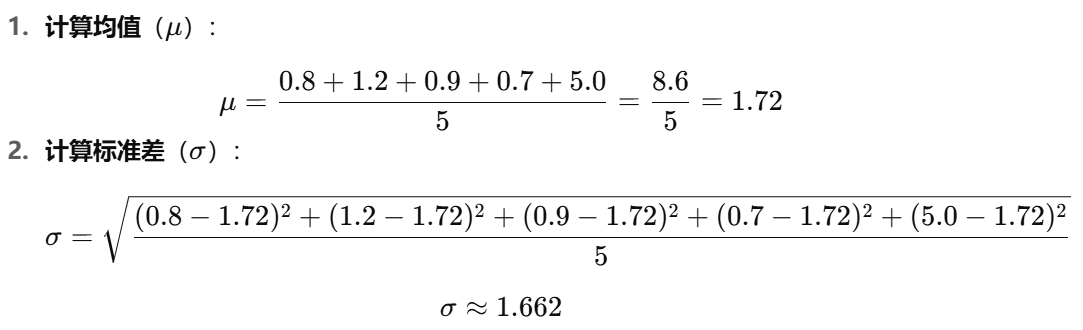
标准化后的值

最终的标准化结果：

客户端	原始损失值	标准化后损失值
A	0.8	-0.556
B	1.2	-0.313
C	0.9	-0.494
D	0.7	-0.612
E	5.0	1.993

通过Z-score标准化后，所有客户端的损失值以均值0、标准差1的方式呈现，避免了数据尺度对分析的影响。

4. 选择哪种归一化方法？

• 最小-最大归一化：适用于你已知数据的范围，并且希望将所有数据缩放到一个固定范围内。通常用于算法对特定范围敏感的情况，比如在神经网络中，激活函数（如Sigmoid）通常对归一化数据较为敏感。

• Z-score标准化：适用于数据分布较为复杂，或者你不确定数据的范围时。它不受到极端值的影响，适用于大多数基于距离的算法（如KNN、SVM等）和一些优化算法。