机器学习-第二章

2.1 监督学习概念与术语

2.1.1 欠拟合

# Python 中用于数据可视化的核心代码，它导入 matplotlib 库中专门负责绘图的 pyplot 模块，并将其简称为 plt（这是行业通用的简写，方便后续调用）
import matplotlib.pyplot as plt
#python 中用于科学计算和数值处理的核心代码，它导入了 NumPy（Numerical Python 的缩写）库，并将其简称为 np（行业通用简写，方便后续调用）。
import numpy as np
# 数据生成部分
# 生成100个在[-3, 3]区间内的随机x值
x = np.random.uniform(-3, 3, size=100)
# 将x转换为二维数组（符合sklearn模型的输入要求：[样本数, 特征数]）
X = x.reshape(-1, 1)
# 生成y值：基于二次函数y=0.5x² + x + 2，再加入正态分布噪声
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)# 数据的真实分布是二次函数关系（非线性），但加入了少量噪声（np.random.normal）使其更接近真实场景。
# 可视化的话，散点图会呈现一个抛物线的趋势。
# 从 scikit-learn 库中导入线性回归模型
from sklearn.linear_model import LinearRegression
# 实例化线性回归模型并训练
reg = LinearRegression()
# 让模型（此处为线性回归模型 reg）从输入数据中学习规律，本质是通过优化算法找到最佳参数，使模型能够拟合输入特征 X 和目标值 y 之间的关系。
reg.fit(X, y)
# 输出模型在训练集上的R²评分（越接近1越好）
print(reg.score(X, y))  # 通常会比较低（比如0.5左右）# 线性回归模型假设数据是线性关系（y = wx + b），但这里的真实关系是二次函数，因此模型无法很好地拟合数据。
# score输出的 R² 值较低，说明线性模型对数据的解释能力弱。
# 用训练好的模型预测
y_pre = reg.predict(X)
# 绘制真实数据点和预测线
plt.scatter(x, y)  # 蓝色散点：真实数据
# 红色直线：线性回归的预测结果
plt.plot(np.sort(x), y_pre[np.argsort(x)], color='r')
plt.show()
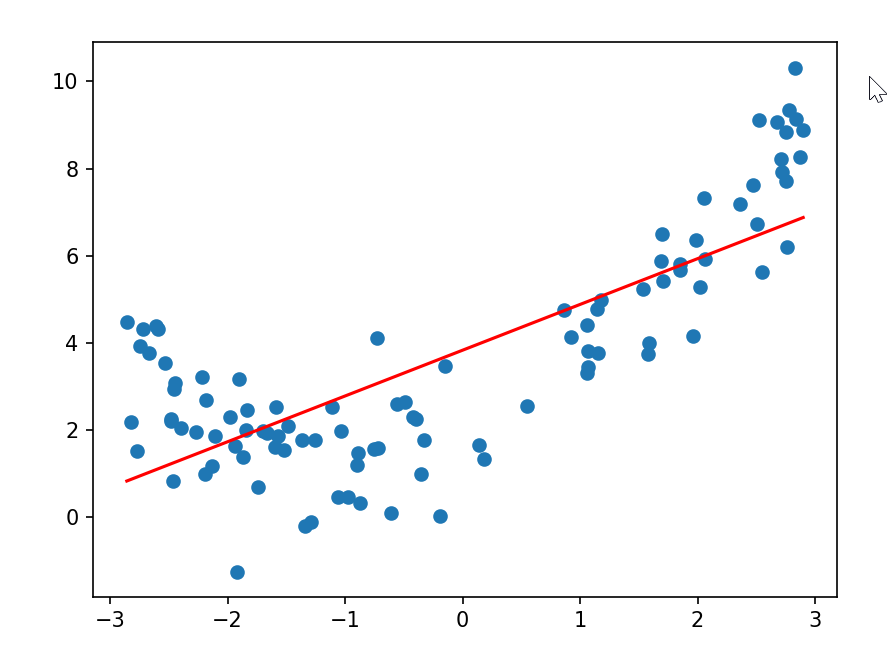
# 图像会显示：红色的直线无法贴合抛物线形状的蓝色散点，只能勉强 “穿过” 数据的中间区域，这是典型的欠拟合现象—— 模型过于简单，无法捕捉数据的非线性规律。
# from sklearn.metrics import mean_squared_error 是从 scikit-learn（Python 中常用的机器学习库）导入均方误差（Mean Squared Error, MSE） 计算函数，用于评估回归模型的预测效果。
from sklearn.metrics import mean_squared_error
mean_squared_error(y, y_pre)  # 通常会比较大（比如3-5左右）
# MSE 衡量预测值与真实值的平均平方差，值越大说明拟合效果越差。由于线性模型无法拟合二次关系，MSE 会明显偏高。

运行结果：

2.1.2 过拟合

#将Pipeline封装 方便使用
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
# 从 scikit-learn 库中导入管道（Pipeline） 类，用于将机器学习工作流中的多个处理步骤（如数据预处理、特征工程、模型训练）串联成一个整体，简化建模流程并避免数据泄露问题。
from sklearn.pipeline import Pipeline
# 从 scikit-learn 库中导入标准化处理器，用于将数据转换为均值为 0、标准差为 1的标准正态分布形式，是机器学习中最常用的数据预处理步骤之一。
from sklearn.preprocessing import StandardScaler
# 从 scikit-learn 库中导入多项式特征生成工具，用于将原始特征转换为多项式特征，从而让线性模型能够拟合非线性关系，是解决欠拟合问题的重要手段。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
# 定义了一个多项式回归的 Pipeline（管道），用于将多项式特征转换、数据标准化和线性回归三个步骤整合在一起，简化建模流程。
def PolynomialRegression(degree):return Pipeline([#构建Pipeline("poly",PolynomialFeatures(degree=degree)), # 构建PolynomialFeatures("std_scaler",StandardScaler()), # 构建归一化StandardScaler("lin_reg",LinearRegression()) # 构建线性回归LinearRegression])x=np.random.uniform(-3,3,size=100) #生成x特征 -3到3 100个
X=x.reshape(-1,1)#将x编程100行1列的矩阵
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)#模拟的是标记y 对应的是x的二次函数
'''
#设置degree=2 进行fit拟合
# poly2_reg = PolynomialRegression(2) 这行代码的作用是创建一个2 次多项式回归模型，
# 其中 PolynomialRegression 是之前定义的多项式回归管道函数，2 表示多项式的阶数（最高次项为 2 次）。
poly2_reg =PolynomialRegression(2)
poly2_reg.fit(X,y)
#采用特征的二次多项式拟合数据,求出MSE
y2_pre = poly2_reg.predict(X)
print(mean_squared_error(y2_pre,y))
plt.scatter(x,y)
plt.plot(np.sort(x),y2_pre[np.argsort(x)],color='r')
''''''
#使用degree=10，训练数据。
poly10_reg =PolynomialRegression(10)
poly10_reg.fit(X,y)
y10_pre = poly10_reg.predict(X)
print(mean_squared_error(y10_pre,y))
plt.scatter(x,y)
plt.plot(np.sort(x),y10_pre[np.argsort(x)],color='r')
'''#使用degree=100，训练数据。
poly100_reg =PolynomialRegression(100)
poly100_reg.fit(X,y)
y100_pre = poly100_reg.predict(X)
print(mean_squared_error(y100_pre,y))
plt.scatter(x,y)
plt.plot(np.sort(x),y100_pre[np.argsort(x)],color='r')plt.show()

运行结果：

（1）2次多项式拟合

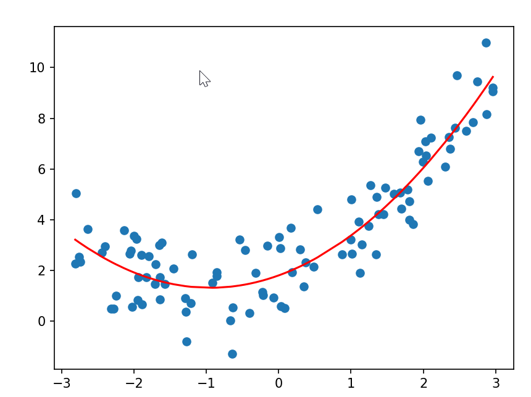
（2）10次多项式拟合

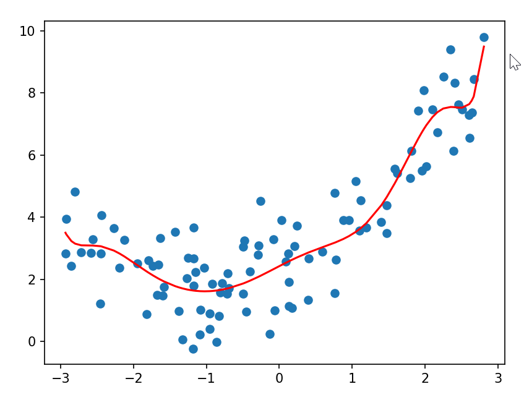
（3）100次多项式拟合

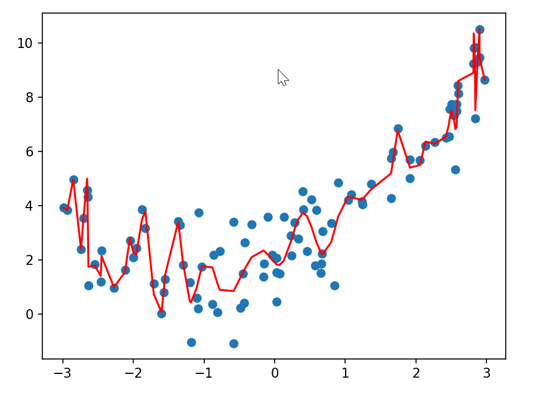
2.2 K近邻算法

2.2.1 K近邻分类

import matplotlib.pyplot as plt
import numpy as np
# 从scikit-learn库中导入生成聚类数据的工具
from sklearn.datasets import make_blobs# 手动指定3个簇的中心坐标
centers = [[-2, 2], [2, 2], [0, 4]]# 生成包含60个样本的聚类数据集
X, y = make_blobs(n_samples=60,  # 总样本数量为60个centers=centers,  # 使用定义的簇中心random_state=0,  # 随机种子，保证结果可复现cluster_std=0.60  # 每个簇的标准差，控制数据分散程度
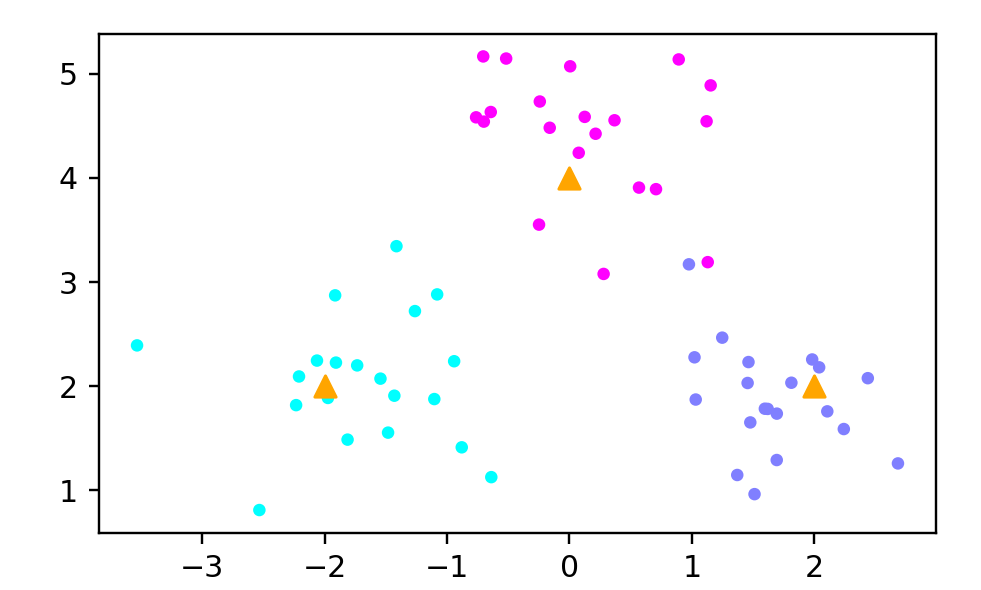
)# 创建图形并设置尺寸和分辨率
plt.figure(figsize=(5, 3), dpi=144)# 将簇中心列表转换为NumPy数组
c = np.array(centers)# 绘制样本点
plt.scatter(X[:, 0],  # 所有样本的x坐标X[:, 1],  # 所有样本的y坐标c=y,  # 根据标签分配颜色s=10,  # 样本点大小cmap='cool'  # 使用冷色调颜色映射
)# 绘制簇中心点
plt.scatter(c[:, 0],  # 所有簇中心的x坐标c[:, 1],  # 所有簇中心的y坐标s=50,  # 中心点大小（大于样本点）marker='^',  # 使用三角形标记c='orange'  # 橙色中心点
)plt.savefig('knn_centers.png')
plt.show()# 使用KNeighborsClassifier进行训练，k=5
from sklearn.neighbors import KNeighborsClassifier# 模型训练
k = 5
clf = KNeighborsClassifier(n_neighbors=k)
clf.fit(X, y)# 对新样本进行预测
X_sample = np.array([[0, 2]])
y_sample = clf.predict(X_sample)
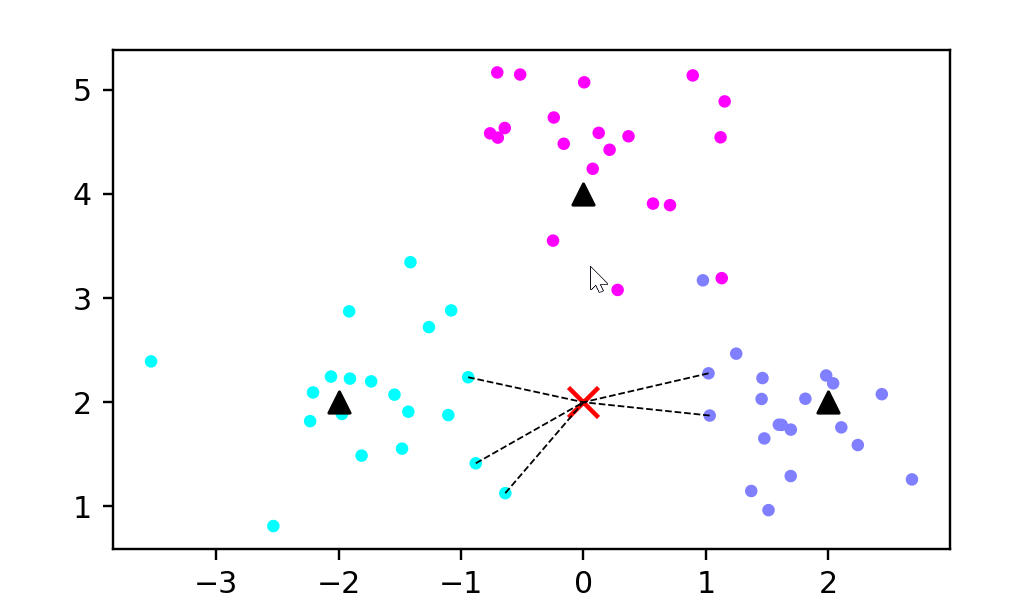
neighbors = clf.kneighbors(X_sample, return_distance=False)# 绘制预测示意图
plt.figure(figsize=(5, 3), dpi=144)
c = np.array(centers)
plt.scatter(X[:, 0], X[:, 1], c=y, s=10, cmap='cool')  # 绘制样本
plt.scatter(c[:, 0], c[:, 1], s=50, marker='^', c='k')  # 绘制中心点
plt.scatter(X_sample[0][0], X_sample[0][1], marker="x",s=100, c='red')  # 绘制待预测的点（使用红色更醒目）# 绘制预测点与最近5个样本的连线
for i in neighbors[0]:plt.plot([X[i][0], X_sample[0][0]], [X[i][1], X_sample[0][1]],'k--', linewidth=0.6)  # 虚线连接plt.savefig('knn_predict.png')
plt.show()

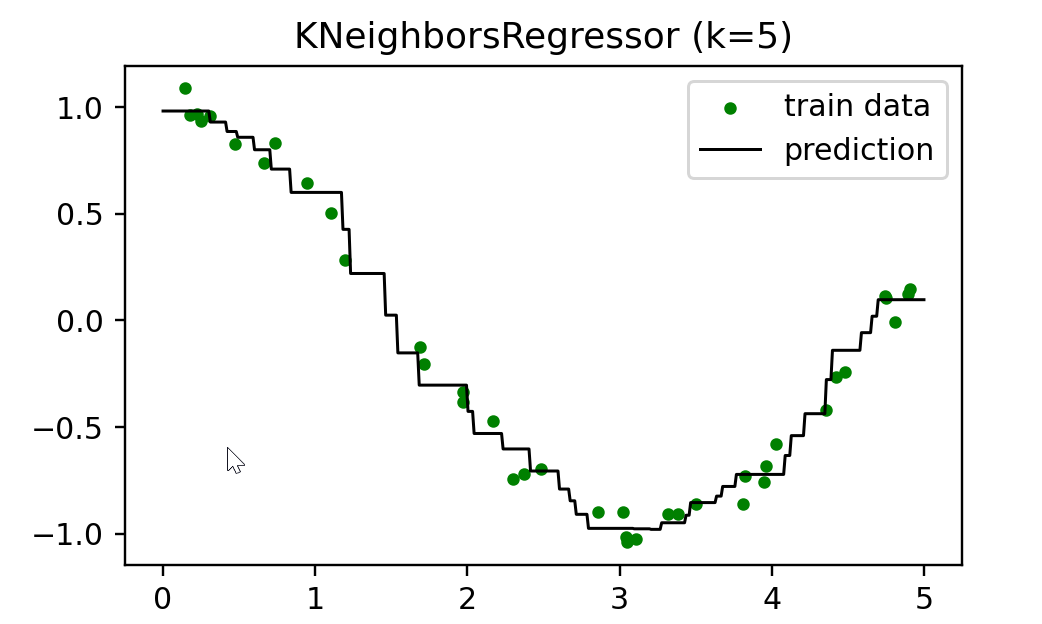
2.2.2 K近邻回归

from sklearn.neighbors import KNeighborsRegressor
import matplotlib.pyplot as plt
import numpy as np
#生成数据集，在余弦曲线的基础上加入了噪声。
n_dots = 40
X = 5 * np.random.rand(n_dots, 1)
y = np.cos(X).ravel()
# 添加一些噪声
y += 0.2 * np.random.rand(n_dots) - 0.1
#使用KNeighborsRegressor来训练模型。
# 训练模型
k = 5
knn = KNeighborsRegressor(k)
knn.fit(X, y)# 生成足够密集的点并进行预测
T = np.linspace(0, 5, 500)[:, np.newaxis]
y_pred = knn.predict(T)
print(knn.score(X, y)) # 计算拟合曲线对训练样本的拟合准确性。# 画出拟合曲线。plt.figure(figsize=(5,3), dpi=144)
plt.scatter(X, y, c='g', label='train data', s=10) #画出训练样本
plt.plot(T, y_pred, c='k', label='prediction', lw=1) # 画出拟合曲线
plt.axis('tight')
plt.title('KNeighborsRegressor (k=%i)' % k)
plt.legend()
plt.savefig('knn_regressor.png')
plt.show()