当前位置：首页 > news >正文

「日拱一码」088 机器学习——蒙特卡洛树搜索MCTS

news 2025/9/16 6:05:24

蒙特卡洛树搜索（MCTS）介绍

MCTS的四个核心步骤

MCTS的优势

代码示例：井字棋（Tic-Tac-Toe）AI

蒙特卡洛树搜索（MCTS）介绍

蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS） 是一种用于某些决策过程的启发式搜索算法，最著名的应用是在游戏人工智能领域（如AlphaGo、AlphaZero），但它也适用于其他复杂的决策问题，如机器人路径规划、自动推理和资源调度。

它的核心思想是通过随机模拟（也称为Rollout或Playout） 来智能地构建一棵不对称的搜索树，将更多的计算资源集中在更有希望的决策分支上

MCTS的四个核心步骤

MCTS通过重复执行以下四个步骤来逐步构建搜索树：

1. 选择 (Selection)

从根节点（当前状态）开始，递归地选择最优的子节点，直到到达一个未被完全展开的节点。
选择策略通常使用上限置信区间算法 (UCB1)，它在探索（尝试访问次数少的节点） 和利用（选择胜率高的节点） 之间取得平衡。
公式：

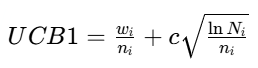
wi：该节点在模拟中获胜的次数
ni：该节点被访问的次数
Ni：父节点被访问的总次数
c：探索常数（通常为根号2），控制探索与利用的权重

2. 扩展 (Expansion)

当选择的节点不是终止状态且仍有未尝试过的动作时，为该节点创建一个（或多个）新的子节点（代表执行一个新动作后的新状态）

3. 模拟 (Simulation)

从新扩展的节点开始，运行一次随机模拟（即双方玩家都随机落子），直到游戏结束，得到一个结果（赢、输、平）

4. 回溯 (Backpropagation)

将模拟得到的结果（例如，+1 表示胜利，0 表示失败）沿着之前选择的路径（从新节点回溯到根节点）更新所有经过节点的访问次数和累计奖励（获胜次数）

MCTS的优势

不对称的树生长：算法会自发地探索更有希望的局面，忽略明显不好的选择，效率远高于暴力搜索。
无需评估函数：在游戏领域，它不需要复杂的局面评估函数，仅通过随机模拟的最终结果来评估状态的好坏。
任意时间算法：算法可以在任何时间点被中断并返回当前的最佳决策。运行时间越长，决策越精准。
适用于大型状态空间：特别适合像围棋这样分支因子巨大的游戏。

代码示例：井字棋（Tic-Tac-Toe）AI

import numpy as np
import mathclass Node:"""代表MCTS树中的一个节点。"""def __init__(self, state, parent=None, action=None):self.state = state  # 当前的游戏状态（一个3x3的numpy数组）self.parent = parentself.action = action  # 导致到达这个节点的动作（位置）self.children = []  # 子节点列表self.wins = 0  # 累计奖励（获胜次数）self.visits = 0  # 访问次数self.untried_actions = self.get_legal_actions()  # 尚未尝试过的动作def get_legal_actions(self):"""获取当前状态下所有合法的落子位置。"""return list(zip(*np.where(self.state == 0))) # 返回所有为0（空）的位置坐标def select_child(self, exploration_weight=1.4):"""使用UCB1公式从子节点中选择一个最优节点。"""# 对所有子节点计算UCB1分数，并选择分数最高的一个choices_weights = [(child.wins / child.visits) + exploration_weight * math.sqrt(math.log(self.visits) / child.visits)for child in self.children]return self.children[np.argmax(choices_weights)]def add_child(self, action, state):"""根据给定的动作，从当前节点扩展一个新的子节点。"""child = Node(state, self, action)self.untried_actions.remove(action) # 从未尝试动作列表中移除self.children.append(child)return childdef update(self, result):"""回溯更新节点的访问次数和获胜次数。"""self.visits += 1self.wins += resultdef is_terminal_node(self):"""检查当前节点是否是游戏终止节点（有人赢或平局）。"""return check_winner(self.state) is not Nonedef is_fully_expanded(self):"""检查当前节点是否已完全扩展（所有合法动作都已尝试）。"""return len(self.untried_actions) == 0def check_winner(board):"""检查棋盘状态并返回获胜者。1代表玩家1，-1代表玩家2，0代表平局，None代表游戏继续。"""# 检查行和列for i in range(3):if abs(sum(board[i, :])) == 3: return board[i, 0]  # 检查行if abs(sum(board[:, i])) == 3: return board[0, i]  # 检查列# 检查对角线if abs(board[0, 0] + board[1, 1] + board[2, 2]) == 3: return board[1, 1]if abs(board[2, 0] + board[1, 1] + board[0, 2]) == 3: return board[1, 1]# 检查平局if np.all(board != 0):return 0return Nonedef mcts(root_state, player, iteration_max=1000):"""主MCTS函数。"""root_node = Node(state=root_state)# 规定：MCTS AI总是从传入的player视角进行模拟# 在模拟中，对手是 -playerfor _ in range(iteration_max):# 1. 选择node = root_nodestate = np.copy(root_state)current_player = player# 递归选择直到一个未完全展开的节点或终止节点while node.is_fully_expanded() and not node.is_terminal_node():node = node.select_child()state[node.action] = current_playercurrent_player = -current_player # 切换玩家# 2. 扩展if not node.is_terminal_node() and not node.is_fully_expanded():action = np.random.choice(len(node.untried_actions))action = node.untried_actions[action]state[action] = current_playercurrent_player = -current_playernode = node.add_child(action, np.copy(state))# 3. 模拟sim_state = np.copy(state)sim_player = current_playerwinner = check_winner(sim_state)# 从当前状态开始随机模拟，直到游戏结束while winner is None:available_actions = list(zip(*np.where(sim_state == 0)))action = available_actions[np.random.choice(len(available_actions))]sim_state[action] = sim_playersim_player = -sim_playerwinner = check_winner(sim_state)# 4. 回溯# 从MCTS AI（root的player）的视角判断输赢# 如果模拟的获胜者是 root的player，则result=1；如果是对手，则result=0；平局为0.5if winner == 0:result = 0.5else:result = 1 if winner == player else 0# 沿着路径回溯更新所有节点while node is not None:node.update(result)node = node.parent# 对于父节点，结果需要反转，因为轮到对手下了result = 1 - result# 所有迭代完成后，选择访问次数最多的子节点作为最佳决策（更稳健的选择）best_child = max(root_node.children, key=lambda c: c.visits)return best_child.action# --- 示例用法 ---
if __name__ == "__main__":# 初始化一个空棋盘# 0: 空, 1: X, -1: Oboard = np.zeros((3, 3), dtype=int)# 假设AI是X（玩家1），人类是O（玩家-1）ai_player = 1human_player = -1# AI走第一步print("AI's turn (X):")ai_action = mcts(board, ai_player, 2000)board[ai_action] = ai_playerprint(board)# [[0 0 0]#  [0 0 1]#  [0 0 0]]