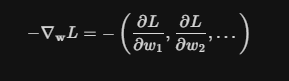简单聊聊神经网络中的反向传播
参考文章:
一文弄懂神经网络中的反向传播法——BackPropagation - Charlotte77 - 博客园
反向传播求偏导原理简单理解_反向传播偏导-CSDN博客
这篇文章是笔者在读完上述两篇参考文章后的整理或者说按照自己的理解进行的一些补充,强烈推荐先阅读上述两篇文章。这两篇文章一篇笼统的介绍了神经网络反向传播的通过链式法则计算的原理,一篇采用具体的实例进行讲解,非常易于理解。
如何优化神经网络中的权重?
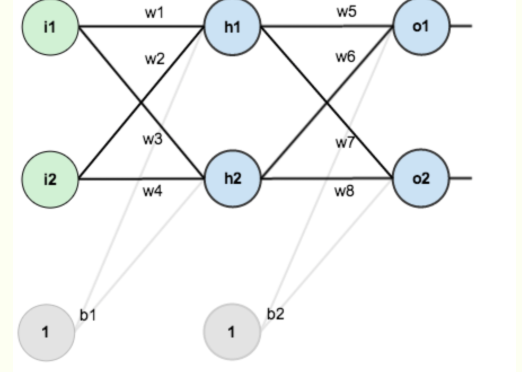
比如针对上面的这个神经网络,其中有w1,w2..b1,b2等权重参数,这些参数都是待优化的对象。一般进行优化的方式就是:计算最终的损失函数对某个权重的偏导。
比如想优化w1这个权重,那么就需要计算:这个式子的含义就是:权重w1对于最终的损失L有多少的贡献。
为什么这个式子能够表达这样的含义?需要回到偏导数的定义来看:
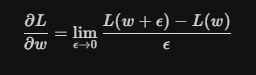
这个式子的含义就是,权重w增加一个极小的量,损失函数L变化了多少?这个变化量,其实就衡量了权重w对L的贡献。更形象的理解,假设w是一个旋钮,我极其轻微的转动了(转动量就是
)一下这个旋钮,发现最终结果变化非常大,是不是就意味着w的贡献非常大。
得到了偏导的计算结果,之后就可以通过引入一个权重因子来对参数w1进行优化:
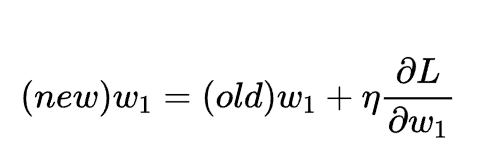
如何计算损失函数对某个权重的偏导?
针对上面的那张神经网络的情况,本质上可以用如下的计算流程进行表示。这里具体的操作如何计算损失函数对某个权重的偏导,记录在以下稿纸上。不过需要说明的几点是:
1、强烈推荐看之前的两篇参考文章,这里的计算是基于前面文章中涉及的问题的,很多地方都是自字母表示;
2、计算方向传播的过程本质上是利用链式法则,理解之后其实非常简单;
3、为了能够利用链式法则,在每一步的前向传播过程中,其实会计算临时变量比如这里的h1,o1等对各个权重的偏导,因为最终损失函数对权重的偏导需要用到这些数据;

关于梯度下降法的理解:
我们计算损失函数对某个权重的偏导,这其实只是一个维度,真正决定损失函数朝着哪个方向优化的,其实是损失函数对所有权重的偏导所构成的向量,如下公式所示: