归并排序递归与非递归实现

这篇文章笔者带领读者系统学习一下归并排序。源码仍然在github上：z-yi-han/Fundamentals-of-Data-Struct： 这是新人用来记录自己的数据结构学习的过程

归并排序的定义

首先，读者要知道什么是归并排序，其实在之前的文章中，我们写过一道链表相关的算法题，是把两个链表合成的一道题，写那道题的时候，笔者教了读者分而治之的思想，所以归并排序就是这种分而治之的思想，给定一组数据，然后将其分开，然后把分开的每一段都变成有序即可。

递归实现归并排序

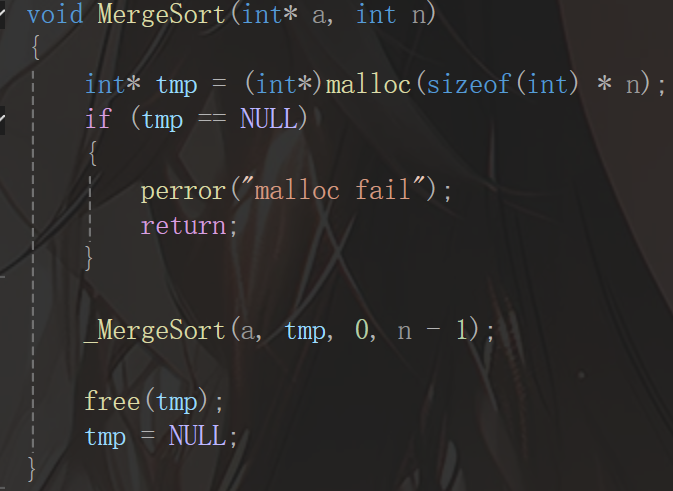
当然，主要部分在于封装的那个函数，因为tmp数组不好出现在主函数中，因此在子函数中进行功能的实现，下面给读者看一下子函数代码：

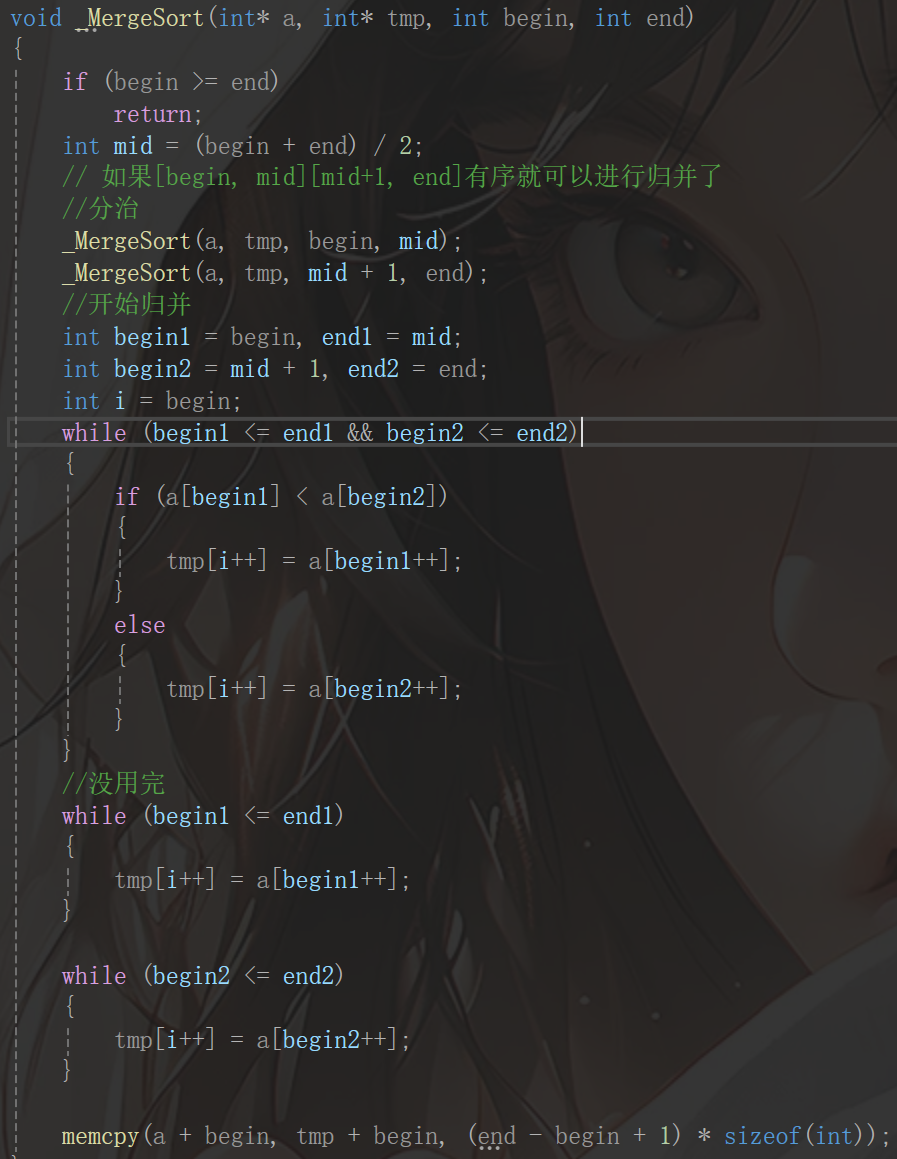
首先，我们先来过一下归并排序的思路，先正面想，给定的数据分成两份，如果这两份都是有序的，那么就分别用一个指针，比大小，然后再存储进一个第三方数组中，前后两个数组中小的先放进去，然后不断往后走，这就是单趟的逻辑。但是现在的问题是无法保证前后数组都是有序的，因此笔者用到了递归，也就是通过不断地分组，直到只有一个元素，而一个元素那必定是有序的，然后返回上一个栈帧，有两个元素，两个元素再比较即可，有序之后再往上走，就是四个元素，在往上前四个后四个全部有序，归并一下8个就会有序，依次类推即可，相信读者能感受出来，笔者刚才说的话其实就是归并排序，类似于二叉树的后序遍历，先子树再结点。然后就是最重要的归并过程了，首先分割区间直接mid即可，然后前后两段开始从头比较，小的放入tmp中，当比较完之后，剩下的部分就直接放入tmp就行。这就是用递归思想解决归并排序，在二叉树的学习之后，其实很好理解了。

非递归实现归并排序

上面的内容其实对于已经学完二叉树的读者来说相信并不难理解，接下来笔者带领读者学习用非递归法实现归并排序，这种方法对于笔者和读者来说都是不小的挑战，希望读者跟着笔者的思路认真思考。

首先，我们的目标是模拟实现递归，在之前的文章中，我们用栈来实现了递归思路进而完成了非递归实现快速排序，然而在这种情况下，真的可以用栈来模拟递归吗？这就要回到归并排序的过程了，首先归并排序是非常规则的一分为二，不断分治进而使其有序，如果我们用栈来模拟实现，没进入一次递归，出来的时候还需要一个栈来存数据，因此很麻烦，回想一下之前写的栈模拟递归实现，快排每次划分后的区间是不对称的，因为区间取决于基准，而这个基准是不确定的，因此那棵树相当不规则，而快排就是先处理一个子区间，另一个子区间留着递归，因此快排用栈更自然。总结来说：归并排序子区间规模有规律所以用循环，快排子区间规模无规律所以用栈保存剩余区间。

经过上述论述，相信读者就已经知道了，我们要用循环来模拟实现归并排序。下面我们就来改造一下原来的代码，模拟非递归实现归并排序：

首先，我们先思考循环归并的过程，其实很简答：刚开始11归并，因为最基本的有序就是一个元素，注意11归并的结果是2个元素有序，然后就22归并，以此类推即可，因此每次循环的过程都需要两个子区间，现在规定每次的长度是gap,gap分别是1，2，4，8...,其实代码已经可以出来了：

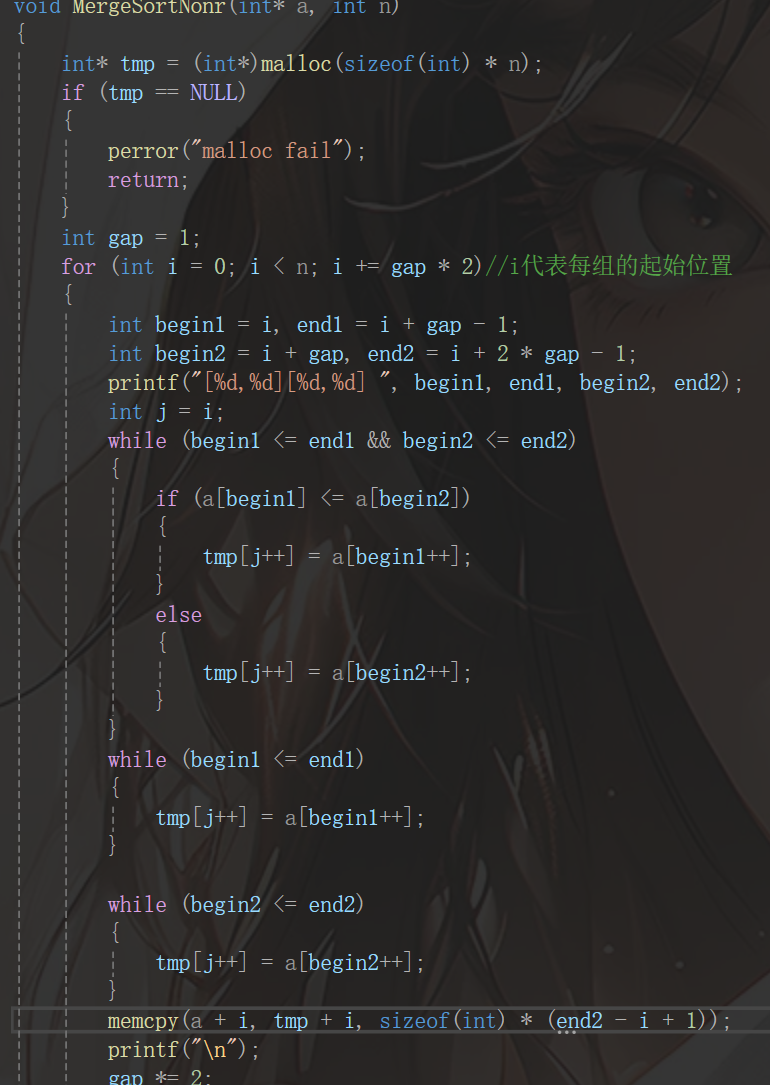
注意控制gap，gap就是每组的长度，比如11归并，gap就是1，22归并gap就是2，以gap为长度时，每次i加上gap即可 。主体代码我们已经写明白了 ，但是 有一个很严重的问题——数组会出现越界情况：这是因为我们归并的时候是按照11，22，44，88....的，因此一旦是奇数或者不是2的倍数那就会导致数组直接越界：

因此我们要想办法避免那种错误，其实这种错误一共有两类，一是右边的区间都越界，第二种是begin2未越界，end2越界了，修正的方式其实并不难，前者既然后边区间都越界 ，那么干脆不用就好了，后者只需要修正一下即可：

最后我们测试一下：

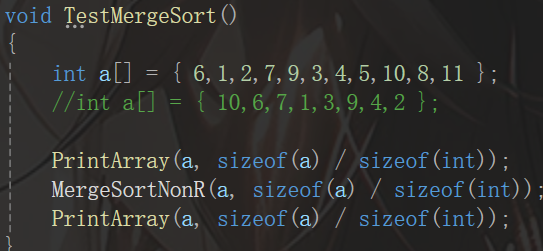
OK,本篇文章到此结束了，希望读者多支持。