当前位置：首页 > news >正文

磁共振成像原理（理论）7：射频回波 (RF Echoes)-双脉冲回波

news 2025/9/15 8:53:37

我们将讨论另一种形式的磁共振信号，称为回波 (echo)。回波信号与自由感应衰减（FID）信号的一个区别特征在于其“双侧性 (two-sidedness)”：

回波信号的一侧源于横向磁化矢量的重聚焦相位 (Rephase)，另一侧则源于去相位周期(Dephase)。所以回波信号会先变大，在减少
自由感应衰减信号只有去相位周期(Dephase)，所以信号在一开始最大，后面一直在减少。

回波信号既可以通过多个射频脉冲产生，也可以通过磁场梯度反转产生。前者产生的信号称为射频回波 (RF echoes)，后者产生的则称为梯度回波 (gradient echoes)。本节主要描述射频回波。

双脉冲回波 (Two-Pulse Echo)**

产生射频回波至少需要两个脉冲。我们从一个简单的双脉冲激发方案开始，该方案包含一个90°脉冲，随后是一个时间延迟 τ，然后再是一个180°脉冲。此激发方案表示为：
$90∘−τ−180∘(4.19)90^{\circ}-\tau-180^{\circ} \tag{4.19}$

由此产生的回波信号称为自旋回波 (Spin Echo, SE)。

为了直观地理解自旋回波是如何形成的，我们跟踪所施加脉冲的作用以及横向磁化矢量的演化过程。为简化起见，我们假设90°脉冲沿 $x^{'}$ 轴施加，180°脉冲沿 $y^{'}$ 轴施加，并且进一步假设样品在旋转坐标系中有两个进动频率分别为 $ω_s$ (慢) 和 $ω_f$ (快) 的等色团 (isochromats)。在离共振效应(或失谐)可忽略的条件下

$90x′°90_{x'}\degree$ 脉冲将两个磁化矢量都旋转到 $y^{'}$ 轴上，如下图 a 所示。
脉冲结束后，这些矢量围绕 z 轴进动。由于一个( $f$ )比另一个( $s$ )进动得相对更快（顺时针），随着自由进动的继续，它们逐渐失去相位一致性。经过时间间隔 $τ$ 后，两个矢量在横向平面上散开一个相位角 $ω_f−ω_s)τ$ ，如下图 b 所示
$180y′°180_{y'}\degree$ 脉冲将两个矢量翻转到横向平面的另一侧，如下图 c 所示
脉冲结束后，较快的矢量( $f$ )现在落后于较慢( $s$ )的矢量，其落后的相位角与180°脉冲前它领先的相位角相同。由于两个矢量将继续以角频率 $ω_f$ 和 $ω_s$ 顺时针进动（假设磁场不均匀性是时不变的），较快的等色团( $f$ )将在时间间隔 $τ\tau$ 后“追上”较慢的等色团( $s$ )，从而在时间 $t=2τt=2\tau$ 时在两个矢量之间重建相位一致性，如下图 d 所示

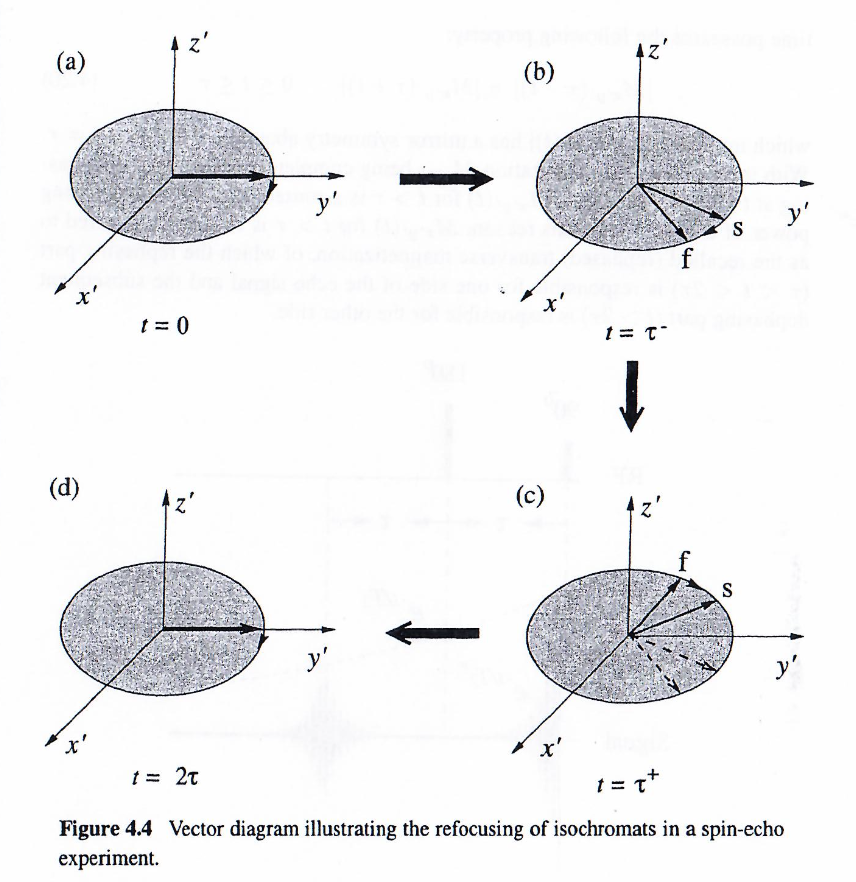
尽管上图仅展示了两组等色团的重聚相位 (rephasing) 过程，但该分析可推广至任意数量的等色团。实际上，由于真实样品中存在大量等色团，在施加 $180y′°180_{y'}\degree$ 脉冲的 $t=τt=\tau$ 时刻，去相位 (dephasing，或说失相)已经使得横向磁化矢量 $M_{x'y'}$ 完全消失，所以 FID 信号在 $t=τt=\tau$ 时消失。在 $180y′°180_{y'}\degree$ 脉冲之后， $M_{x'y'}$ 逐渐增长并在 $t=2τt=2\tau$ 时达到最大值，如下图所示。

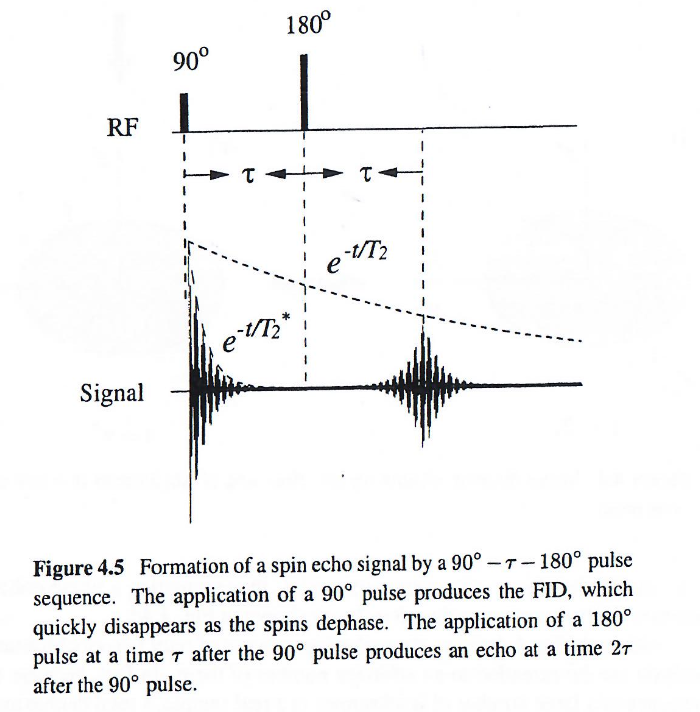
值得注意的是，上图展示了两个弛豫时间，分别是 $T_2$ 和 $T_{2}^*$ ，看得出来后者小于前者。基于之前的分析可知， $T_2$ 是因为原子核之间的相互影响（自旋-晶格、自旋-自旋相互作用）造成的，此影响是随机的，不可恢复的； $T_{2}^*$ 则是因为 $B_0$ 的不均匀造成的，此影响是工艺造成的，短时间内不随时间变化，是确定性的，可恢复的。再进一步观察，即使脉冲使得相位开始重聚，但是因为原子核之间互相影响造成的失相是不可恢复的，所以在 $t=2τt=2\tau$ 探测信号即使达到峰值，该峰值相较于 $t = 0$ 时刻，仍有 $e−2τ/T2e^{-2\tau/T_2}$ 的衰减（ $T_2$ 弛豫）。

如果我们忽略 $T_2$ 弛豫，那么在 $180y′°180_{y'}\degree$ 脉冲之前的自由进动期间导致等色团间相位一致性丢失的机制，与脉冲后导致相位一致性恢复的机制是相同的。因此， $M_{x'y'}$ 作为时间的函数具有对称特性：
$|M_{x^{\prime}y^{\prime}}(\tau-t)| = |M_{x^{\prime}y^{\prime}}(\tau+t)| \qquad 0 \leq t \leq \tau \qquad (4.20)$
该公式表明，横向磁化矢量的大小 $∣Mx′y′(t)∣|M_{x^{\prime}y^{\prime}}(t)|$ 在时间点 $\tau$ 处具有镜像对称性。即在 $\tau$ 之前某时刻 $(τ−t)(\tau - t)$ 的信号幅度，与之后相同时刻 $(τ+t)(\tau + t)$ 的信号幅度相等。由于横向磁化矢量 $M_{x'y'}$ 在 $t=τt=\tau$ 时因失相而完全消失，其在 $t>τt>\tau$ 时的“重生”是180°脉冲重聚焦能力的结果。因此， $t>τt>\tau$ 时的 $M_{x'y'}(t)$ 通常被称为被重新召集的（重聚的）横向磁化。其中，重聚部分 ( $τ<t<2τ\tau<t<2\tau$ ) 负责回波信号的一侧，而随后的失相部分 ( $t>2τt>2\tau$ ) 则负责回波信号的另一侧。

推导背景：
在 $90∘−τ−180∘90^{\circ}-\tau-180^{\circ}$ 脉冲序列中， $\tau$ 时刻（即 $180∘180^{\circ}$ 脉冲施加的时刻），由于失相，横向磁化 $Mx′y′M_{x^{\prime}y^{\prime}}$ 完全消失。 $\tau$ 时段信号的“重生”是 $180∘180^{\circ}$ 脉冲重聚焦能力的结果。因此， $\tau$ 时段的 $Mx′y′(t)M_{x^{\prime}y^{\prime}}(t)$ 常被称为 “被重新召集的（重聚焦的）横向磁化” 。其中，重聚焦部分 ( $τ<t<2τ\tau < t < 2\tau$ ) 负责回波信号的一侧，随后的失相部分 ( $2\tau$ ) 负责另一侧。

为了更一般化地推导回波信号，我们考虑以下双脉冲序列。其中 $α1\alpha_1$ 和 $α2\alpha_2$ 是两个任意角度的射频脉冲， $τ\tau$ 是时间间隔。
$\alpha_{1} - \tau - \alpha_{2} \tag {4.21}$

假设这两个脉冲都是 $y^{'}$ 方向的，在开始正式的分析前，我们先来回顾 $αy′\alpha_{y^{\prime}}$ 脉冲和时间 $τ\tau$ 对宏观磁化分量的影响，首先是脉冲 $αy′\alpha_{y^{\prime}}$ 前后的转换：
$\begin{bmatrix} M_{x^{\prime}} \\ M_{y^{\prime}} \\ M_{z^{\prime}} \end{bmatrix} \stackrel{{\alpha_{y^{\prime}}}}{\longrightarrow} \begin{bmatrix} M_{x^{\prime}}\cos\alpha - M_{z^{\prime}}\sin\alpha \\ M_{y^{\prime}} \\ M_{x^{\prime}}\sin\alpha + M_{z^{\prime}}\cos\alpha \end{bmatrix} \tag {4.22}$

此矩阵变换描述了在旋转坐标系中，一个沿 $y^{'}$ 轴施加、翻转角为 $α\alpha$ 的射频脉冲对磁化矢量各分量 $(Mx′,My′,Mz′)(M_{x^{\prime}}, M_{y^{\prime}}, M_{z^{\prime}})$ 的影响。该脉冲会混合 $x^{'}$ 和 $z^{'}$ 分量，而 $y^{'}$ 分量保持不变。

下面的公式描述了磁化矢量在时间间隔 $τ\tau$ 内的演化
$\begin{bmatrix} M_{x^{\prime}} \\ M_{y^{\prime}} \\ M_{z^{\prime}} \end{bmatrix} \stackrel{{\tau}}{\longrightarrow} \begin{bmatrix} (M_{x^{\prime}}\cos\omega\tau + M_{y^{\prime}}\sin\omega\tau)e^{-\tau/T_{2}} \\ (-M_{x^{\prime}}\sin\omega\tau + M_{y^{\prime}}\cos\omega\tau)e^{-\tau/T_{2}} \\ M_{z}^{0}(1 - e^{-\tau/T_{1}}) + M_{z^{\prime}}e^{-\tau/T_{1}} \end{bmatrix} \tag {4.23}$

横向分量 ( $Mx′,My′M_{x^{\prime}}, M_{y^{\prime}}$ )：以频率 $ω\omega$ 在横向平面内进动（ $cos⁡ωτ\cos\omega\tau$ 和 $sin⁡ωτ\sin\omega\tau$ 项），同时其幅度以时间常数 $T_2$ 指数衰减 ( $e−τ/T2e^{-\tau/T_{2}}$ )。
纵向分量 ( $Mz′M_{z^{\prime}}$ )：以时间常数 $T_1$ 弛豫恢复至其热平衡值 $M_{z}^{0}$ 。

正式开始分析双脉冲序列，考虑一个频率为 $ω\omega$ 的任意等色团，初始处于热平衡状态（只有 $Mz0(ω)M_{z}^{0}(\omega)$ ）。在施加 $α1,y′\alpha_{1,y'}$ 脉冲后瞬间，其磁化分量为：
$\begin{align*} M_{x^{\prime}}(\omega, 0_{+}) &= -M_{z}^{0}(\omega)\sin\alpha_{1} \\ M_{y^{\prime}}(\omega, 0_{+}) &= 0 \\ M_{z^{\prime}}(\omega, 0_{+}) &= M_{z}^{0}(\omega)\cos\alpha_{1} \end{align*}$

经过 $τ\tau$ 延迟后，磁化分量演化为：
$\begin{align*} M_{x^{\prime}}(\omega, \tau) &= -M_{z}^{0}(\omega)\sin\alpha_{1} \cos\omega\tau e^{-\tau/T_{2}} \tag {4.24a} \\ M_{y^{\prime}}(\omega, \tau) &= M_{z}^{0}(\omega)\sin\alpha_{1} \sin\omega\tau e^{-\tau/T_{2}} \tag {4.24b} \\ M_{z^{\prime}}(\omega, \tau) &= M_{z}^{0}(\omega)[1 - e^{-\tau/T_{1}}] + M_{z}^{0}(\omega)\cos\alpha_{1} e^{-\tau/T_{1}} \\ &= M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau/T_{1}}] \tag {4.24c} \end{align*}$

推导解释：

将初始热平衡值 $0, 0, M_z^0)$ 代入脉冲变换公式 (4.22)，得到 $0_+$ 时刻的值。
再将 $0_+$ 时刻的值代入自由演化公式 (4.23)，并经过代数整理，得到 $τ\tau$ 时刻的各分量表达式。
(4.24c) 中的简化展示了纵向弛豫的最终表达式，它由两部分组成：从零恢复的部分 ( $1−e−τ/T11-e^{-\tau/T_1}$ ) 和从初始值 $Mz0cos⁡α1M_z^0 \cos\alpha_1$ 衰减的部分( $e−τ/T1e^{-\tau/T_1}$ ) 。

$α2\alpha_2$ 脉冲对 $y^{'}$ 分量没有影响，但将 $τ\tau$ 时刻的 $x^{'}$ 和 $z^{'}$ 分量变换为以下新值：
$\begin{align*} M_{x^{\prime}}(\omega, \tau_{+}) &= -M_{z}^{0}(\omega)\sin\alpha_{1}\cos\alpha_{2} \cos\omega\tau e^{-\tau/T_{2}} \\ &\quad - M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau/T_{1}}] \sin\alpha_{2} \tag {4.25a} \\ M_{z^{\prime}}(\omega, \tau_{+}) &= M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau/T_{1}}] \cos\alpha_{2} \\ &\quad - M_{z}^{0}(\omega)\sin\alpha_{1} \sin\alpha_{2} \cos\omega\tau e^{-\tau/T_{2}} \tag {4.25b} \end{align*}$
将 $τ\tau$ 时刻的磁化矢量 $[Mx′(τ),My′(τ),Mz′(τ)][M_{x^{\prime}}(\tau), M_{y^{\prime}}(\tau), M_{z^{\prime}}(\tau)]$ 作为公式 (4.22) 的输入，施加 $αy′\alpha_{y'}$ 脉冲（此处 $α=α2\alpha = \alpha_2$ ），即可得到这些表达式。 $My′M_{y^{\prime}}$ 分量的变换未列出，因为 $αy′\alpha_{y'}$ 脉冲对齐没有影响

通过三角恒等式 $cos⁡α2=cos⁡2α22−sin⁡2α22\cos\alpha_2 = \cos^2\frac{\alpha_2}{2} - \sin^2\frac{\alpha_2}{2}$ ，对 (4.25a) 的第一项进行了代数变形， $τ+\tau_+$ 时刻的 $x^{'}$ 分量可以重写为：
$\begin{align*} M_{x^{\prime}}(\omega, \tau_{+}) &= -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} \cos\omega\tau e^{-\tau/T_{2}} \\ &\quad + M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} \cos\omega\tau e^{-\tau/T_{2}} \\ &\quad - M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau/T_{1}}] \sin\alpha_{2} \tag {4.26} \end{align*}$
利用 $\cos^2\frac{\alpha_2}{2} + \sin^2\frac{\alpha_2}{2}$ 对 (4.24b) 的第一项进行了代数变形， $τ+\tau_+$ 时刻的 $y^{'}$ 分量可以重写为：
$\begin{align*} M_{y^{\prime}}(\omega,\tau_{+})&=M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}\sin\omega\tau e^{-\tau/T_{2}}\\ &\quad+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\sin\omega\tau e^{-\tau/T_{2}} \end{align*}\tag {4.27}$

将 $τ+\tau_+$ 时刻的 $x^{'}$ 和 $y^{'}$ 磁化分量组合成了复横向磁化矢量 $M_{x'y'} = M_{x'} + iM_{y'}$ 的紧凑形式（此处的 $ωτ\omega\tau$ 是顺时针和 $x^{'}$ 的角度，而欧拉公式的角度是逆时针和 $x^{'}$ 的角度）：
$\begin{align*} M_{x^{\prime}y^{\prime}}(\omega,\tau_{+})\,=\,&\,M_{z}^{0}(\omega)\sin\alpha_{1}\left(\sin^{2}\frac{\alpha_{2}}{2}e^{-i\omega\tau}-\cos^{2}\frac{\alpha_{2}}{2}e^{i\omega\tau}\right)e^{-\tau/T_{2}}\\ &\,-M_{z}^{0}(\omega)[1-(1-\cos\alpha_{1})e^{-\tau/T_{1}}]\sin\alpha_{2} \end{align*}\tag {4.28}$

第一项 (横向部分): $Mz0(ω)sin⁡α1(sin⁡2α22e−iωτ−cos⁡2α22eiωτ)e−τ/T2M_{z}^{0}(\omega)\sin\alpha_{1}\left(\sin^{2}\frac{\alpha_{2}}{2}e^{-i\omega\tau}-\cos^{2}\frac{\alpha_{2}}{2}e^{i\omega\tau}\right)e^{-\tau/T_{2}}$

该项包含了由前两个脉冲产生的横向磁化，其演化与频率 $ω\omega$ 和 $T_2$ 弛豫相关。
第二项 (纵向衍生部分): $−Mz0(ω)[1−(1−cos⁡α1)e−τ/T1]sin⁡α2-M_{z}^{0}(\omega)[1-(1-\cos\alpha_{1})e^{-\tau/T_{1}}]\sin\alpha_{2}$
该项源于第二个脉冲 ( $α2\alpha_2$ ) 作用于 $τ\tau$ 时刻的纵向磁化 $Mz′(ω,τ)M_{z'}(\omega, \tau)$ 。这部分磁化在脉冲前是纵向的，脉冲后其一部分被扳倒到横向平面，但其相位与频率 $ω\omega$ 无关。

下面的公式描述了第二个脉冲之后 ( $\tau$ )，复横向磁化矢量在旋转坐标系中的自由进动和弛豫演化。
$\begin{align*} M_{x^{\prime}y^{\prime}}(\omega,t)&=M_{x^{\prime}y^{\prime}}(\omega,\tau_{+})e^{-(t-\tau)/T_{2}}e^{-i\omega(t-\tau)}\\ &=M_{z}^{0}(\omega)\sin\alpha_{1}\left(-\cos^{2}\frac{\alpha_{2}}{2}e^{-i\omega\tau}+\sin^{2}\frac{\alpha_{2}}{2}e^{i\omega\tau}\right)e^{-t/T_{2}}e^{-i\omega(t-\tau)}\\ &\quad-M_{z}^{0}(\omega)[1-(1-\cos\alpha_{1})e^{-\tau/T_{1}}]\sin\alpha_{2}e^{-(t-\tau)/T_{2}}e^{-i\omega(t- \tau)}\\ &=M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-t/T_{2}}e^{-i\omega(t-2\tau)}\\ &\quad-M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-t/T_{2}}e^{-i\omega t}\\ &\quad-M_{z}^{0}(\omega)[1-(1-\cos\alpha_{1})e^{-\tau/T_{1}}]\sin\alpha_{2}e^{-(t-\tau)/T_{2}}e^{-i\omega(t-\tau)} \end{align*}\tag{4.29}$
第一行 (通用演化公式):
$Mx′y′(ω,t)=Mx′y′(ω,τ+)e−(t−τ)/T2e−iω(t−τ)M_{x^{\prime}y^{\prime}}(\omega,t) = M_{x^{\prime}y^{\prime}}(\omega,\tau_{+}) e^{-(t-\tau)/T_{2}} e^{-i\omega(t-\tau)}$
- 这是旋转坐标系中磁化矢量演化的标准形式：幅度以 $T_2$ 时间常数指数衰减 ( $e−(t−τ)/T2e^{-(t-\tau)/T_{2}}$ )，同时以频率 $ω\omega$ 绕 $z^{'}$ 轴进动 ( $e−iω(t−τ)e^{-i\omega(t-\tau)}$ )。
后续行 (展开式):
将公式 (4.28) 代入第一行的通用公式，并进行代数展开和整理，得到三项。

仔细的查看这三项，他们都适用于 ( $\tau$ )：
第一项： $Mz0(ω)sin⁡α1sin⁡2α22e−t/T2e−iω(t−2τ)M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-t/T_{2}}e^{-i\omega(t-2\tau)}$ ：包含相位因子 $e−iω(t−2τ)e^{-i\omega(t-2\tau)}$ 。当 $2\tau$ 时，此因子变为 $e^{0} = 1$ ，意味着所有频率成分的相位在该时刻都会重新回到0相位，这标志着回波的形成，这个过程就是相位重聚。

第二项： $−Mz0(ω)sin⁡α1cos⁡2α22e−t/T2e−iωt-M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-t/T_{2}}e^{-i\omega t}$ ：包含相位因子 $−iωt^{-i\omega t}$ ，不同频率成分会有不同的相位。当这些不同频率横向宏观磁化矢量成分叠加后，因为相位的不一致而快速减弱。

第三项： $−Mz0(ω)[1−(1−cos⁡α1)e−τ/T1]sin⁡α2e−(t−τ)/T2e−iω(t−τ)-M_{z}^{0}(\omega)[1-(1-\cos\alpha_{1})e^{-\tau/T_{1}}]\sin\alpha_{2}e^{-(t-\tau)/T_{2}}e^{-i\omega(t-\tau)}$ ：包含相位因子 $e−iω(t−τ)e^{-i\omega(t-\tau)}$ ，不同频率成分会有不同的相位。当这些不同频率横向宏观磁化矢量成分叠加后，因为相位的不一致而快速减弱。

对一个存在频谱分布的系统而言，第二项和第三项都是一个纯失相项，而第一项在逐渐的聚相。在当 $2\tau$ 时，该项产生了一个回波信号，它可以被表达为：
$S(t)=\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\int_{-\infty}^{\infty}\rho(\omega)e^{-t/T_{2}(\omega)}e^{-i\omega(t-T_{E})}d\omega, when |t-T_{E}|\leq T_{acq}/2\tag {4.30}$
其中：

$TE=2τT_{E}=2\tau$ ，是回波的峰值发生的时刻
$T_{acq}$ ，是数据采样间隔，表示信号在回波峰附近的一个时间窗口（数据采集间隔）内被记录
$ρ(ω)\rho(\omega)$ : 质子密度谱，表示不同进动频率的质子分布。
$e−t/T2(ω)e^{-t/T_{2}(\omega)}$ : $T_2$ 弛豫衰减因子，导致信号随时间指数衰减。
$e−iω(t−TE)e^{-i\omega(t-T_{E})}$ : 相位演化因子。当 $T_E = 2\tau$ 时，此项为 1，所有频率成分同相位，信号达到最大值（回波峰）。

回波时间 $t=T_E$ 时刻测得的回波峰值振幅 $A_E$ 为
$A_{E}=\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\int_{-\infty}^{\infty}\rho(\omega)e^{-T_{E}/T_{2}(\omega)}d\omega\tag {4.31}$

假设 $T_2$ 与空间位置（进而与频率 $ω\omega$ ）无关，上式可以进一步简化为
$A_{E}=M_{z}^{0}\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-T_{E}/T_{2}}\tag {4.32}$
当 $α1=90∘\alpha_1 = 90^{\circ}$ 和 $α2=180∘\alpha_2 = 180^{\circ}$ 时， $sin⁡α1sin⁡2α22=1∗1=1\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} = 1 * 1 = 1$ ，得到最大可能的回波振幅 $A_{E}^{max} = M_{z}^{0} e^{-T_{E}/T_{2}}$ 。这仍比初始 FID 的最大值 () 小倍，原因是 $T_2$ 弛豫（随机波动）不可逆，无法被重聚焦脉冲恢复。