手搓多模态-10 旋转位置编码的原理和实现

前情回顾

这几个月以来，一直忙于工作，暂时没有时间维护博客和文章。最近得以忙里偷闲，思前想后决定还是花时间把之前没能写完的博客好好地再完善一下。博主最近在看一些强化学习的工作，后面也会在博客中更新强化学习的原理。

在手搓多模态这个专栏，我们之前已经完成了主模型的构建工作，但是我们尚未提供旋转位置编码的实现细节，于是本文继续延续之前的内容，并完成旋转位置编码的原理和实现。

旋转位置编码的介绍

旋转位置编码是相对位置编码中的一员，它主要通过旋转的方式来为不同位置的Token嵌入打上位置的标记。在直接介绍旋转位置编码之前，我们首先引入经典位置编码的分析，从而避免因直接讲解旋转位置编码而带来突兀。

经典位置编码

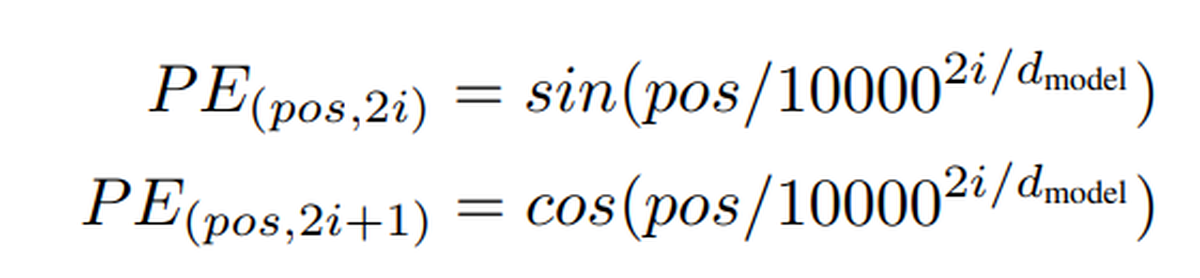
上面是经典位置编码的数学计算公式，其中 pos 表示Token在序列中的绝对位置，2i或者2i+1都表示在针对某个Token的嵌入向量的第2i(2i+1)维，表示Token编码的嵌入维度。

有的人可能会诧异：为什么位置编码长这样呢？或者说为什么这样的位置编码行之有效呢？

要理解这一点，我们需要了解位置编码在解决什么问题。

在Transformer中，序列输入首先会被Embedding层转化为Token Embedding，每个Token一般会被转换为一个固定维度(如4096维)的向量，这一过程是并行发生的。然后Token Embedding会经历编码器和解码器，最后生成一个预测的Embedding logits（概率分布）。

但这些过程目前都是并行发生的，这意味着，即使输入序列的Token随意变换顺序，它们参与的计算，生成的概率分布也不会发生改变，但显然这与我们的直觉完全不符合（比如“你与我打招呼”和“我与你打招呼”所表达的语义信息是不同的）。因为Token之间目前并没有显式地编码任何与位置相关的信息进去。

那为了要让Token之间的计算具备一些位置信息，就需要在第一次注意力计算之前就把位置Embedding到Token的嵌入向量中。一个比较直观能想到的方案是在Token的嵌入上做文章，构建一个与Token向量同维度的且包含位置信息的向量，并叠加上去（有的人可能会说，那为什么不在Token没被编码的时候做文章呢？为什么是叠加不是相乘呢？ 因为这里只是一种方案而已，你可以尝试采用别的方案，只是原作者是采取了这种简单直观的方案而已）。

假定某个位置为pos的Embedding为  , 位置编码向量为

其中f是位置编码函数，故编码了位置信息的Embedding为

后续Embedding会参与注意力计算，主要是QKV的矩阵乘积，那么必然会引入, 而这里因为位置编码是向量，所以这里实际上是在做向量内积。那么假定位置编码函数可以写成以下形式：

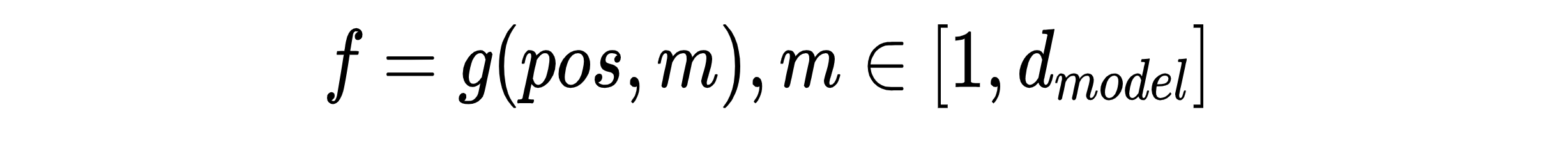假定嵌入的维度为2，那么我们对不同Token取内积来看看，设对前pos_1与pos_2的Embedding求内积的结果为w：

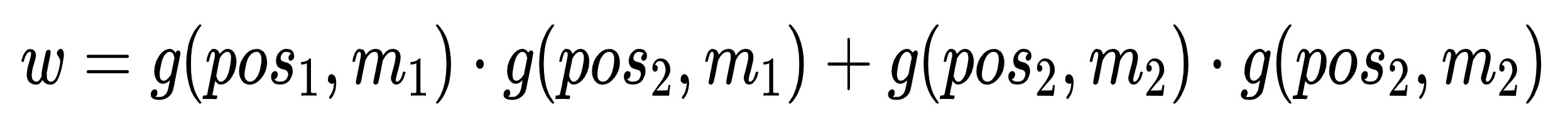
这里其实已经可以看出一些眉目了，因为我们其实希望这里可以反应出两个Token的相对位置关系，这种位置关系假定可以用h来建模，则w应当可以写成如下形式：

则有：

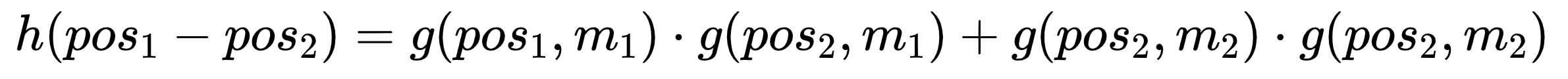
这种形式的公式很容易让人想到三角函数中的和差化积公式：

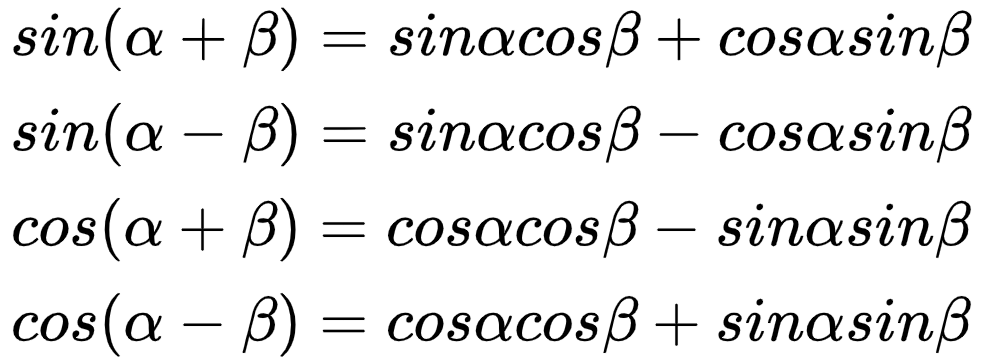
也因此研究人员想到把位置编码用三角函数编码，那此时只需要让位置编码向量中的不同维度的信息置为关于pos与m三角函数即可。最简单的想法是直接让三角函数的角度为pos与m的乘积，就如下所示：

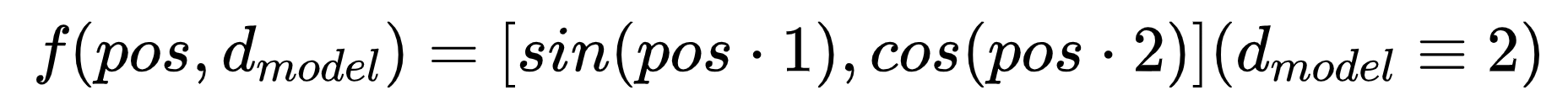
但这样是没法建模成我们刚刚的形式的，带入内积的计算即可知道：

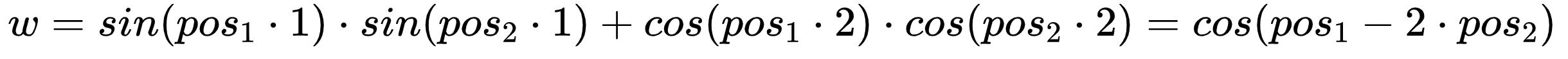
这样得到的映射并非是 的建模，而是 的建模，归根结底是因为和差化积公式中要想建模 则在位置编码时，它们的系数不同导致的，所以我们必须把系数抹除掉，那就得到了以下这样的位置编码函数：

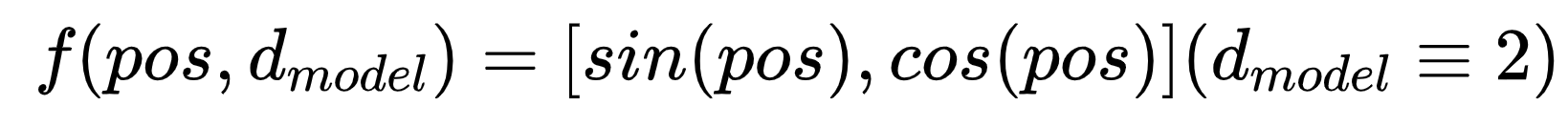
但前面我们算内积，只考虑了嵌入向量维度为2的情况。实际的嵌入向量会有512甚至更高维度。有人可能说，那直接扩展到高维，然后重复交替这两个值就行了，如下：

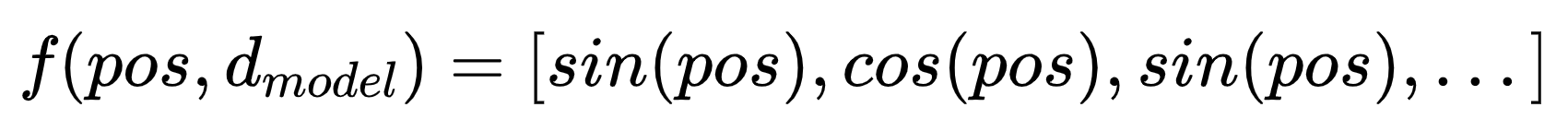
这样显而易见是很容易扩展到高维度的，但是伴随着出现了一个问题，就是三角函数的周期性。不妨试想，在维度为2的时候，模型通过QKV的乘积中的一些变换得到了以下结果：

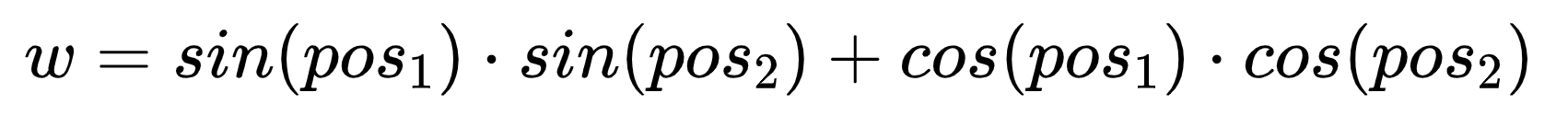
这里实则得到的是,这里的T为三角函数的周期，那么这样子的话其实没办法解出两个token的相对位置信息，因为它们直接增加若干个三角函数周期都是可以满足这个等式的（这里需要考虑计算机处理浮点数的精度问题）。所以理论上这样没法精确地把相对位置信息传递给模型。

于是研究人员想到在扩展到高维时，给pos前面加上一个与维度相关的系数，假定为a, 那就可以写成如下的形式：

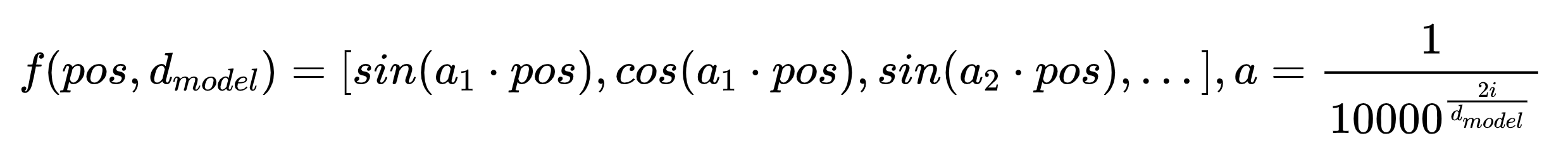
这样的话，最后模型能够通过每组三角函数（即位置编码向量中相邻的sin函数和cos函数）解读出的信息是这样：

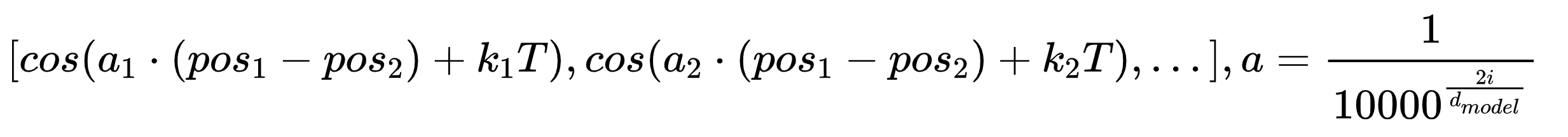
那这里可以列出这样的线性方程组(在位置编码的维度数足够高的情况下)：

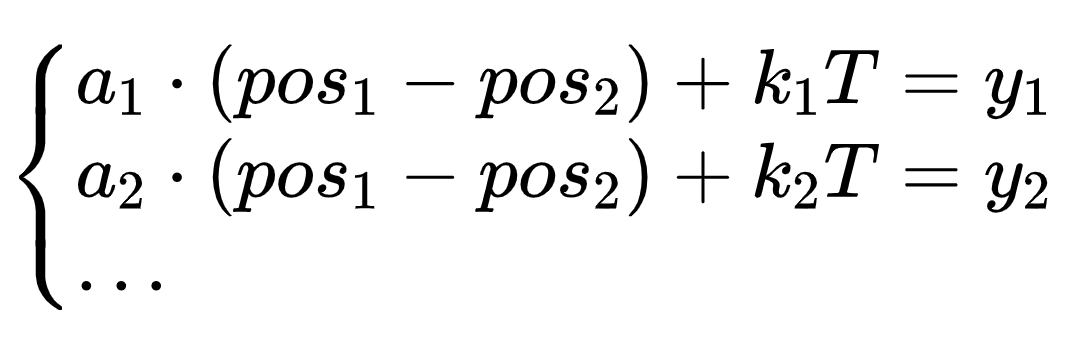
这里面只有 和k1,k2...不知道，其他信息都是知道的，a是系数（设计的原则是a在不同维度的值是不一样的），T是三角函数周期，y是由三角函数的值反推出的角度，理论上只要维度数足够，则能辅助模型求出 ，这里虽然是非满秩的，但是因为潜在的k是整数的条件则可以帮助模型判断。当然严格的数学证明博主就没办法给出了，这里已经足够我们来理解位置编码了，那么我们再来看看这个系数a，它是这么定义的：

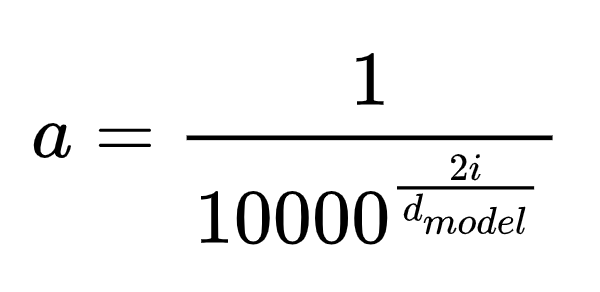
这里可以看到它的分母随着维度的增高在增大，则系数a在减小，这样导致了位置编码中高维三角函数的系数小，周期大，频率小；低维度三角函数的系数大，周期小，频率大，从位置编码的图像上我们也可以看到这一点：

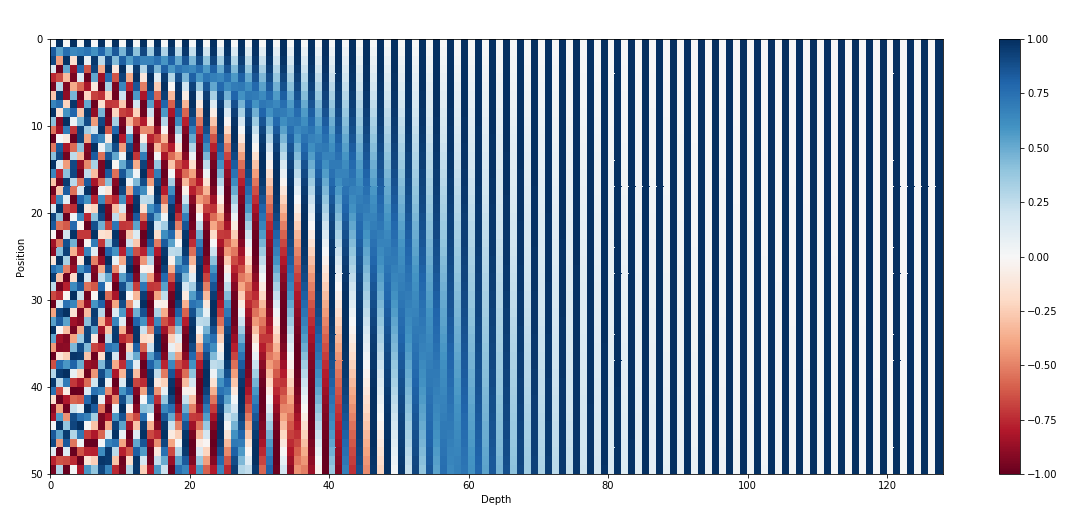
高维列(右边的列)的变换频率低，低维列(左边的列)的变换频率高。而之所以将a的分母的底数设置为10000，是为了防止不同的pos的位置编码恰好相同，假如pos_2正好导致Token_2的所有维度位置编码的三角函数与Token_1的位置编码差了整数个周期，则它们的位置编码就可能完全一样，所以为了防止这一点，就应当使得最高维的周期足够大，这样必须非常非常大才有可能使得这两个Token最高维的位置编码相同，而当a的底数设置为10000时，最高维的周期为，实际使用的时候，两个pos为整数的Token的位置编码碰撞的可能性就非常小了。

旋转位置编码

看到这里相信你已经对经典位置编码的由来有了一个初步的理解，后面我们理解旋转位置编码就不会太难了。

旋转位置编码的动机

在前面的经典位置编码中，我们是通过了在最开始的时候在Token的嵌入向量上直接添加的位置编码，公式表示为如下所示：

但这样做实际上引入了噪声，一方面它改变了嵌入的模长，另一方面在QKV的计算时，虽然引入了，但是同样也引入了以及 这样的噪声。

其次，由于只在最开始的时候加入了位置编码，这就使得位置信号在靠后的注意力层的计算中非常微弱。而旋转位置编码就是为了解决这两个问题而提出的。

针对噪声的优化

正如名称所言，旋转位置编码想到通过旋转的方式而不是叠加的方式来嵌入位置信息，这样嵌入向量的模长不变，只改变了嵌入向量的方向。

在二维中的旋转公式如下：

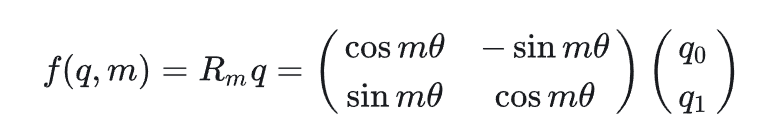
其中m为一个系数，θ为元角度，表示对向量q旋转了mθ度。

旋转天生就能反应这种角度之间的差值，而原先在经典位置编码中针对pos的位置编码我们是这样设置的：

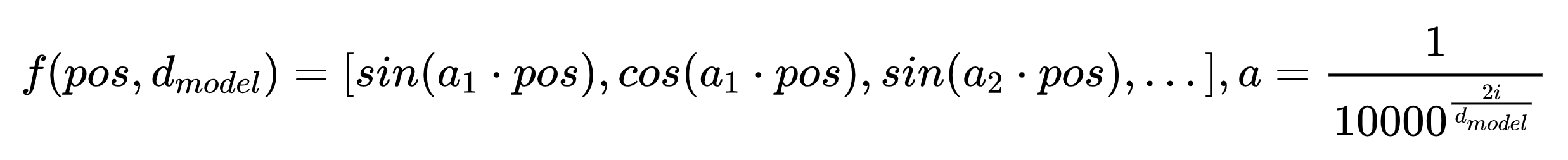
这里我们把m类比为pos, a类比为θ(之所以这么理解是因为在位置编码中，自变量是pos，我们是要建模pos与pos之间的关系，当然你可以把pos比作θ，a比作m, 这样反应的其实是同一个Token的位置编码时不同维度的位置编码的变化)，很容易想到，在经典位置编码中通过计算元角度a的pos倍得到的三角函数值来编码位置编码，在旋转矩阵中则应该对相同维度的嵌入进行旋转，而旋转的角度也为a的pos倍。注意这里的a是每两个值共用同一个a。

比如在嵌入只有两维的时候，编码位置信息可以采用以下公式得到：

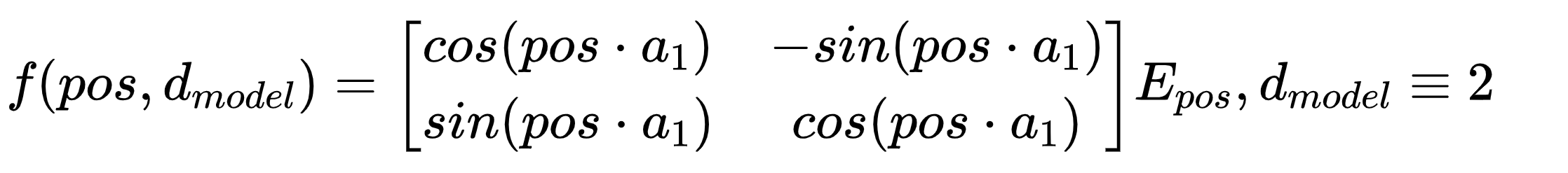
那么扩展到高维就是对每一维的数值进行旋转，旋转角是pos * a。

那么这样我们就得到了如下旋转矩阵：

为了在计算上进行优化，作者把旋转的计算写成了这种形式：

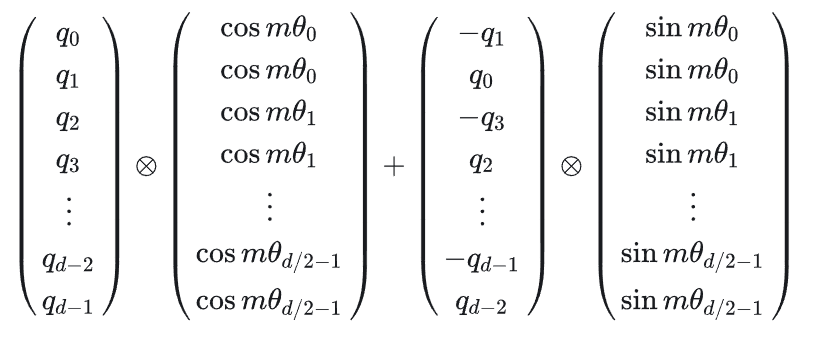
这就是原文中的公式由来。

针对信号减弱的优化

既然只在最开始做位置编码会导致信息传播减弱的问题，那就在每一次注意力的时候都做一次旋转即可，这样就能保留旋转的信息。

位置编码的实现

在我们之前的代码中，我们通过以下代码来应用旋转位置编码：

cos,sin = self.rotary_embedding(value_states,position_ids,seq_len = None) #不改变形状,这里value_states只是为了提供device
query_states,key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin)

但我们尚未实现它们，这里cos和sin主要就是构造了公式中的cos向量和sin向量,理解了原理之后我们的实现就很简单了：

首先实现cos,sin的向量构建：

class GemmaRotaryEmbedding(nn.Module): def __init__(self, dim:int, max_position_embeddings:int = 2048, base:int = 10000, device:torch.device = None):super().__init__()
		self.dim = dim
		self.base = base
		self.max_position_embeddings = max_position_embeddings# 计算公式 theta_i = base**(-(2i / dim)) ,i = 0,1,2,3.....dim // 2
		inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2).float() / self.dim))		self.register_buffer("inv_freq", inv_freq, persistent=False)def forward(self,x , position_ids:torch.Tensor, seq_len:Optional[int] = None):# x shape: [batch_size, num_attention_heads,seq_len, head_dim]		self.inv_freq = self.inv_freq.to(x.device) ##转移设备## 为后面的矩阵乘法做准备 inv_freq:[dim // 2] -> inv_freq_expanded: [batch_size, dim // 2, 1]
		inv_freq_expanded = self.inv_freq[None,:,None].float().expand(position_ids.shape[0],-1,1)## 为后面的矩阵乘法做准备 position_ids:[batch_size, seq_len] -> position_ids_expanded: [batch_size, 1, seq_len]
		position_ids_expanded = position_ids[:, None, :].float()		device_type = x.device.type
		device_type = device_type if isinstance(device_type,str) and device_type != "mps" else "cpu"with torch.autocast(device_type=device_type,enabled=False): ## 禁用自动混合精度## 这里是为了给每个不同位置的token准备一个m * theta, m代表position_id，由position_ids_expanded提供，theta_i 由inv_freq_expanded提供## [batch_size, dim // 2, 1] * [batch_size, 1, seq_len] = [batch_size, dim // 2, seq_len] -> [batch_size, seq_len, dim // 2] 
			freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1,2)## 将 dim // 2的 m * theta_i 扩展到dim维度，这里没有重复交替(m*θ 1,m*θ 1,m*θ 2,m*θ 2,...)是参照hugging face的实现，也能达到同样的效果
			emb = torch.cat((freqs,freqs),dim=-1)			cos = emb.cos()
			sin = emb.sin()return cos.to(dtype=x.dtype),sin.to(dtype=x.dtype)

这里可能比较疑惑的点在于这里的旋转位置编码为什么与论文不同，这是因为hugging face在导入模型的时候权重会发生置换，具体原因可以参考： 旋转位置编码差异详解 这里不过多赘述，大家只要知道原理就行。

那么至此我们完成了主模型的最后一块拼图。希望本文对各位理解位置编码有一些帮助。