条件扩散过程(附录H)
H 条件扩散过程
在本节中,我们表明,可以通过与 pθ(xt∣xt+1)pϕ(y∣xt)p_\theta(x_t|x_{t+1})p_\phi(y|x_t)pθ(xt∣xt+1)pϕ(y∣xt) 成比例的转移算子实现条件采样,其中 pθ(xt∣xt+1)p_\theta(x_t|x_{t+1})pθ(xt∣xt+1) 近似于 q(xt∣xt+1)q(x_t|x_{t+1})q(xt∣xt+1),而 pϕ(y∣xt)p_\phi(y|x_t)pϕ(y∣xt) 近似于带噪声样本 xtx_txt 的标签分布。
我们首先定义一个类似于 qqq 的条件马尔可夫噪声过程 q^\hat{q}q^,并假设对于每个样本,q^(y∣x0)\hat{q}(y|x_0)q^(y∣x0) 是已知且容易获得的标签分布。

虽然我们定义了在 yyy 条件下的噪声过程 q^\hat{q}q^,但我们可以证明,当不在 yyy 条件下时,q^\hat{q}q^ 的行为与 qqq 完全相同。沿着这些思路,我们首先推导无条件噪声算子 q^(xt+1∣xt)\hat{q}(x_{t+1}|x_t)q^(xt+1∣xt):
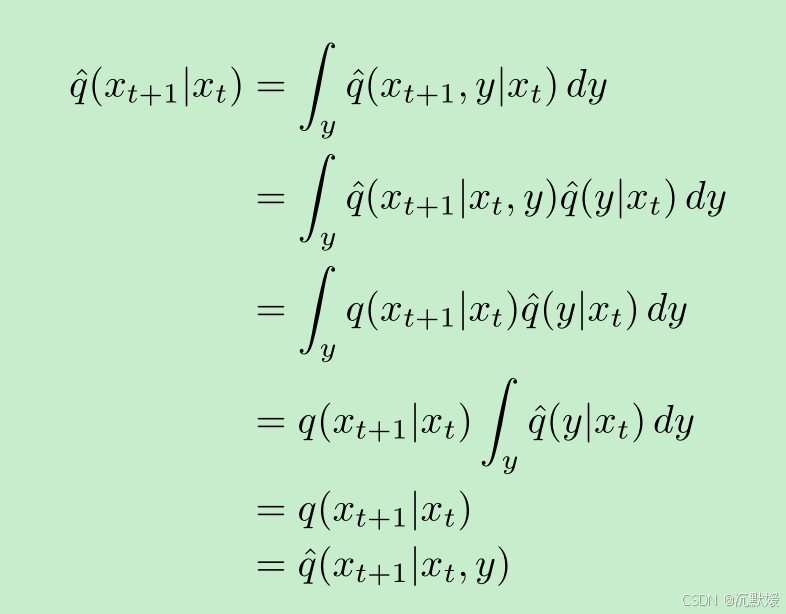
遵循类似的逻辑,我们得到联合分布 q^(x1:T∣x0)\hat{q}(x_{1:T}|x_0)q^(x1:T∣x0):
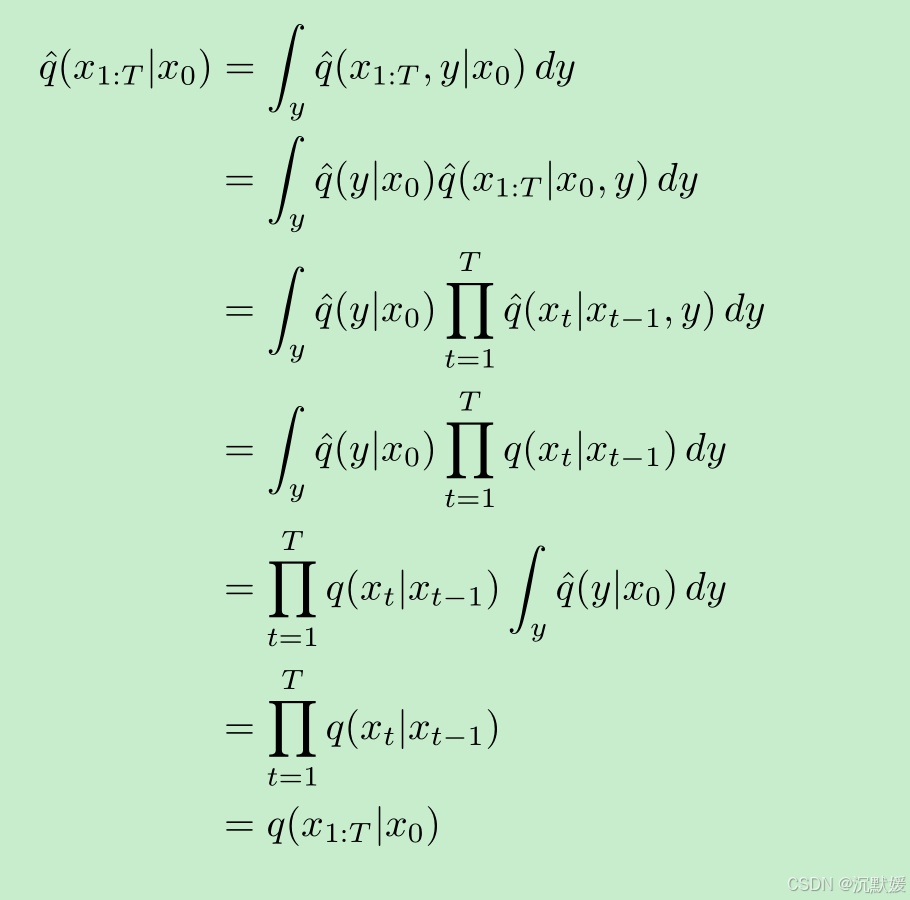
利用公式44,我们现在可以推导出 q^(xt)\hat{q}(x_t)q^(xt):
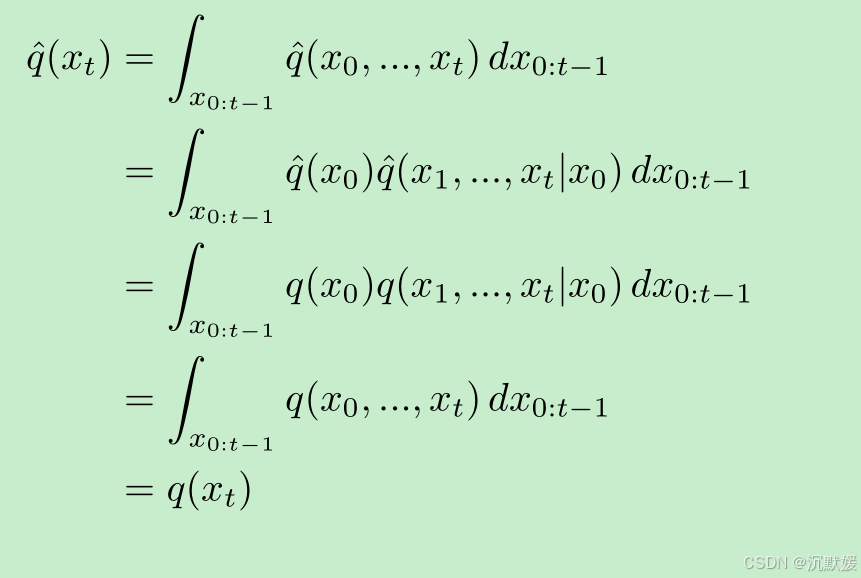
利用恒等式 q^(xt)=q(xt)\hat{q}(x_t)=q(x_t)q^(xt)=q(xt) 和 q^(xt+1∣xt)=q(xt+1∣xt)\hat{q}(x_{t + 1}|x_t)=q(x_{t + 1}|x_t)q^(xt+1∣xt)=q(xt+1∣xt),通过贝叶斯规则可以很直观地表明无条件反向过程 q^(xt∣xt+1)=q(xt∣xt+1)\hat{q}(x_t|x_{t + 1}) = q(x_t|x_{t + 1})q^(xt∣xt+1)=q(xt∣xt+1)。
关于 q^\hat{q}q^ 的一个观察结果是,它会产生一个含噪声的分类函数 q^(y∣xt)\hat{q}(y|x_t)q^(y∣xt)。我们可以证明,这个分类分布不依赖于 xt+1x_{t + 1}xt+1(xtx_txt 的一个更嘈杂版本),我们稍后将使用这一事实:
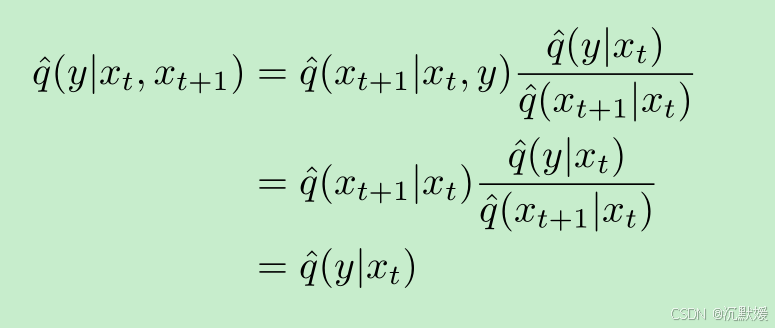
我们现在可以推导条件反向过程:
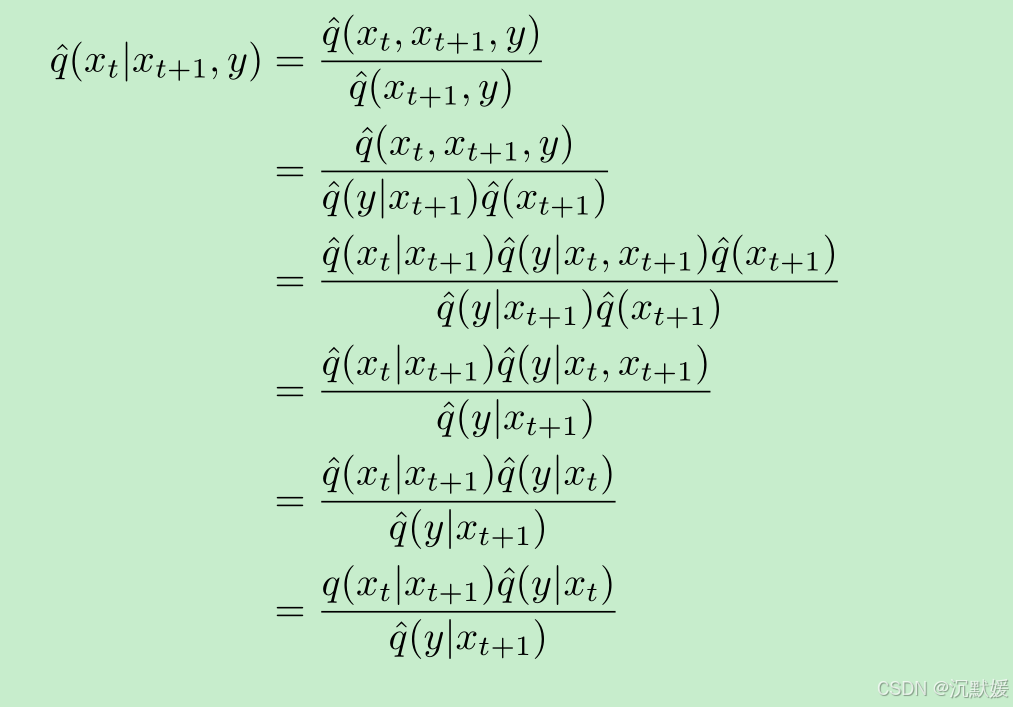
q^(y∣xt+1)\hat{q}(y|x_{t + 1})q^(y∣xt+1) 项可以视为常数,因为它不依赖于 xtx_txt。因此,我们希望从分布 Zq(xt∣xt+1)q^(y∣xt)Zq(x_t|x_{t + 1})\hat{q}(y|x_t)Zq(xt∣xt+1)q^(y∣xt) 中采样,其中 ZZZ 是归一化常数。我们已经有一个对 q(xt∣xt+1)q(x_t|x_{t + 1})q(xt∣xt+1) 的神经网络近似,称为 pθ(xt∣xt+1)p_{\theta}(x_t|x_{t + 1})pθ(xt∣xt+1),所以剩下的就是对 q^(y∣xt)\hat{q}(y|x_t)q^(y∣xt) 的近似。这可以通过在从 q(xt)q(x_t)q(xt) 采样得到的带噪声图像 xtx_txt 上训练分类器 pϕ(y∣xt)p_{\phi}(y|x_t)pϕ(y∣xt) 来实现。
