当前位置：首页 > news >正文

【不背八股】12.十大排序算法

news 2025/9/15 8:00:29

引言

通常被问到排序算法的时间复杂度，会对着下面这张表去查询。

算法	最好时间复杂度	最坏时间复杂度	稳定性
冒泡排序	O(n)	O(n²)	✅ 稳定
选择排序	O(n²)	O(n²)	❌ 不稳定
插入排序	O(n)	O(n²)	✅ 稳定
希尔排序	O(n log n)	O(n²)	❌ 不稳定
归并排序	O(n log n)	O(n log n)	✅ 稳定
快速排序	O(n log n)	O(n²)	❌ 不稳定
堆排序	O(n log n)	O(n log n)	❌ 不稳定
计数排序	O(n+k)	O(n+k)	✅ 稳定
桶排序	O(n)	O(n log n)	不确定
基数排序	O(n*m)	O(n*m)	✅ 稳定

稳定性是指：当待排序序列中存在相等元素时，排序后这些元素的相对顺序是否保持不变。

本文将更进一步，通过C++代码进一步分析，表中的数值是怎么来的，以加深对算法的理解。

1. 冒泡排序（Bubble Sort）

原理

通过不断比较相邻元素，如果前一个比后一个大，则交换。
每一轮“冒泡”都会把最大（或最小）的数移到数组的一端。

原理如下图[1]所示：

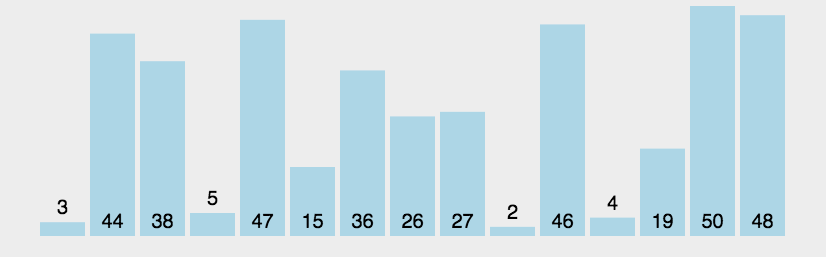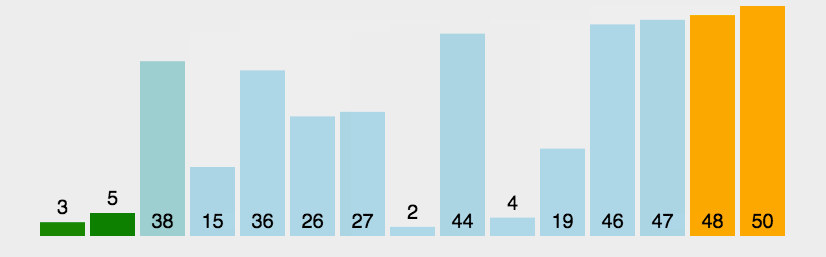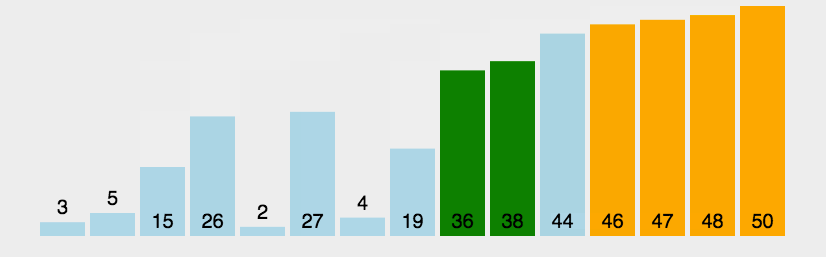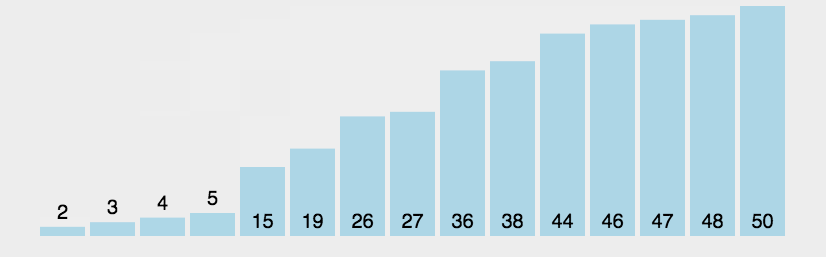
代码实现

void bubbleSort(vector<int>& arr) {int n = arr.size();bool swapped;for (int i = 0; i < n - 1; i++) {swapped = false;for (int j = 0; j < n - 1 - i; j++) {if (arr[j] > arr[j+1]) {swap(arr[j], arr[j+1]);swapped = true;}}if (!swapped) break; // 提前结束}
}

最好的情况：数组已排好序，那么swapped一直为false，相当于一轮中不需要交换，遍历一次数组就行了，因此时间复杂度是 O(n)。

最坏的情况：数组完全逆序，每一轮冒泡都需要交换，时间复杂度是O(n²)。

稳定情况具体要看代码，比如上面标准写法的交换条件是arr[j] > arr[j+1]，说明两个数相等的情况下不会发生交换，因此是稳定的。反之，如果写成了arr[j] >= arr[j+1]，则是不稳定的。

2 选择排序（Selection Sort）

原理

每一轮从未排序部分中选择最小的元素，放到已排序部分的末尾。

原理如下图[1]所示：

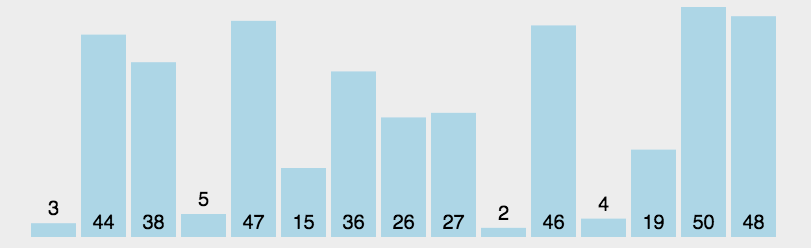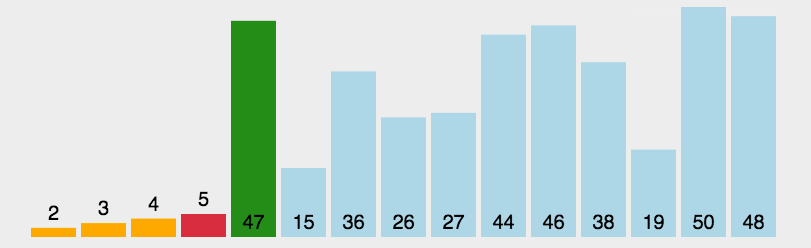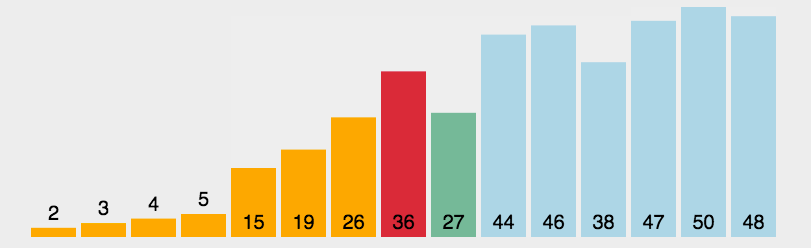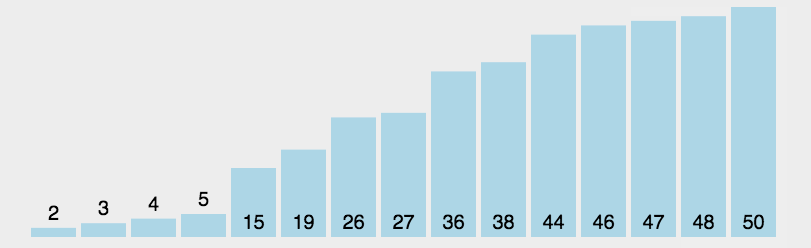
代码实现

void selectionSort(vector<int>& arr) {int n = arr.size();for (int i = 0; i < n - 1; i++) {int minIndex = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}swap(arr[i], arr[minIndex]);}
}

无论初始数组是顺序还是逆序，选择排序都需要进行两轮迭代，因此时间复杂度都是O(n²)。

由于选择排序每轮交换是将当前值和后面的最小值进行交换，因此有可能会把前面的值移动到后面去，因此是不稳定的。

3. 插入排序（Insertion Sort）

原理

类似于整理扑克牌：将当前元素插入到前面已经有序的部分。

原理如下图[1]所示：

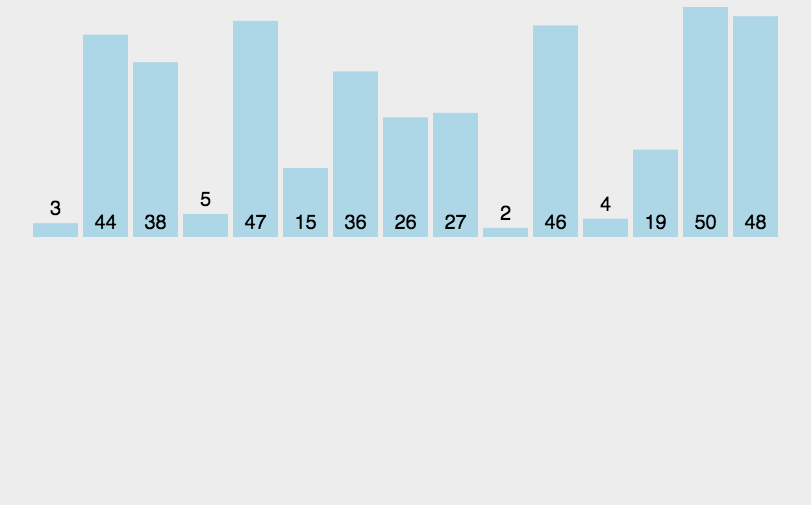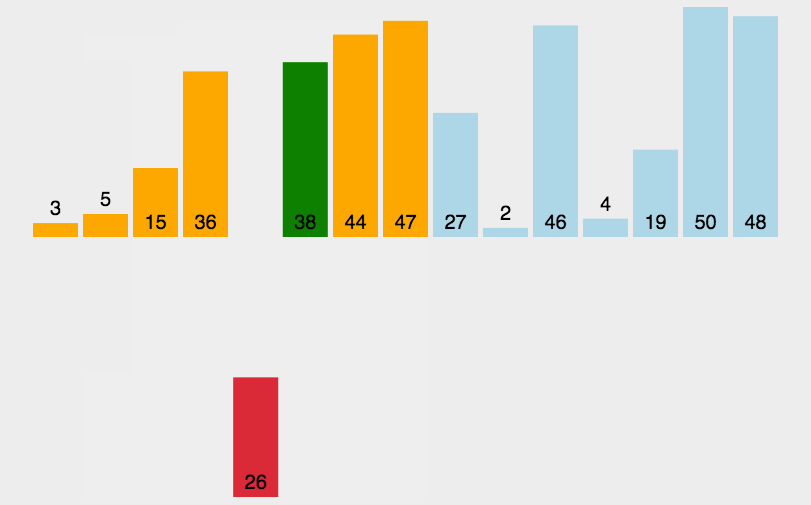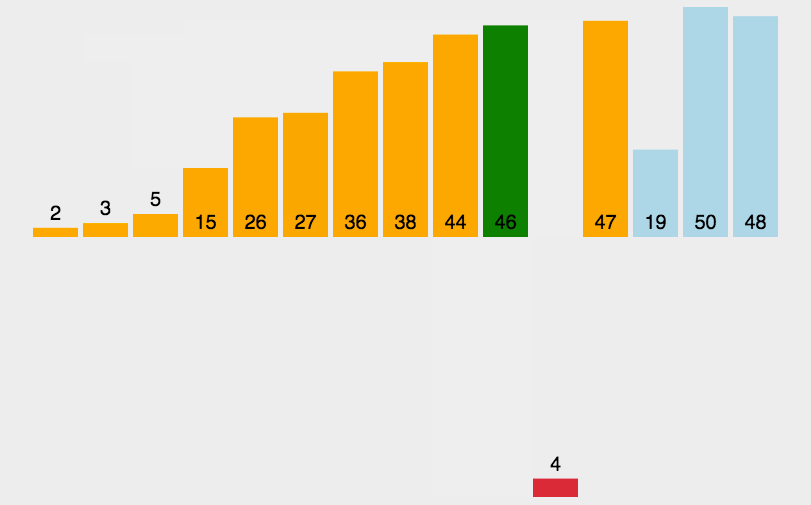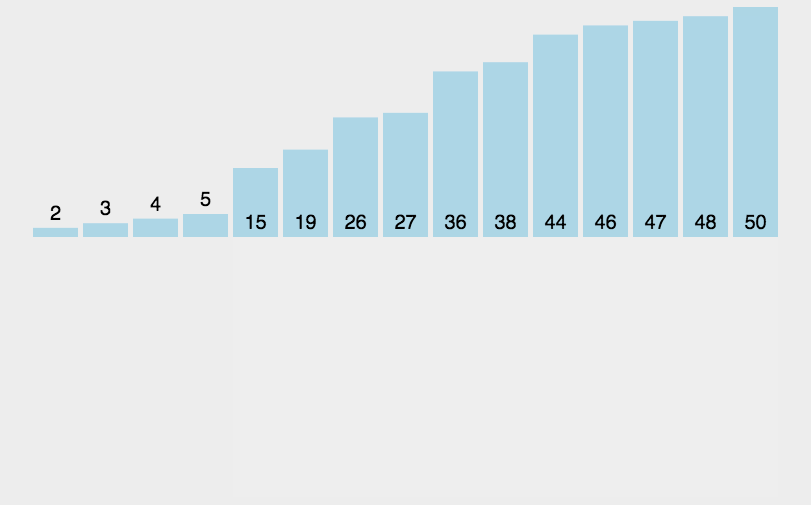
代码实现

void insertionSort(vector<int>& arr) {int n = arr.size();for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j+1] = arr[j];j--;}arr[j+1] = key;}
}

时间复杂度和冒泡排序有点类似，最好的情况（数组基本有序），直接并到已排完序的后面就行了，时间复杂度是O(n)。

最坏的情况，数组完全逆序，每次都需要查到最开头，因此时间复杂度是O(n²)。

两数相等情况下，后面的数默认会插入到前一个数的后面，顺序不变，因此是稳定的。

4. 希尔排序（Shell Sort）

原理

希尔排序是插入排序的改进版。
核心思想：先选取一个间隔 gap，将数组分为多个子序列，对每个子序列进行插入排序；逐步缩小 gap，直到 gap=1 时完成排序。
这样能让元素更快接近目标位置，减少移动次数。

原理如下图[1]所示：

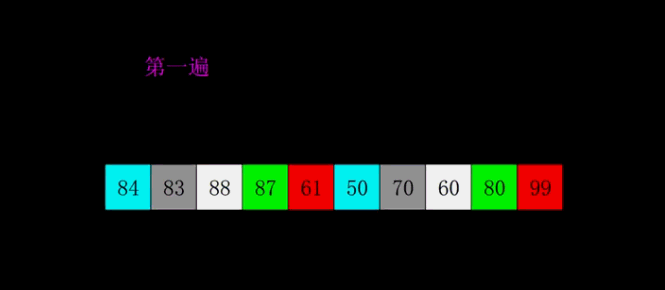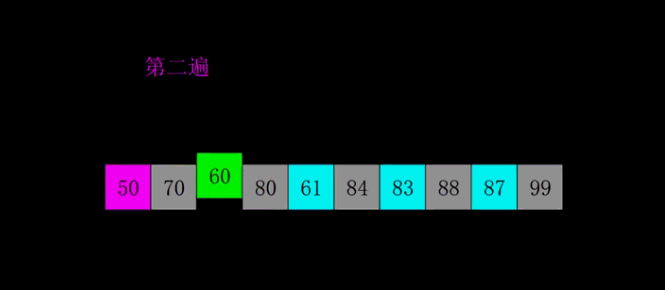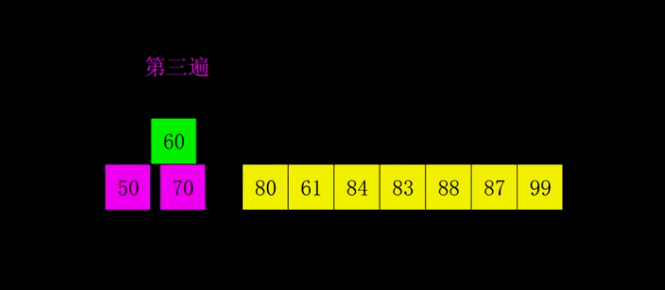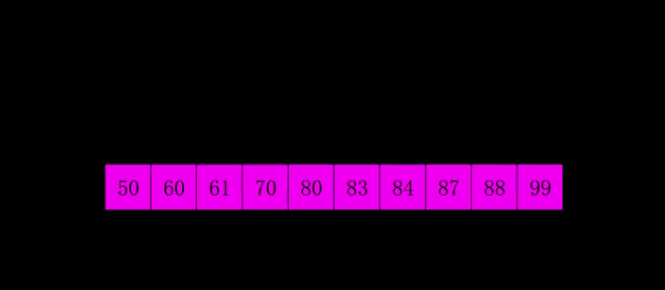
代码实现

void shellSort(vector<int>& arr) {int n = arr.size();for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j = i;while (j >= gap && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}}
}

gap 每次都缩小一半(n/2, n/4, n/8, ..., 1)，总共要做 log n 轮子序列插入排序。最好的情况下，时间复杂度是O(n log n)。

最坏的情况，数组完全逆序，时间复杂度和插入排序一样，退化到O(n²)。

元素会跨越多个 gap 进行比较和交换，可能导致相等元素的相对顺序被打乱，因此该算法不是稳定的。

5. 归并排序（Merge Sort）

原理

分治思想：递归地将数组一分为二，直到无法再分；
然后将两个有序子数组归并成一个更大的有序数组；
归并时使用额外空间存储中间结果。

原理如下图[1]所示：

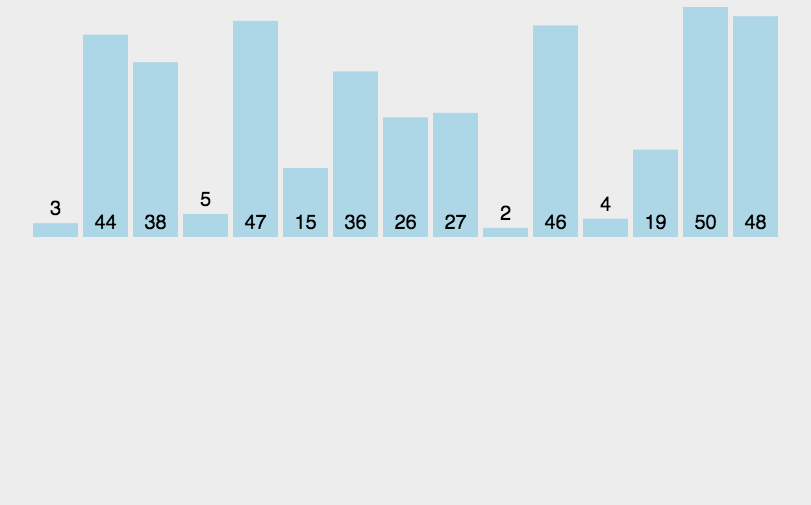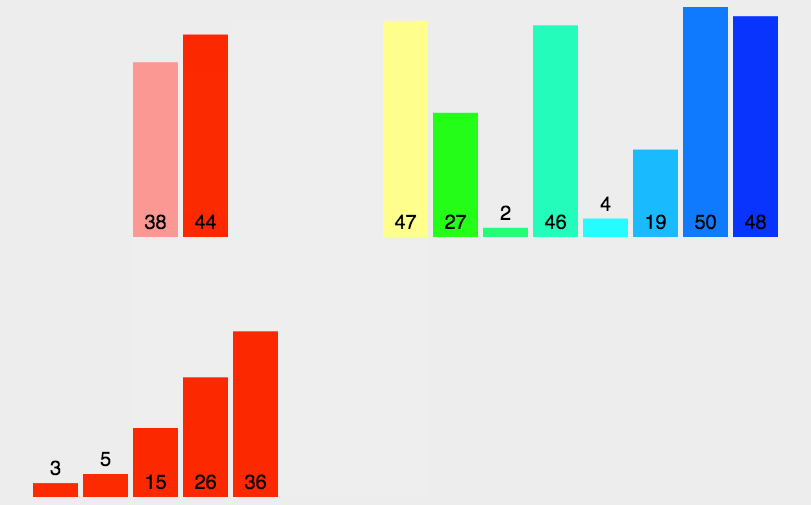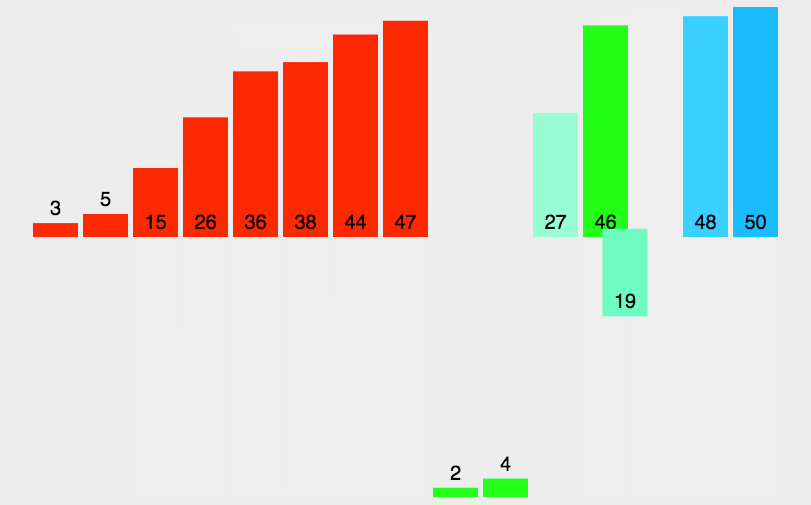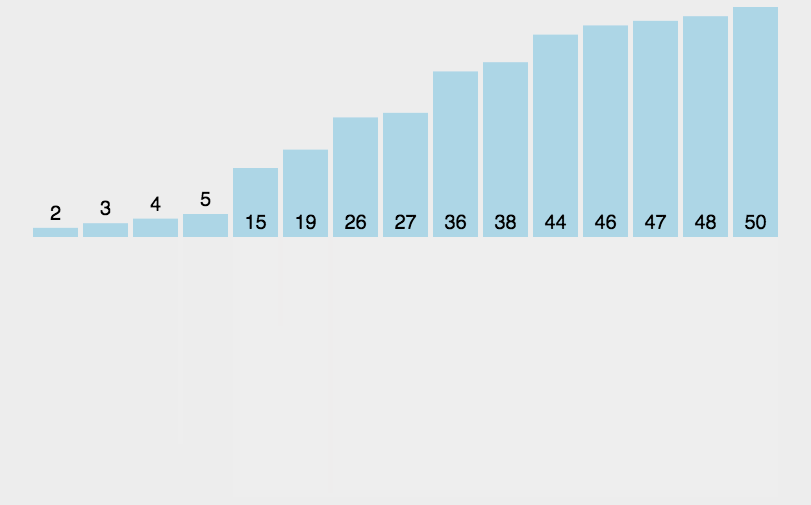
代码实现

void merge(vector<int>& arr, int left, int mid, int right) {int n1 = mid - left + 1;int n2 = right - mid;vector<int> L(n1), R(n2);for (int i = 0; i < n1; i++) L[i] = arr[left + i];for (int j = 0; j < n2; j++) R[j] = arr[mid + 1 + j];int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) arr[k++] = L[i++];else arr[k++] = R[j++];}while (i < n1) arr[k++] = L[i++];while (j < n2) arr[k++] = R[j++];
}void mergeSort(vector<int>& arr, int left, int right) {if (left >= right) return;int mid = left + (right - left) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);
}

归并排序和选择排序有点类似，不管数组乱序还是逆序，都需要进行从小到大的流程化操作，因此时间复杂度都是O(n log n)，log n 来源于分解过程，每次都是一分为二。

归并排序对每个数在局部进行操作，因此是稳定的。

6. 快速排序（Quick Sort）

原理

分治思想：选择一个“基准元素”（pivot），将数组分成两部分：小于 pivot 和大于 pivot；
分别对两部分递归排序；
不需要额外数组（就地分区）。

原理如下图[1]所示：

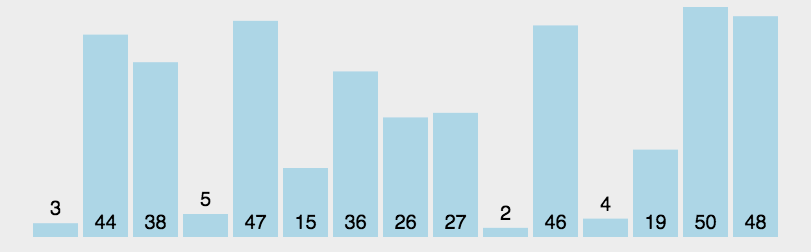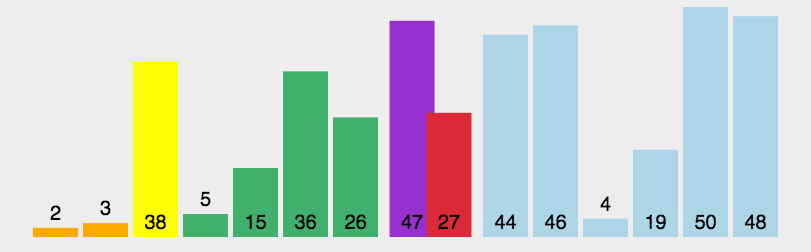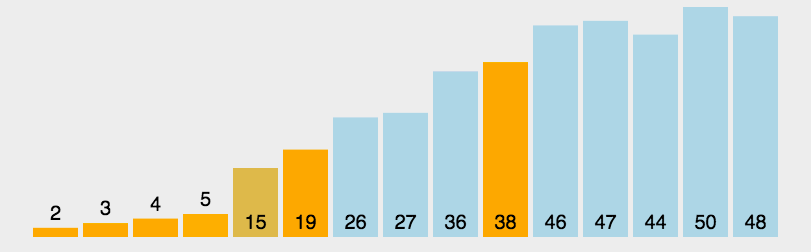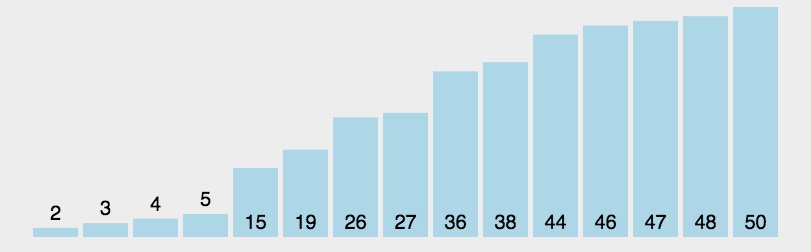
代码实现

int partition(vector<int>& arr, int low, int high) {int pivot = arr[high]; // 选择最后一个元素为基准int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;swap(arr[i], arr[j]);}}swap(arr[i+1], arr[high]);return i+1;
}void quickSort(vector<int>& arr, int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}

最好情况是，每次选取的pivot 都能恰好将数组均分成两半，时间复杂度是 O(n log n)。

最好情况是，数组完全顺序或者逆序，选取pivot是最大值或最小值，反而让计算变得更多，时间复杂度退化成 O(n²)。

pivot 左右两边的元素可能会跨区间交换，导致相等元素的相对顺序被打乱，因此算法是不稳定的。

7. 堆排序（Heap Sort）

原理

基于 堆（Heap） 的选择排序。
先将数组构造成一个 最大堆；
每次取出堆顶元素（最大值），与堆尾交换，然后重新调整堆；
直到堆的大小缩减为 1，排序完成。

原理如下图[1]所示：

代码实现

void heapify(vector<int>& arr, int n, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < n && arr[left] > arr[largest]) largest = left;if (right < n && arr[right] > arr[largest]) largest = right;if (largest != i) {swap(arr[i], arr[largest]);heapify(arr, n, largest);}
}void heapSort(vector<int>& arr) {int n = arr.size();// 构建最大堆for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 逐个取出堆顶元素for (int i = n - 1; i > 0; i--) {swap(arr[0], arr[i]);heapify(arr, i, 0);}
}

无论是顺序还是逆序，都需要建堆：O(n)，每次堆化：O(log n)，时间复杂度就是O(n log n)。

因为堆化过程中可能交换相同元素的相对顺序，因此算法是不稳定的。

8. 计数排序（Counting Sort）

原理

适合整数排序，且数据范围不大时效果最好。
统计每个数出现的次数，再累加得到位置，然后将数据放回原数组。

原理如下图[1]所示：

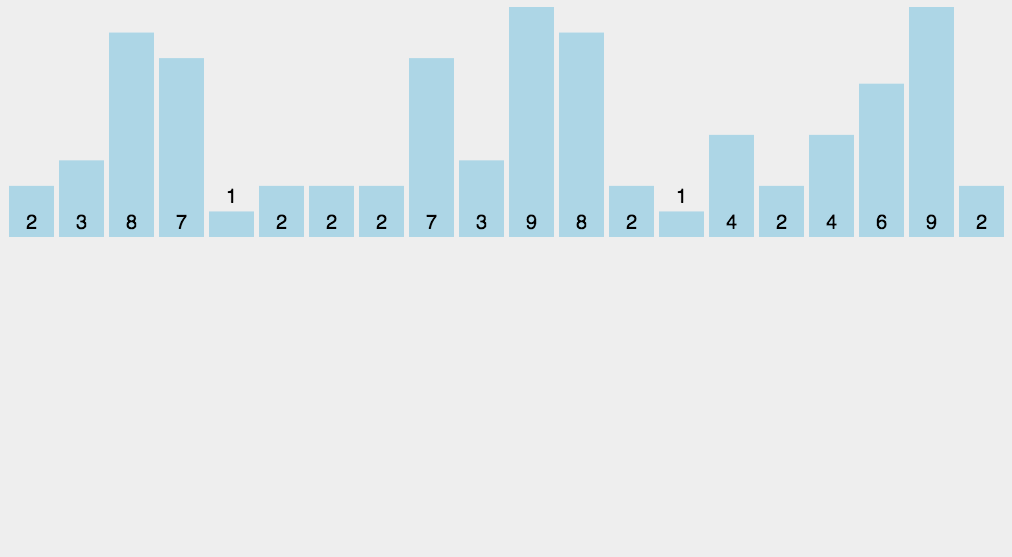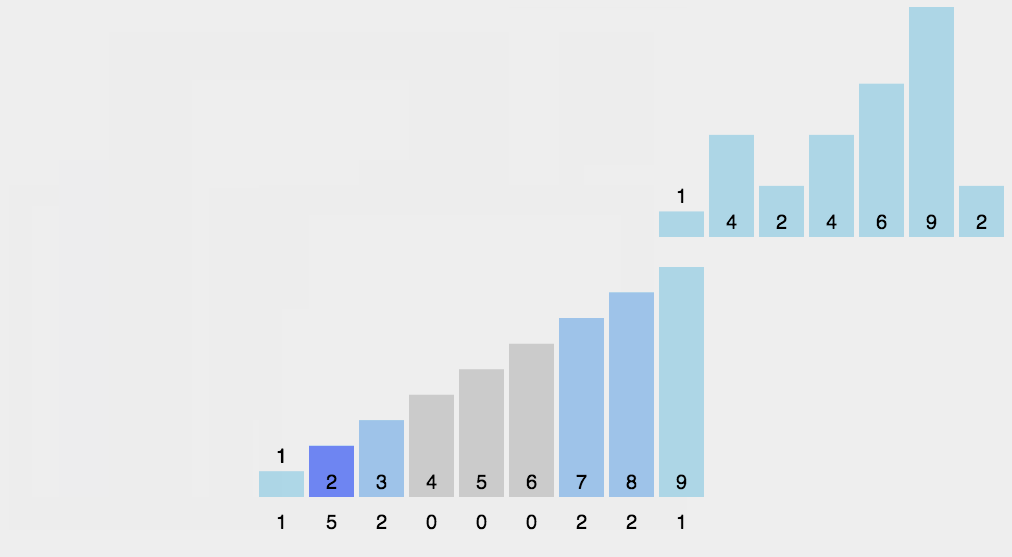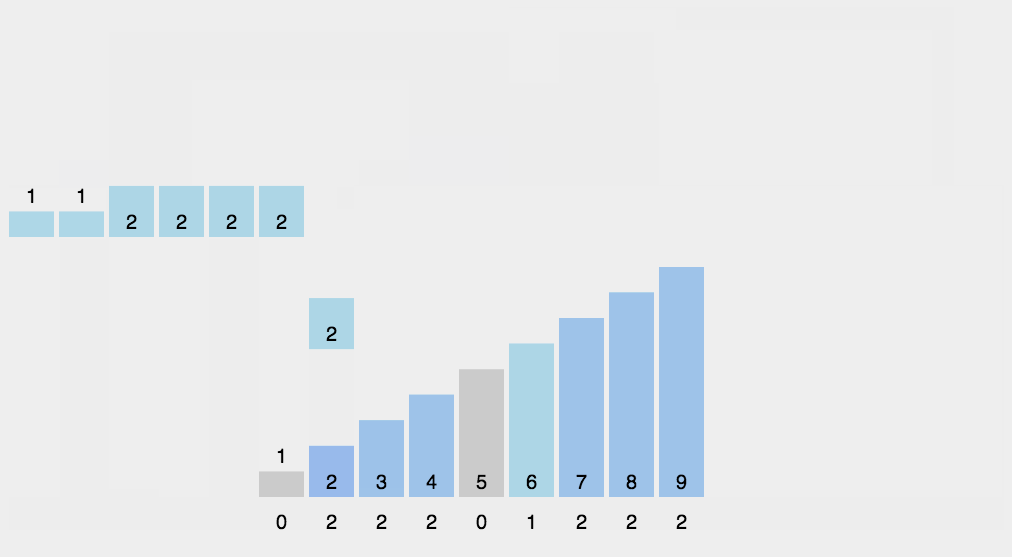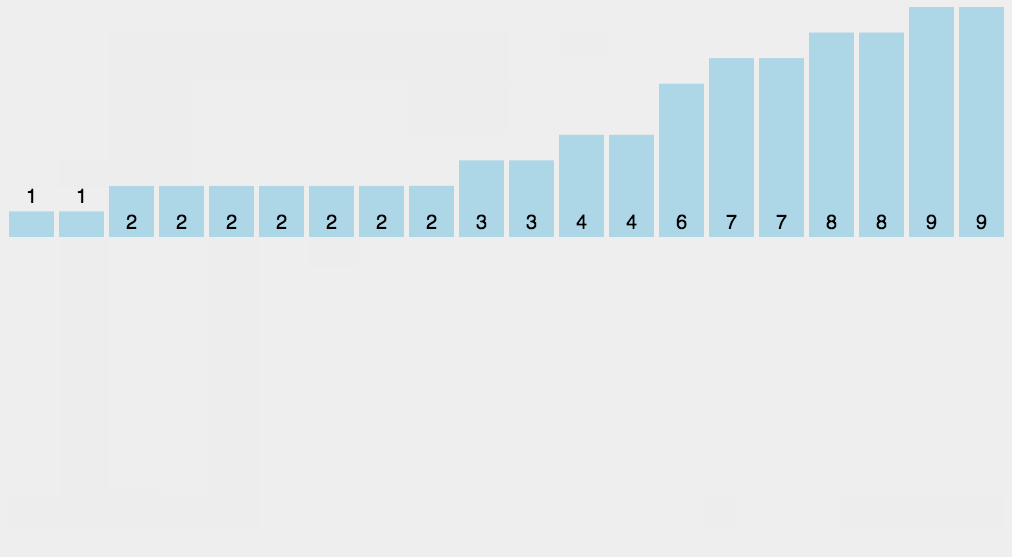
代码实现

void countingSort(vector<int>& arr) {if (arr.empty()) return;int maxVal = *max_element(arr.begin(), arr.end());int minVal = *min_element(arr.begin(), arr.end());int range = maxVal - minVal + 1;vector<int> count(range, 0);vector<int> output(arr.size());for (int num : arr) count[num - minVal]++;for (int i = 1; i < range; i++) count[i] += count[i - 1];for (int i = arr.size() - 1; i >= 0; i--) {output[count[arr[i] - minVal] - 1] = arr[i];count[arr[i] - minVal]--;}arr = output;
}

这个算法的时间上限取决于额外构建的计数器数组，该数组的上限取决于原数组的数值范围(最小值-最大值，记为k）,因此，无论什么情况，都需要遍历原数组+计数器数组，时间复杂度是O(n + k)。

排序后，不改变相同值得顺序，因此该算法是稳定的。

9. 桶排序（Bucket Sort）

原理

将数据分配到若干“桶”中，每个桶再单独排序；
最后将桶内数据依次合并。
当输入数据 分布均匀 时效率极高。

原理如下图[2]所示：

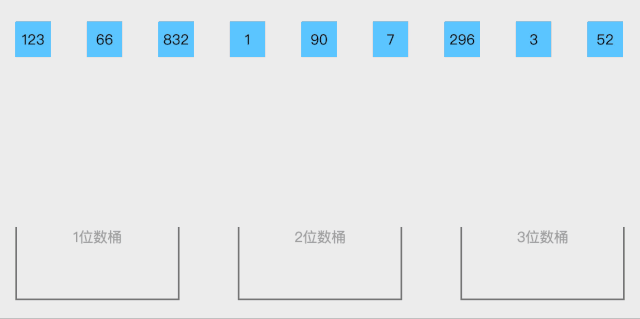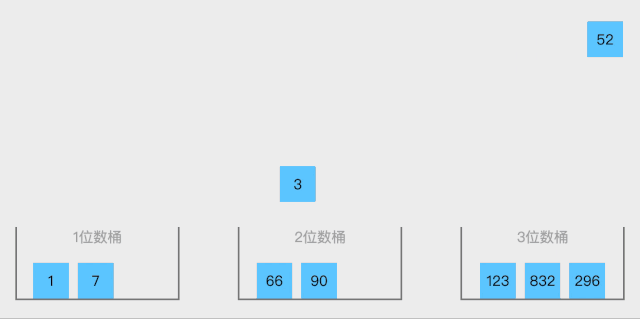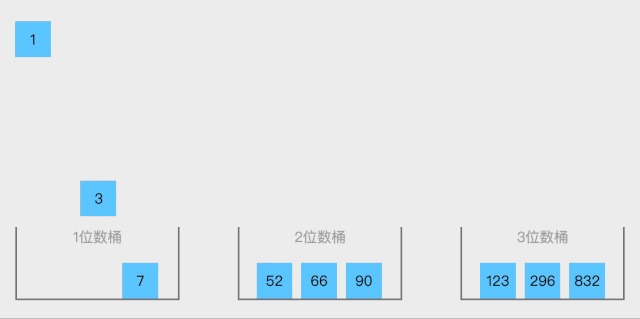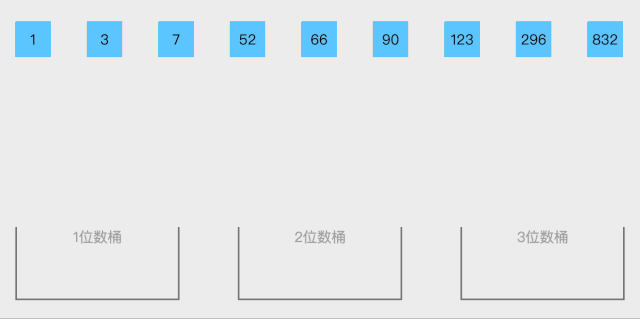
代码实现

void bucketSort(vector<int>& arr) {if (arr.empty()) return;int n = arr.size();int maxVal = *max_element(arr.begin(), arr.end());int minVal = *min_element(arr.begin(), arr.end());int bucketCount = n;vector<vector<int>> buckets(bucketCount);for (int num : arr) {int idx = (num - minVal) * (bucketCount - 1) / (maxVal - minVal);buckets[idx].push_back(num);}arr.clear();for (auto& bucket : buckets) {sort(bucket.begin(), bucket.end()); // 桶内排序，可换插入排序arr.insert(arr.end(), bucket.begin(), bucket.end());}
}

代码中，每个桶的范围和动图演示中略有差异。

假设数组：arr = [12, 15, 20, 35, 40, 55]

minVal = 12, maxVal = 55, n = 6;

每个桶的宽度 ≈ $(55 - 12) / (6 - 1) = 43/5 \approx 8.6$

最好情况，数据分布均匀，时间复杂度为O(n)。

最坏情况，数据极度不均匀，大部分元素都落在同一个桶里，相当于直接用其它排序算法对桶进行排序，比如代码里用的是sort，则时间复杂度是O(n log n)。

算法的稳定性取决于桶内排序算法，因此是不确定的。

10. 基数排序（Radix Sort）

原理

按 个位、十位、百位… 逐位进行排序；
每次排序使用 稳定的排序算法（如计数排序）。
常用于大整数排序。

原理如下图[1]所示：

代码实现

void countingSortByDigit(vector<int>& arr, int exp) {int n = arr.size();vector<int> output(n);vector<int> count(10, 0);for (int num : arr) count[(num / exp) % 10]++;for (int i = 1; i < 10; i++) count[i] += count[i - 1];for (int i = n - 1; i >= 0; i--) {int digit = (arr[i] / exp) % 10;output[count[digit] - 1] = arr[i];count[digit]--;}arr = output;
}void radixSort(vector<int>& arr) {int maxVal = *max_element(arr.begin(), arr.end());for (int exp = 1; maxVal / exp > 0; exp *= 10)countingSortByDigit(arr, exp);
}