Games101 第七章 几何

隐式几何

没有直接给出点的位置

公式描述

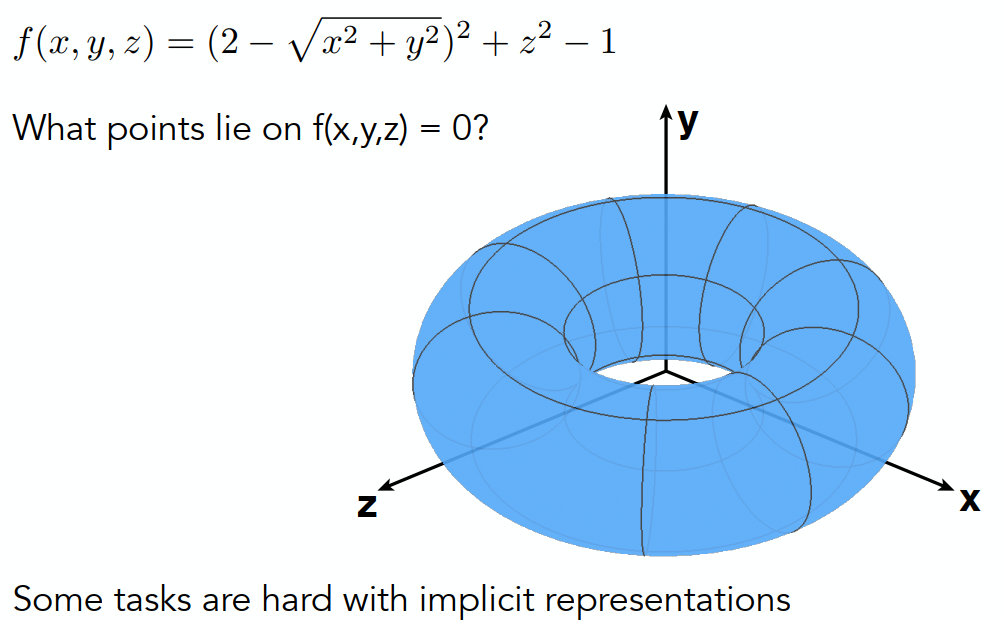
优点，容易判断点是在几何图形里面还是外面。

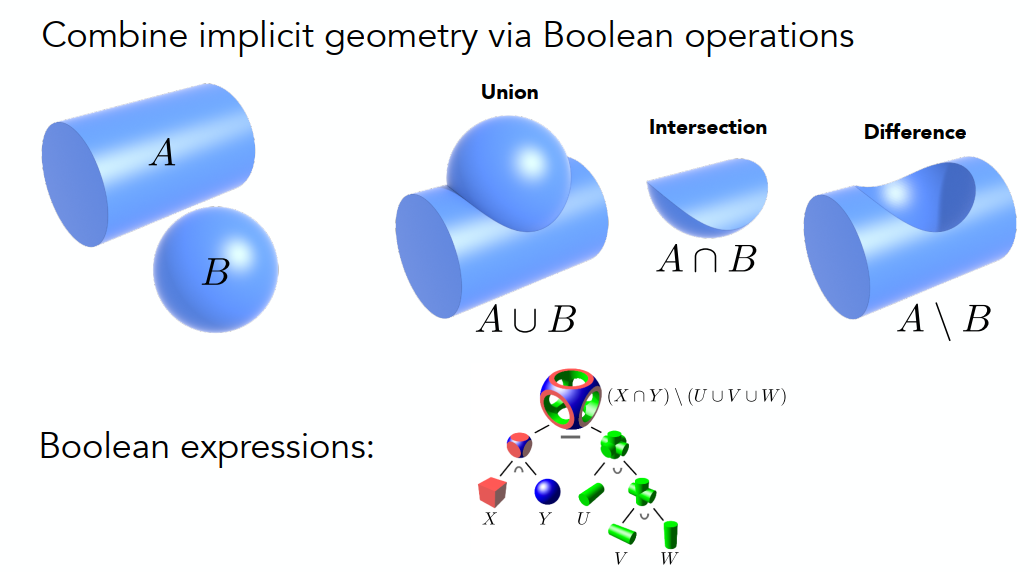
构造性立体几何（Constructive Solid Geometry ）

用简单的几何组合表示：

距离函数

在距离函数中，几何边界为0，向内为负，向外为正

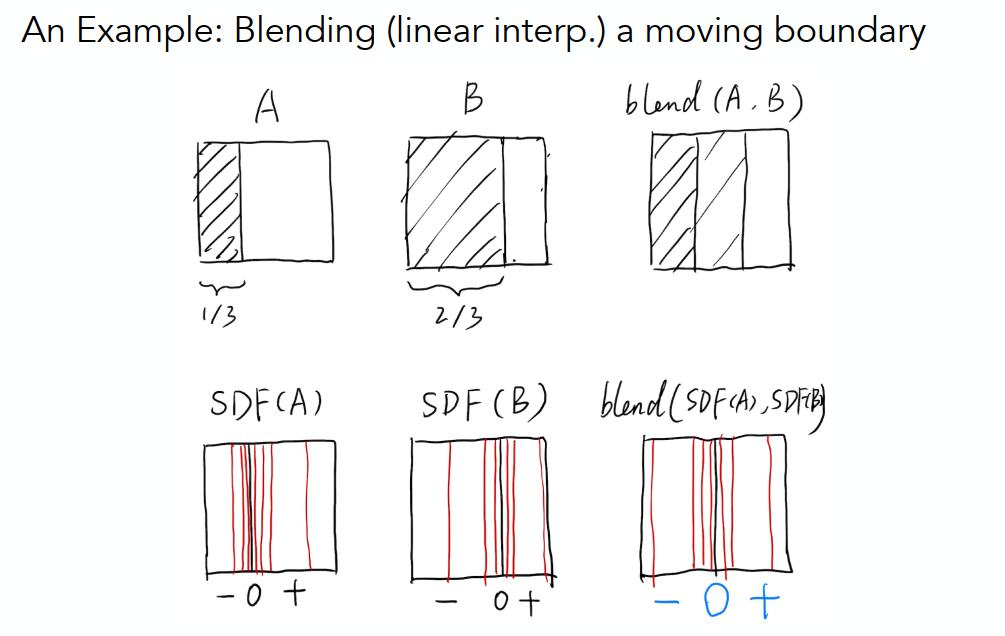
将距离函数混合时（blend），将两者直接相加，即可得到中间混合形态。

水平集（Level Set Methods ）

方程很难描述复杂情况，作为一种代替方案，水平集用网格存储近似的距离值。

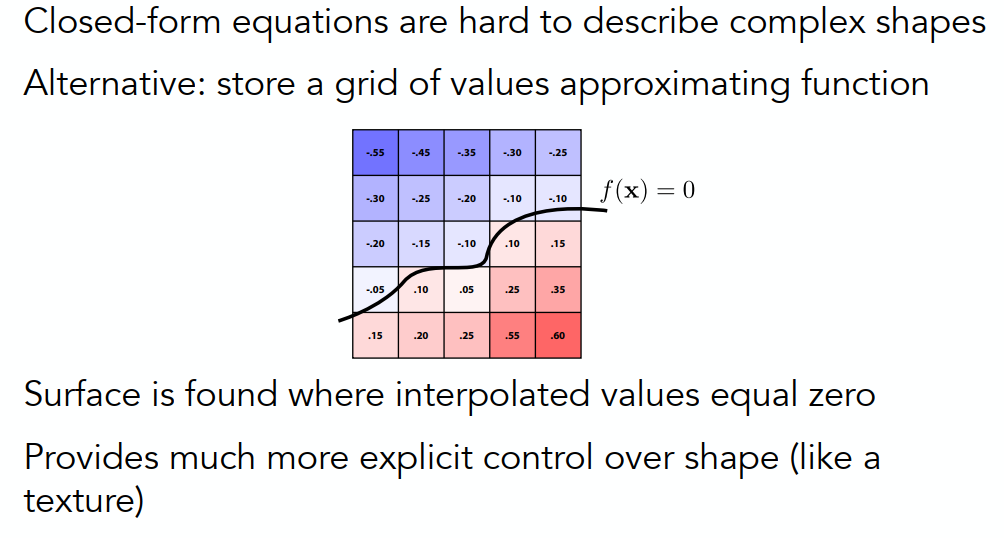
分形（Fractals ）

显式几何

所有的点都给出或者通过参数映射给出

参数映射（二维到三维）

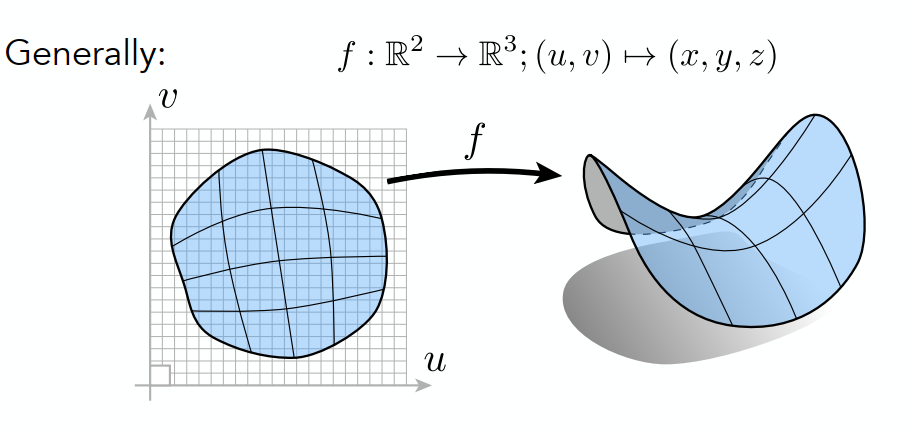
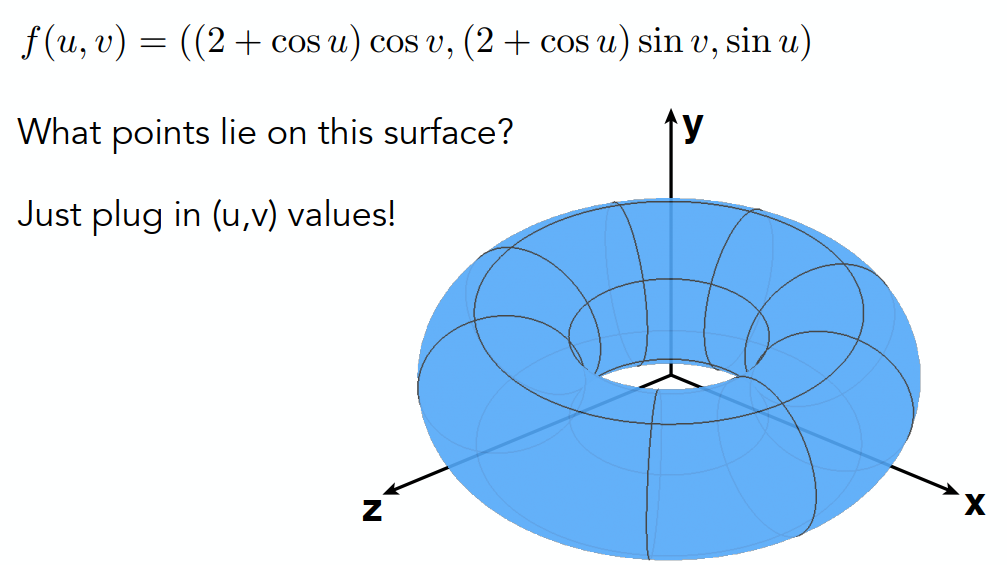
缺点：难以判断点在图形的内外。

点云

对物体表面采样得到的点：

网格

网格的表示方式：
.obj文件的表示方式：本质上是一个文本。
以下以一个正方体的表示为例

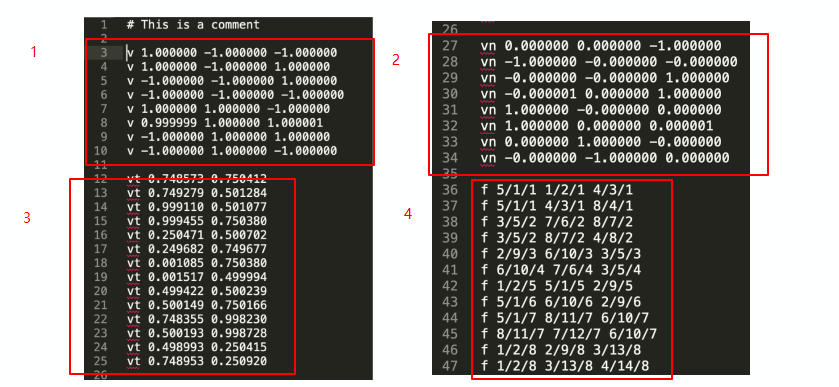
1. 表示的是组成组成正方体的8个点
2. 表示是6个法线（这里有些重复的行）
3. 表示的是纹理坐标表（uv）
4. 表示的是每个面的信息，在一行三组向量中：每组向量的第一个值代表了每个三角面顶点的编号，第二个值代表了顶底处的法线坐标编号，第三个值代表了该面的法向量编号。

曲线

贝塞尔曲线

下面一组图是贝塞尔曲线生成的原理：




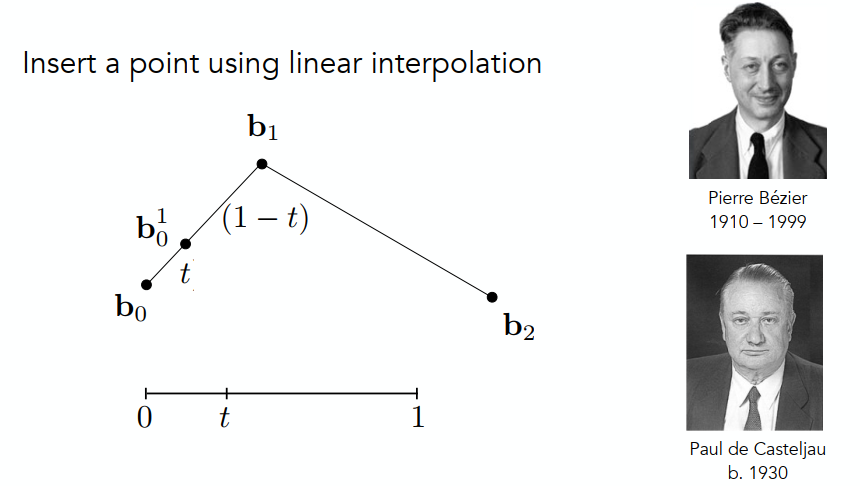
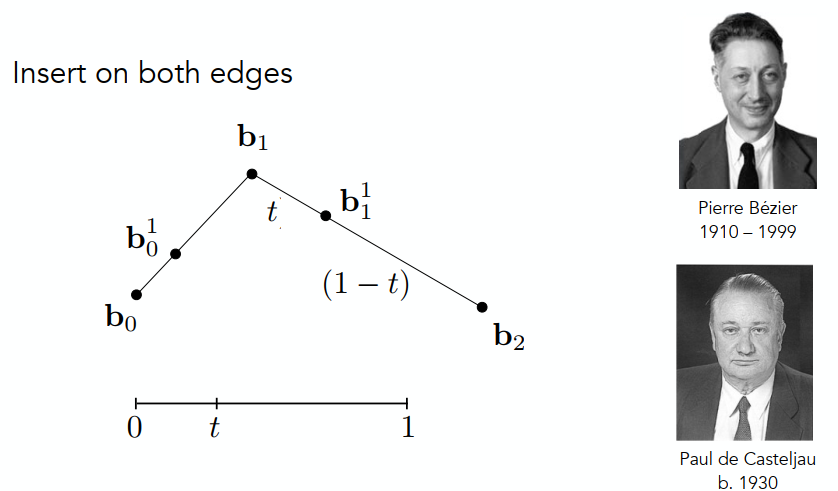
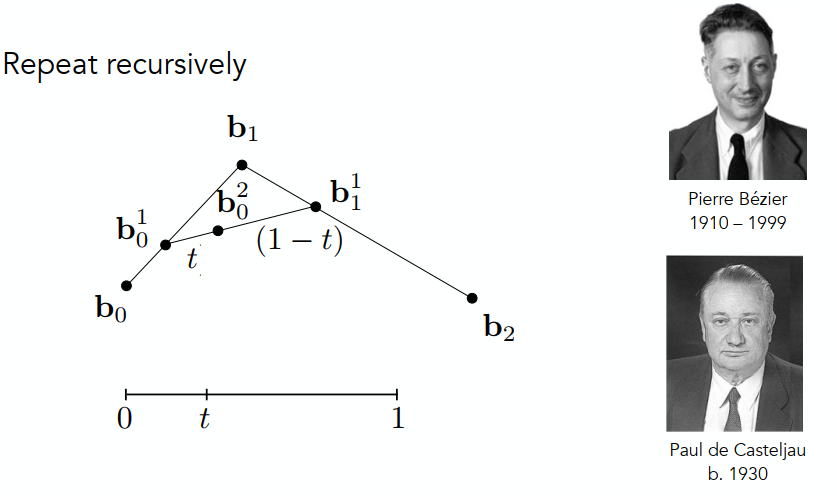
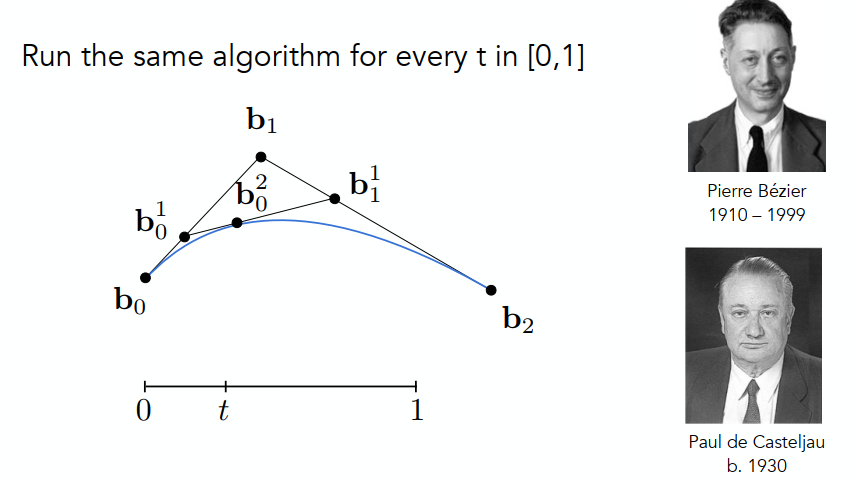
四个基点产生贝塞尔曲线的方法类似：

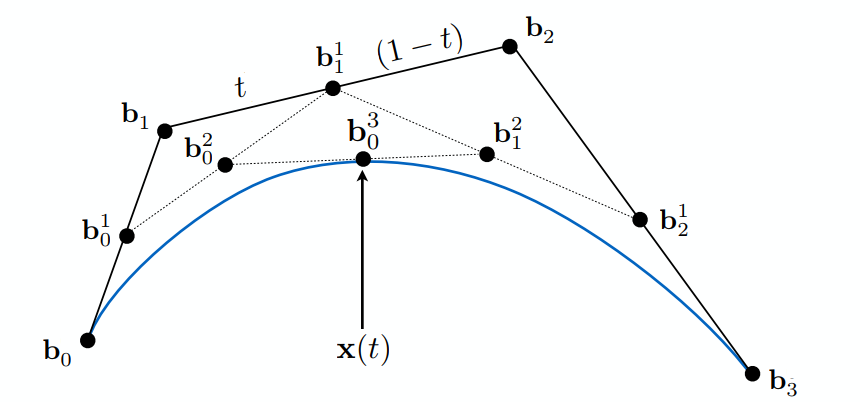
Casteljau算法

上图是三个点二维贝塞尔曲线的表示：贝塞尔曲线任意一点可以转化为基点的表示。

n维贝塞尔曲线的表示方式，这里的系数项$B_i^n(t)$是关于$t$和$1-t$的二项式。
这是一个三维贝塞尔曲线的例子：

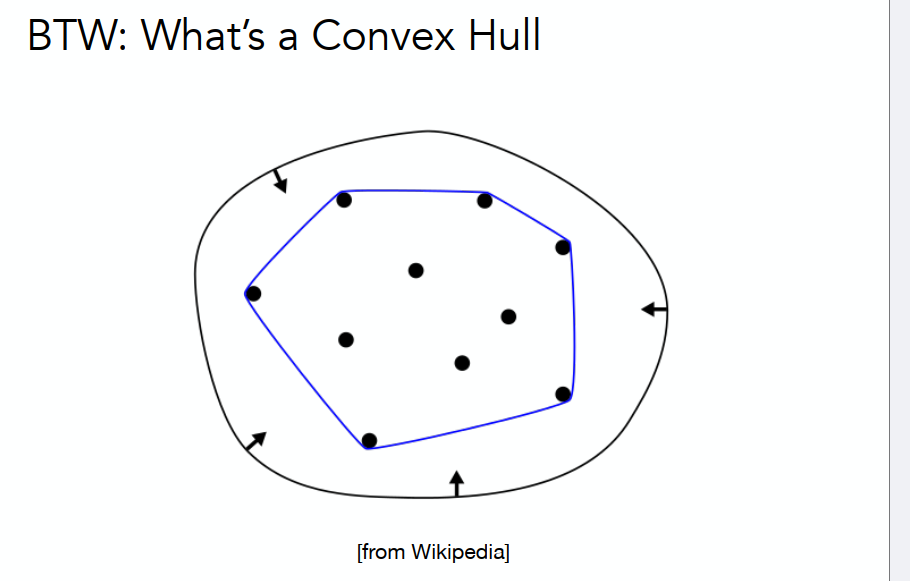
贝塞尔曲线的性质：

贝塞尔曲线总在基点的包围和内

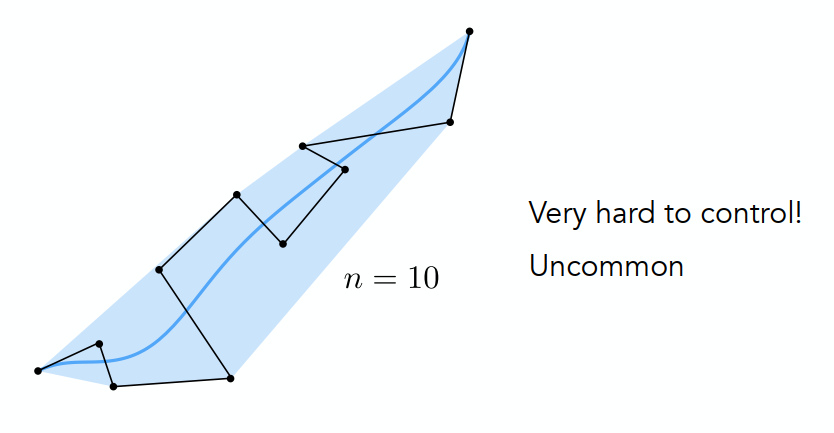
分段贝塞尔曲线

在工程上我们一般用分段贝塞尔曲线代替多点贝塞尔

多点贝塞尔的连接

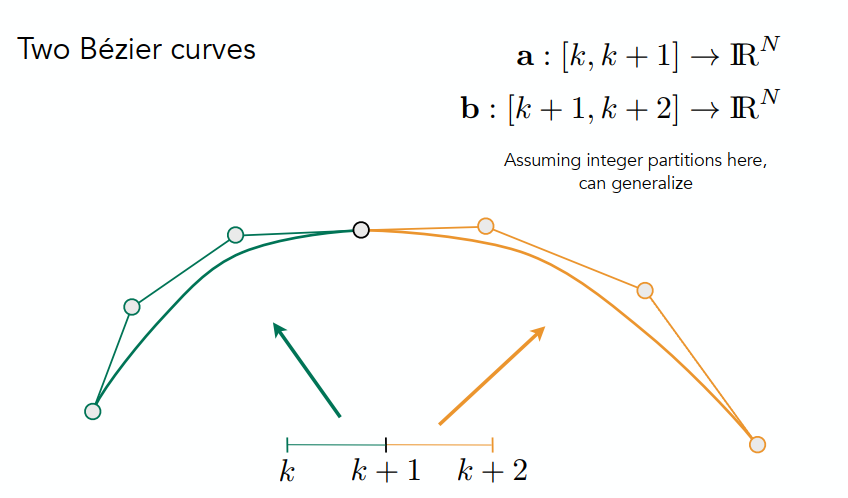
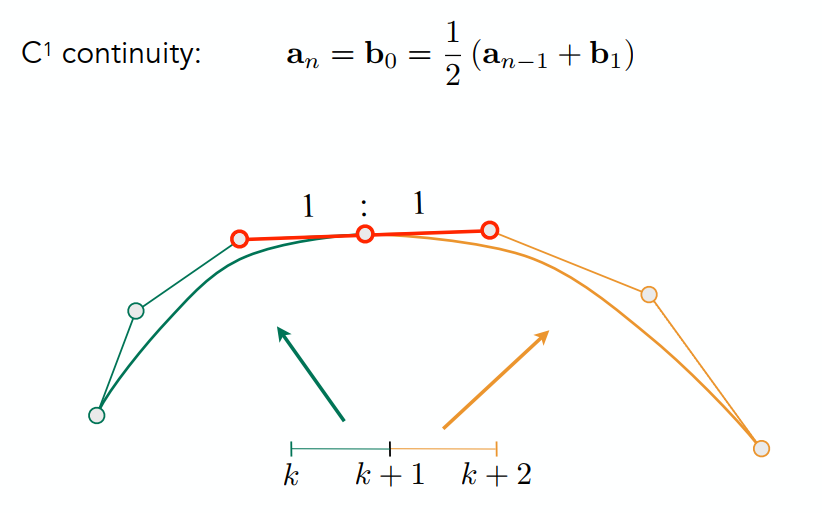
$a$代表第一个贝塞尔曲线，$b$代表第二个贝塞尔曲线

样条

以前用在不同点固定树枝的方式，来画曲线，这被称为样条。现在计算机也用这种方式画曲线。

B样条
在贝塞尔曲线的基础上改进，具有局部调整的能力，更加灵活。
NURBS
更加复杂的B样条。