【记录】初赛复习 Day1
我自己复习初赛的记录,是这个网站:
信息学奥赛-NOIP-少儿编程培训-有道小图灵 (youdao.com)里面的电子讲义
1.小数转二进制短乘法

2.原码补码反码

3.阅读程序 1
#include <iostream>
using namespace std;long long n, ans;
int k, len;
long long d[1000000];int main() {cin >> n >> k;d[0] = 0;len = 1;ans = 0;for (long long i = 0; i < n; ++i) {++d[0];for (int j = 0; j + 1 < len; ++j) {if (d[j] == k) {d[j] = 0;d[j + 1] += 1;++ans;}}if (d[len - 1] == k) {d[len - 1] = 0;d[len] = 1;++len;++ans;}}cout << ans << endl;return 0;
}
这个程序如果输入 n > 1 和 k = 1,len 是恒为 2 的,输出恒为 n。
我感觉还是挺难的,等差数列求和公式要不是刚复习过,就不会用了。
4.2 的相关进制转换
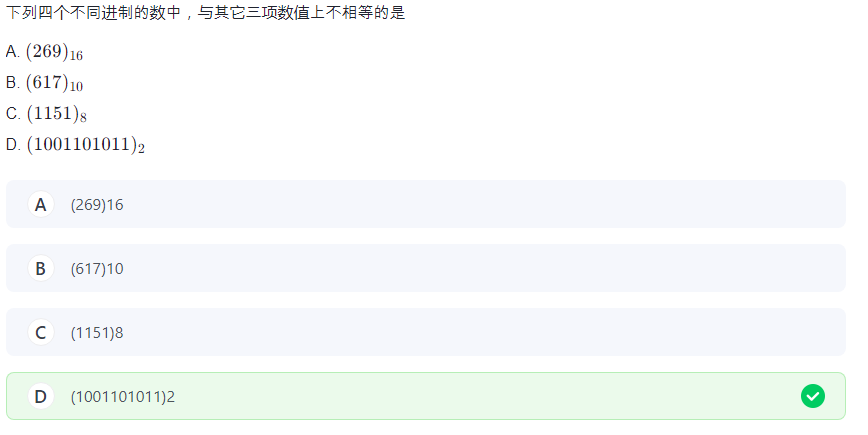 讲讲我的做法:
讲讲我的做法:
先不管 10 进制,把 16 进制的每一位转化成 2 进制,每一位占四个空。
8 进制同样,每一位占三个空,然后和二进制对比。
发现两个都不相等,那有问题的就是二进制。
5.阅读程序 2
#include <iostream>
using namespace std;int main()
{unsigned short x, y;cin >> x >> y;x = (x | x << 2) & 0x33;x = (x | x << 1) & 0x55;y = (y | y << 2) & 0x33;y = (y | y << 1) & 0x55;unsigned short z = x | y << 1;cout << z << endl;return 0;
}
当年在初赛场上看到这道题,蒙。
char 是字符类型,会改变答案。
229 这个答案到底是谁想出来的,像我这种 x 和 y 代反的智慧人真的会选。
6.组合数
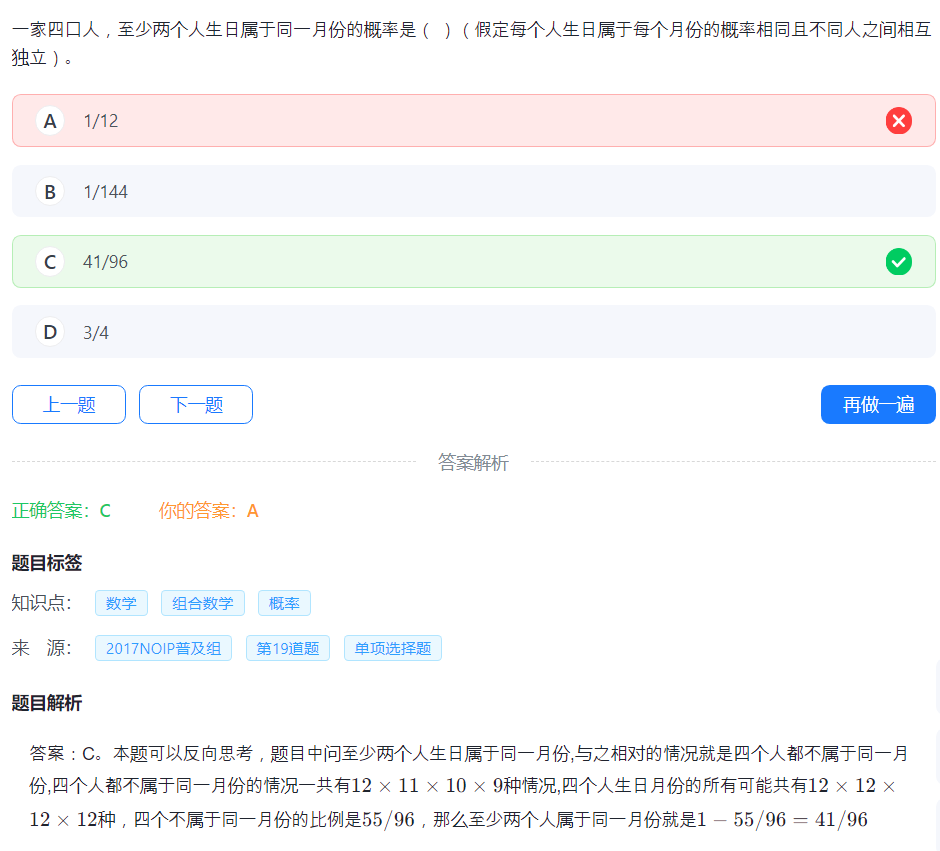
我好像错过很多次这道题,1/12 是特定两个人相同的概率。
7.组合数 2

首先计算不重复的,再确定第一位枚举重复的,我是智慧人。
8.组合数 3
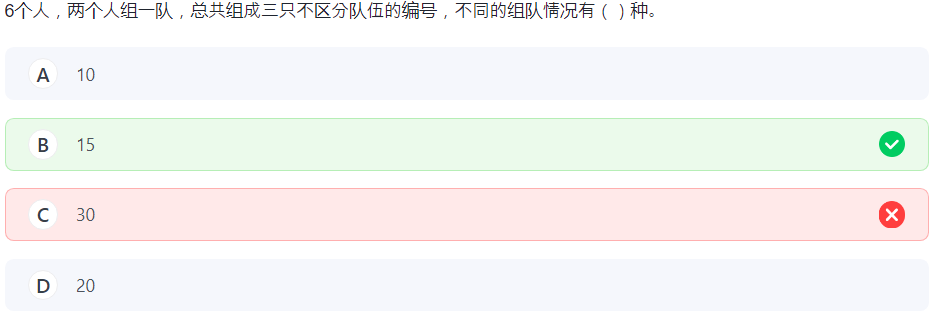
算乘法还能算错。
附:插板法
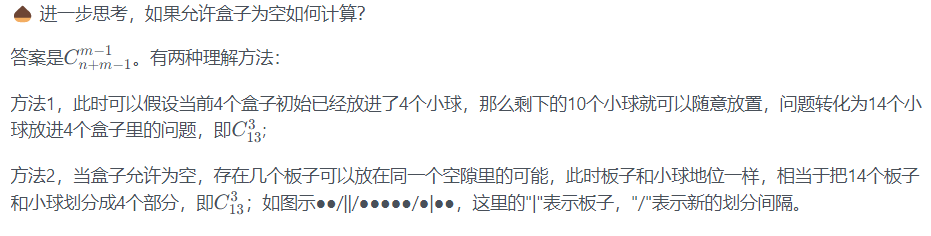
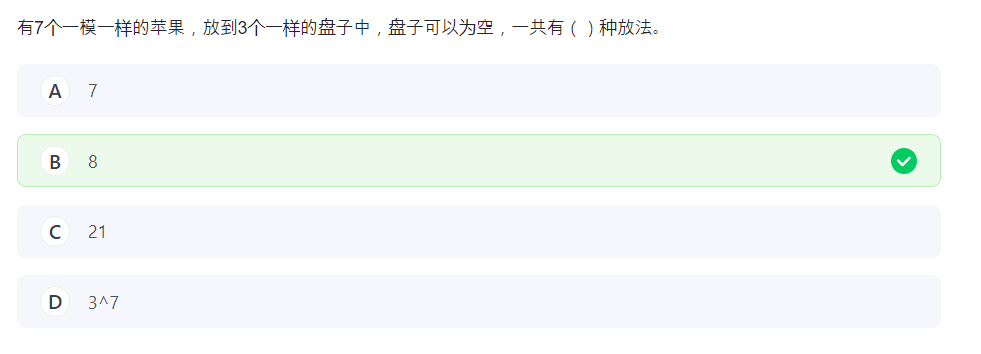
这种盒子一样的不能用插板法。只能老老实实枚举。
9.组合数 4
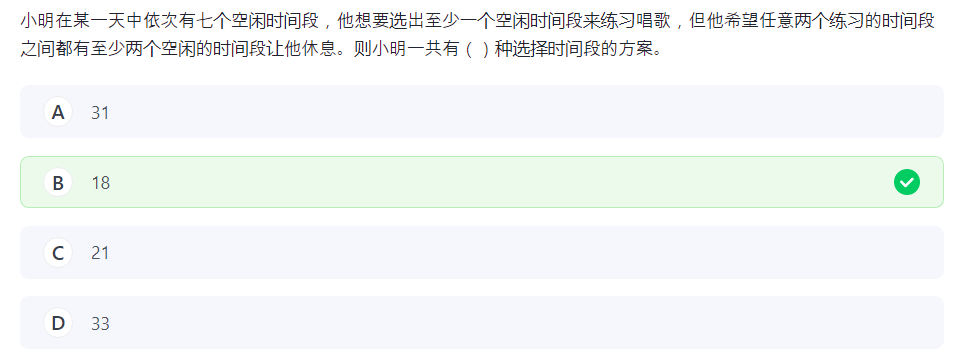
嘛还挺好玩的。
枚举选的练习段数,段数为 2 时把两段空段与后面的练习段绑定,方案为 ,因为要固定练习段的前后。
10.组合数 5

一开始算的是 12 * 21 * 20 / 2 = 2520,又想着如果先选的保险女生 A 和后选的女生 B,
两者在另一种情况中选反了,会导致答案多出来。
那还不如先一锅粥乱选,21 * 20 * 19 / (1 * 2 * 3)= 1530,
再减掉全是男生的方案 10 * 9 * 8 /(1 * 2 * 3)= 120,1530 - 120 = 1420。
感觉组合数最难的是区分特定和非特定,以及是否选重。
11.字节

KMGT
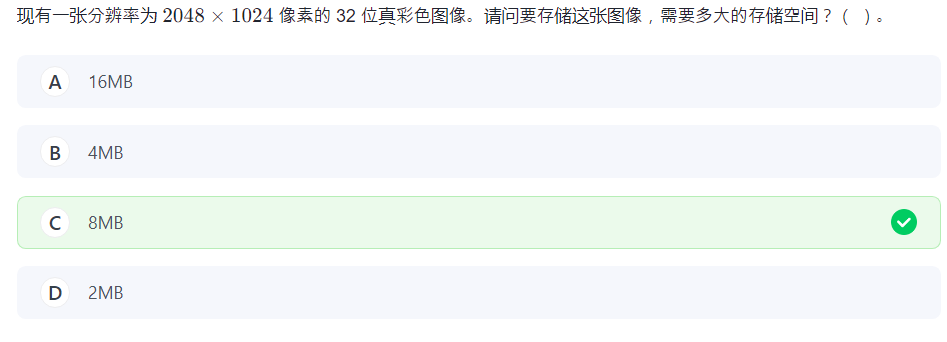
几位就是几个二进制位 bit,除以 8 就好。
12.地址总线
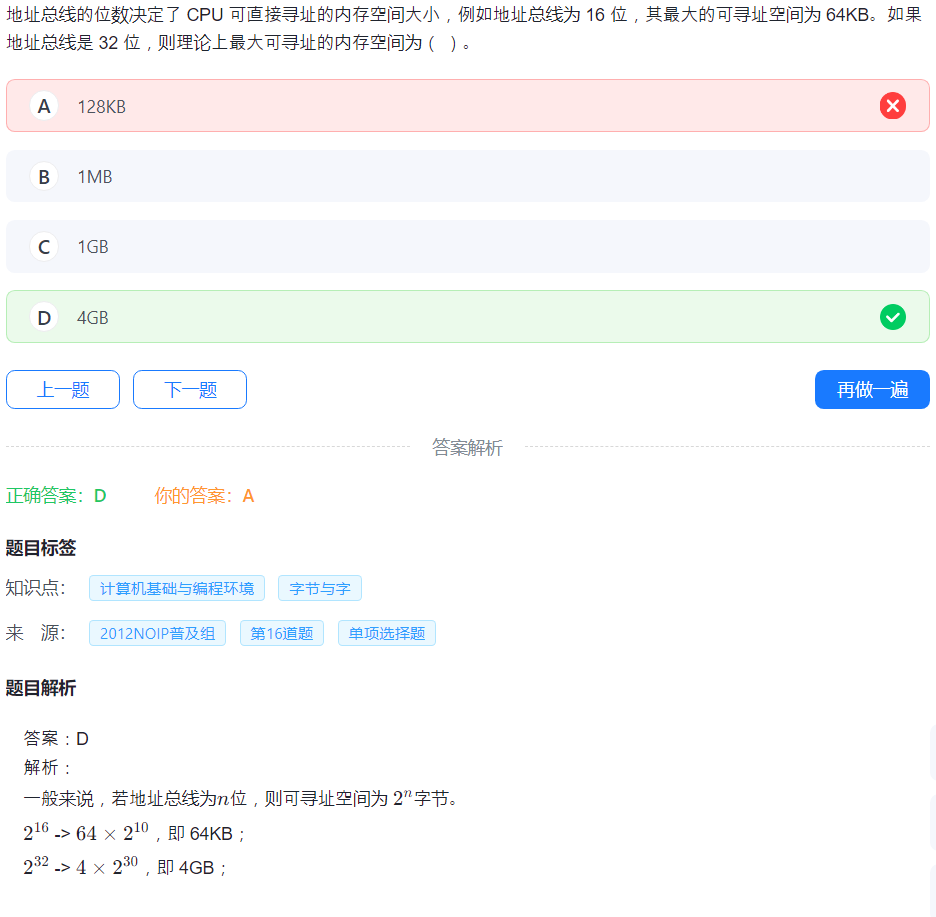
(这个是常识吗?!)
13.指针
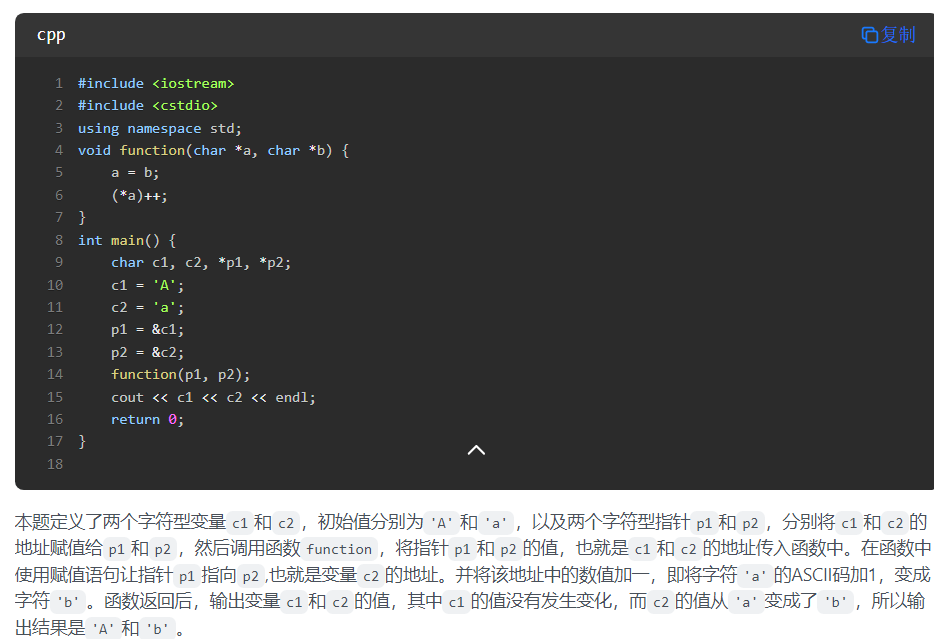
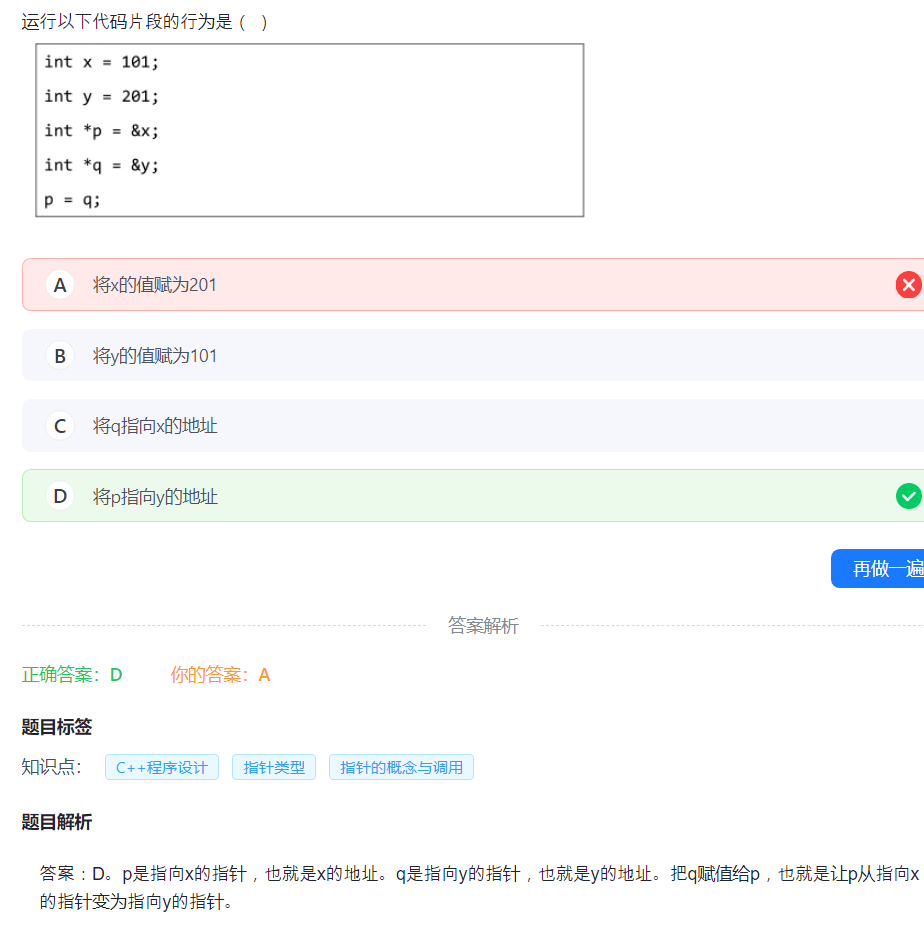
指针的等号是指向,不是赋值。
14.数据类型
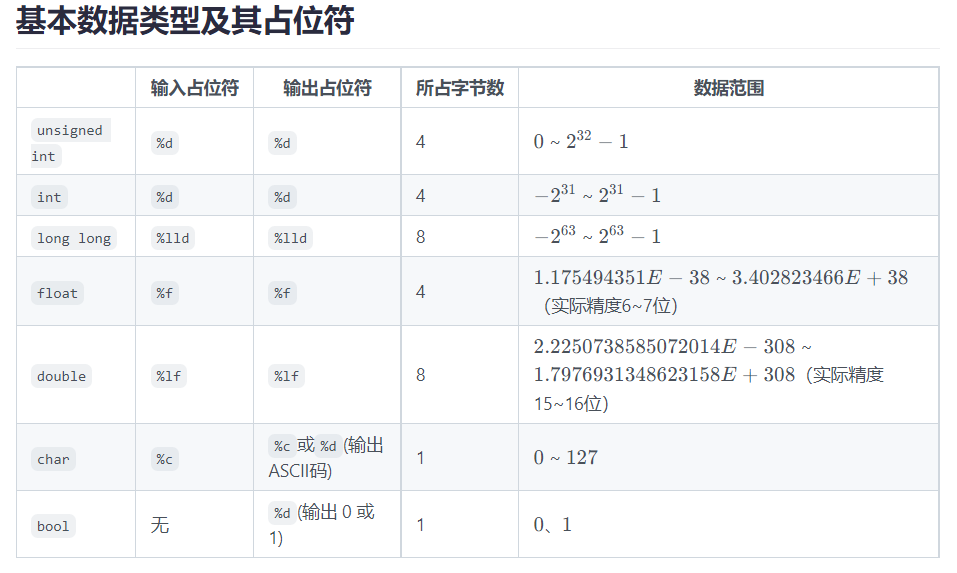
补充:
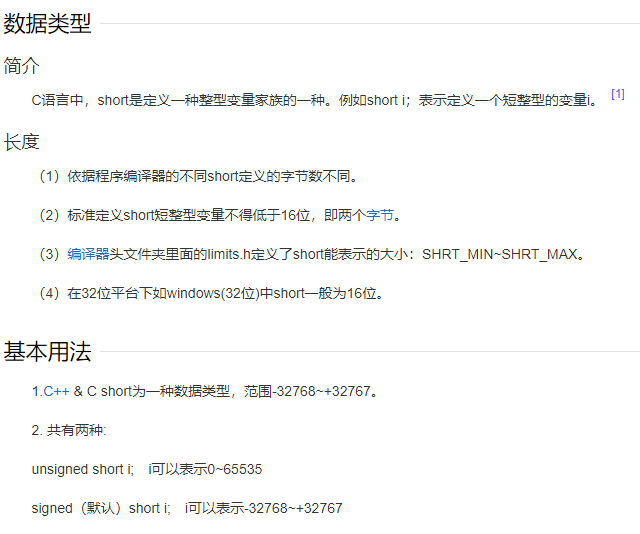
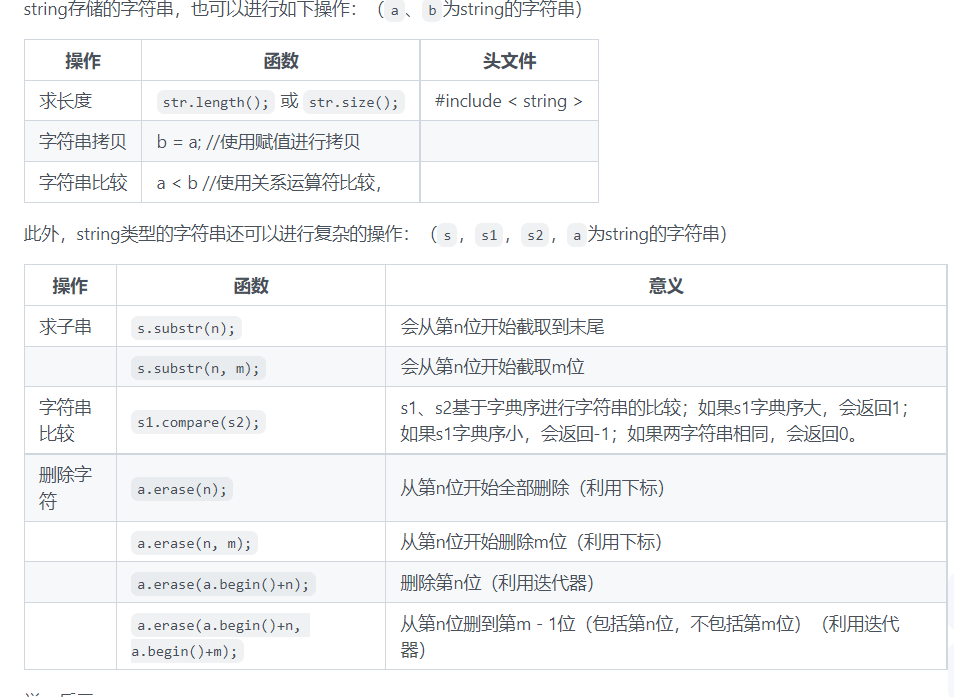
15.字符串
char str[100]; 可以存储最长为99个字符的字符串,因为最后的空字符 '\0' 也要存进来。

string:
16.阅读程序 3
#include <iostream>
using namespace std;int n, k;int solve1() {int l = 0, r = n;while (l <= r) {int mid = (l + r) / 2;if (mid * mid <= n) l = mid + 1;else r = mid - 1;}return l - 1;
}double solve2(double x) {if (x == 0) return x;for (int i = 0; i < k; i++)x = (x + n / x) / 2;return x;
}int main() {cin >> n >> k;double ans = solve2(solve1());cout << ans << ' ' << (ans * ans == n) << endl;return 0;
}
在数学中当趋近无限的时候,两者会相等返回 1,但浮点类型精度有限,两者不会相等。
(原来这就是传说中的牛顿迭代法!)
17.阅读程序 4
#include<iostream>
using namespace std;
int main()
{string ch;int a[200];int b[200];int n, i, t, res;cin >> ch;n = ch.length();for (i = 0; i < 200; i++)b[i] = 0;for (i = 1; i <= n; i++){a[i] = ch[i - 1] - '0';b[i] = b[i - 1] + a[i];}res = b[n];t = 0;for (i = n; i > 0; i--){if (a[i] == 0)t++;if (b[i - 1] + t < res)res = b[i - 1] + t;}cout << res << endl;return 0;
}输入:1001101011001101101011110001
输出:11
在 i = 3 或者 4 的时候,b[i - 1] + t 为 11。
(其实很简单,只要你不像我一样把最小看成最大)
18.链表

虽然 A 很离谱,但 C 确实是正确的。
(我想的是 STL 的 vector)
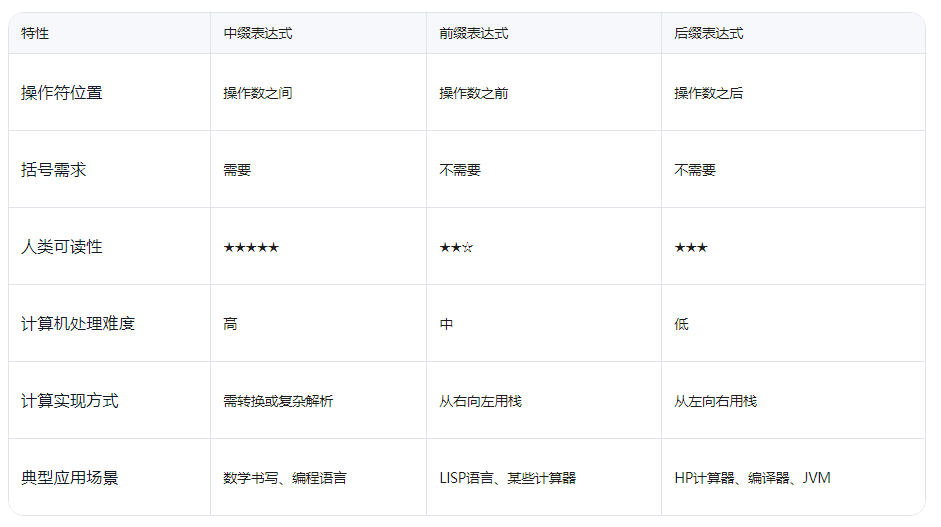
19.前中后缀表达式
20.队列快照

我的做法:
能分成的几组:
(1,1,6),(1,2,5),(1,3,4),(2,2,4),(2,3,3)
1(空集)+
6(单个数字)+
6(1 开头的两个数字组:11,12,13,14,15,16)+
5(2 开头的两个数字组:21,22,23,24,25)+
4(3 开头的两个数字组:31,32,33,34)+
3(4 开头的两个数字组:41,42,43)+
2(5 开头的两个数字组:51,52)+
1(6 开头的两个数字组:61)
= 21
(1,1,6),(1,2,5),(1,3,4),(2,2,4),(2,3,3)
排列:3 + 6 + 6 + 3 + 3 = 18
21 + 18 = 49
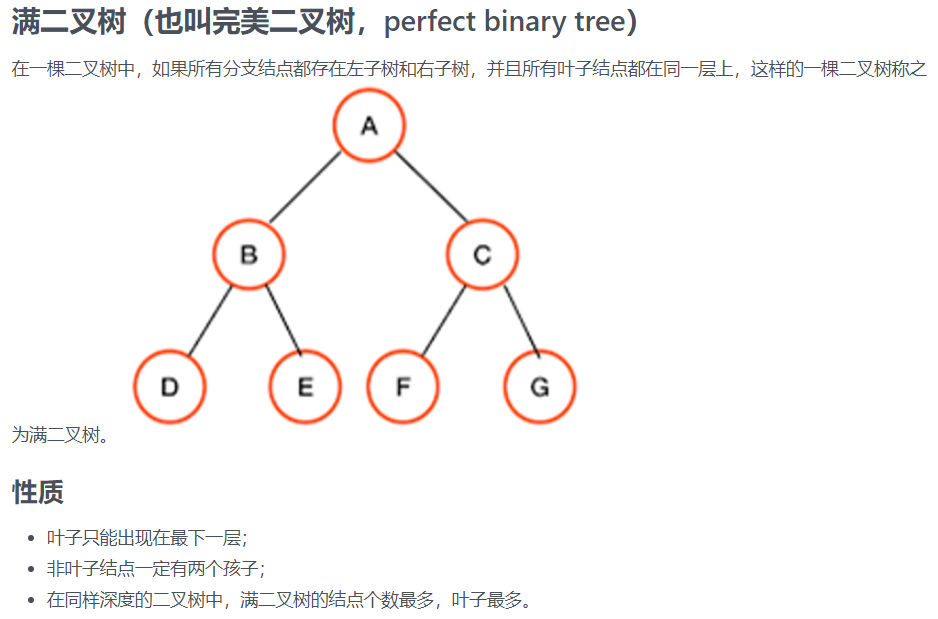
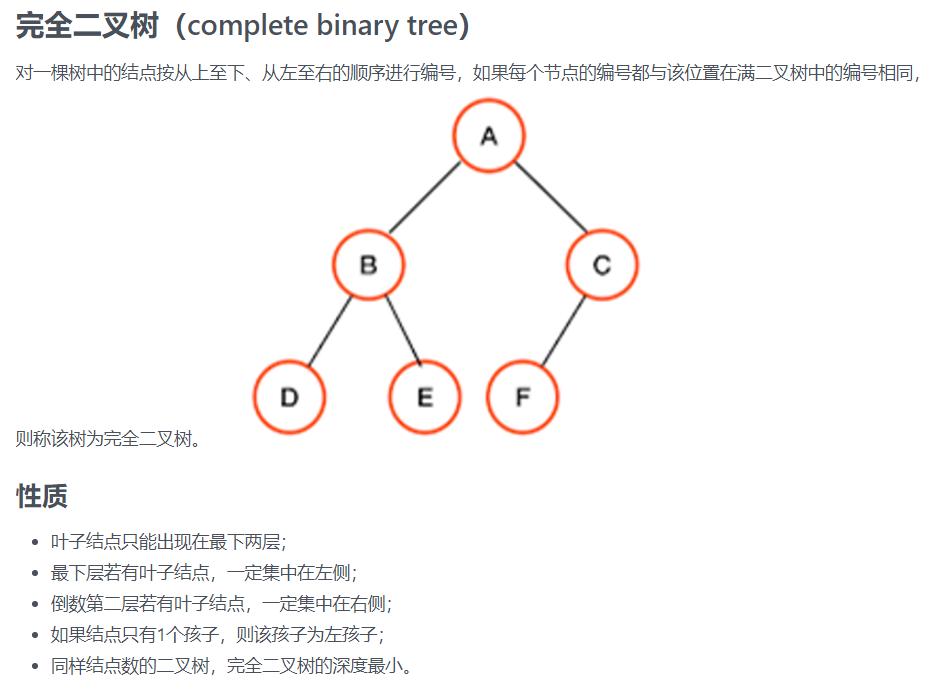
21.二叉树


![]()
我的做法:
先举个例子:
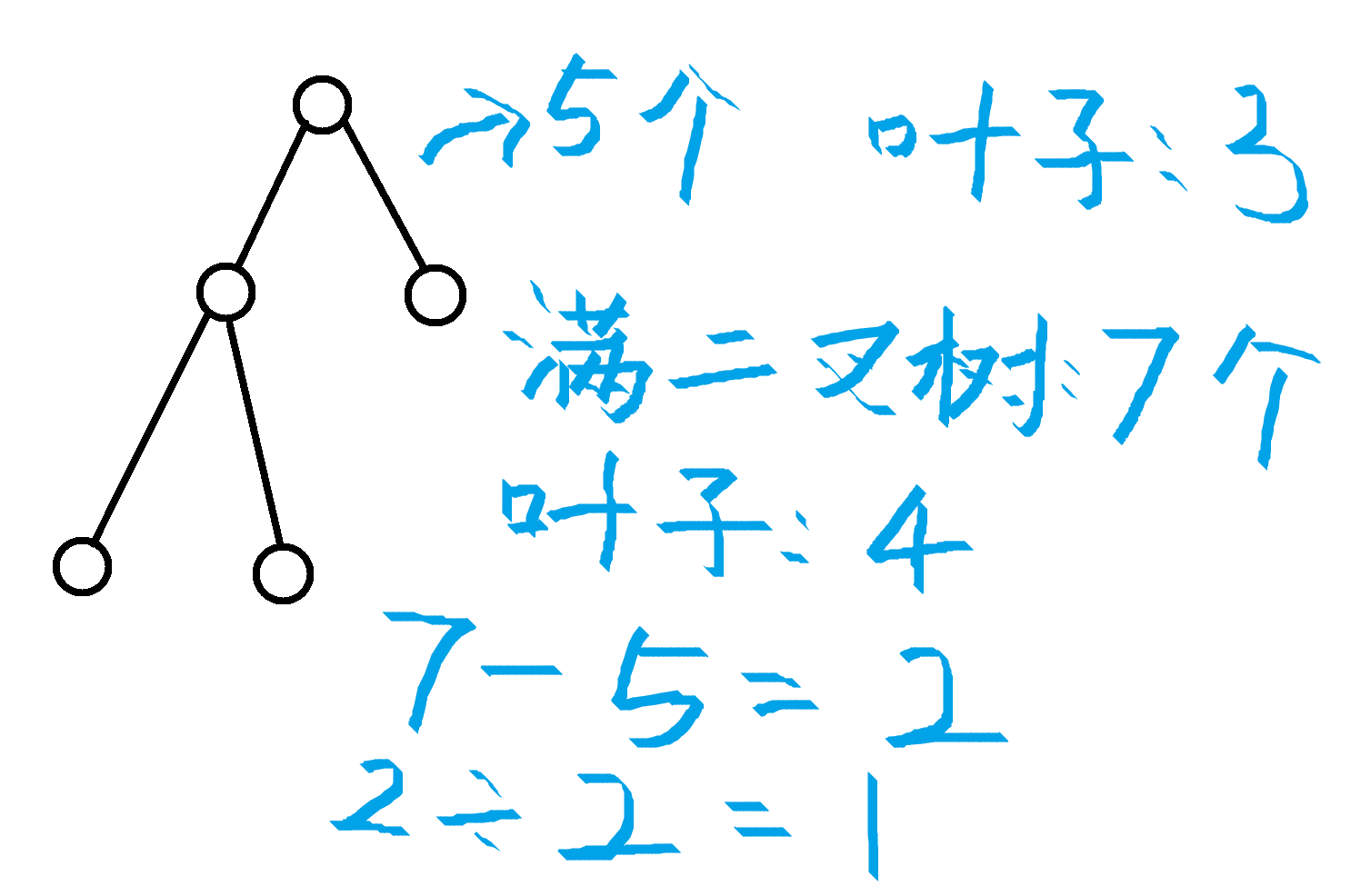
那么满二叉树的节点数为 2047,2047 - 2015 = 32,32 / 2 = 16,1024 - 16 = 1008
22.咬文嚼字
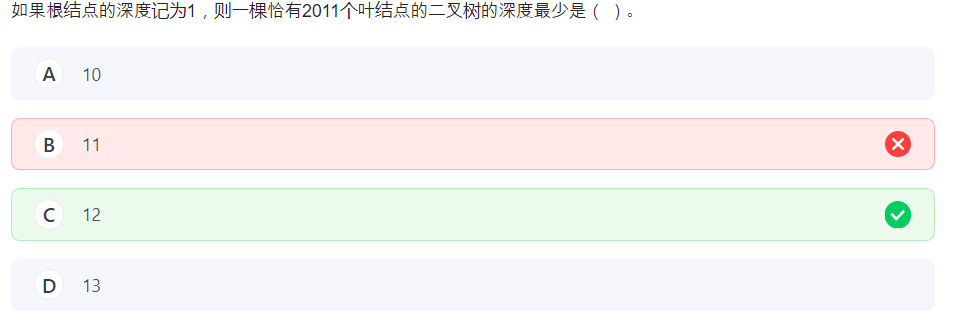
叶节点。
23.前中后序遍历

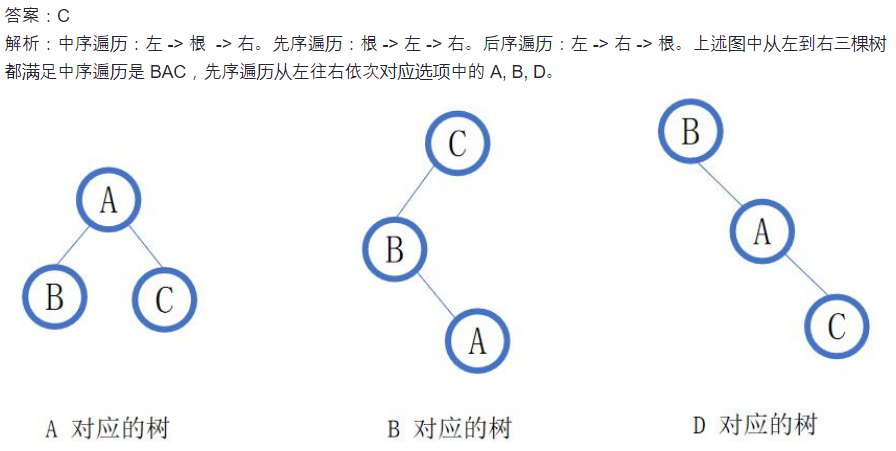
其实先序遍历 CAB 也可以。
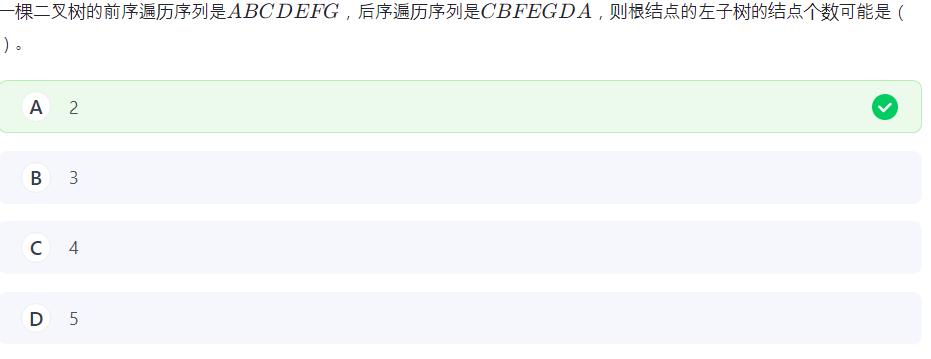
虽然但是我想画个图:
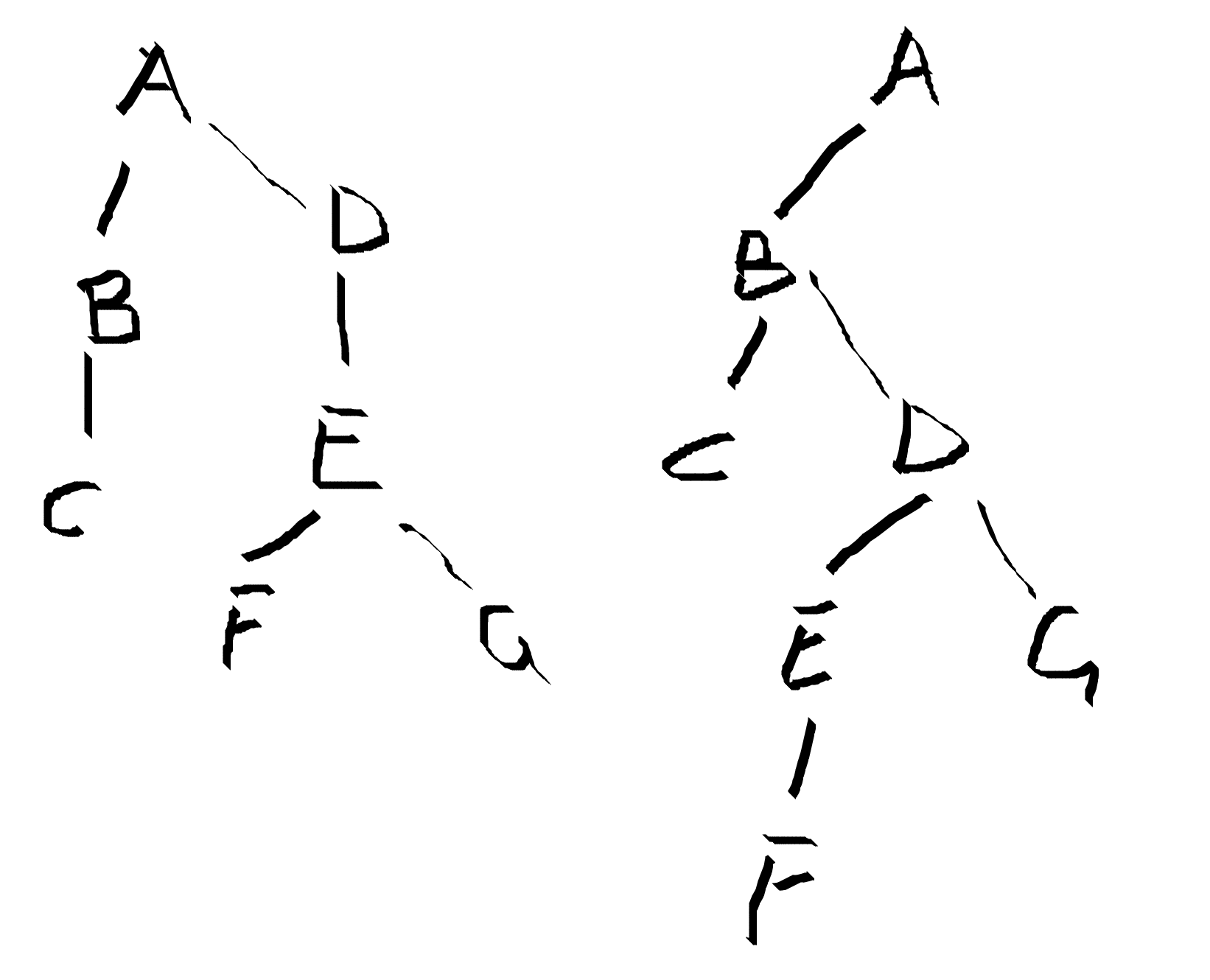
24.变种/三叉树
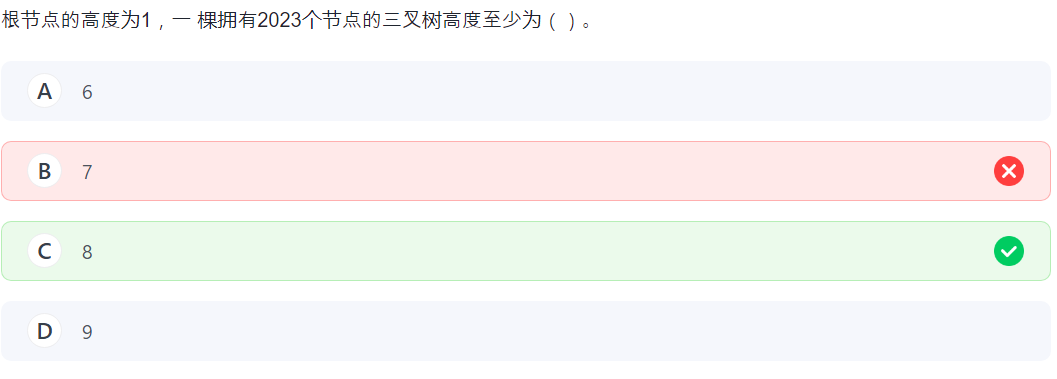
没招了一层层加:
1 + 3 + 9 + 27 + 81 + 243 + 729 = 1093,现在有 7 层还得多一层,8 层。
25.图论
很喜欢欧拉,所以截了。
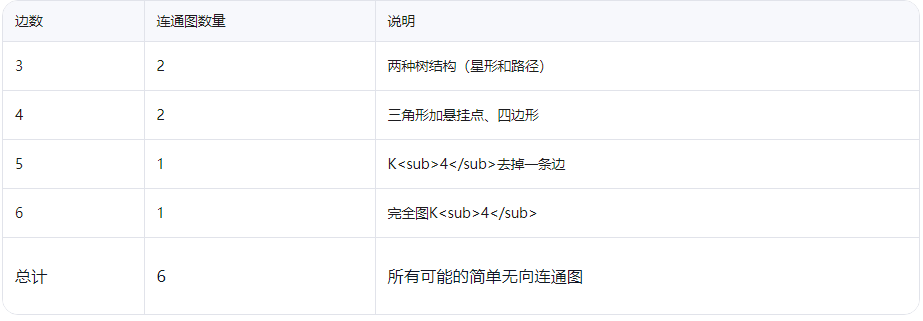
要注意的是点是完全一样的。
26.算法复杂度
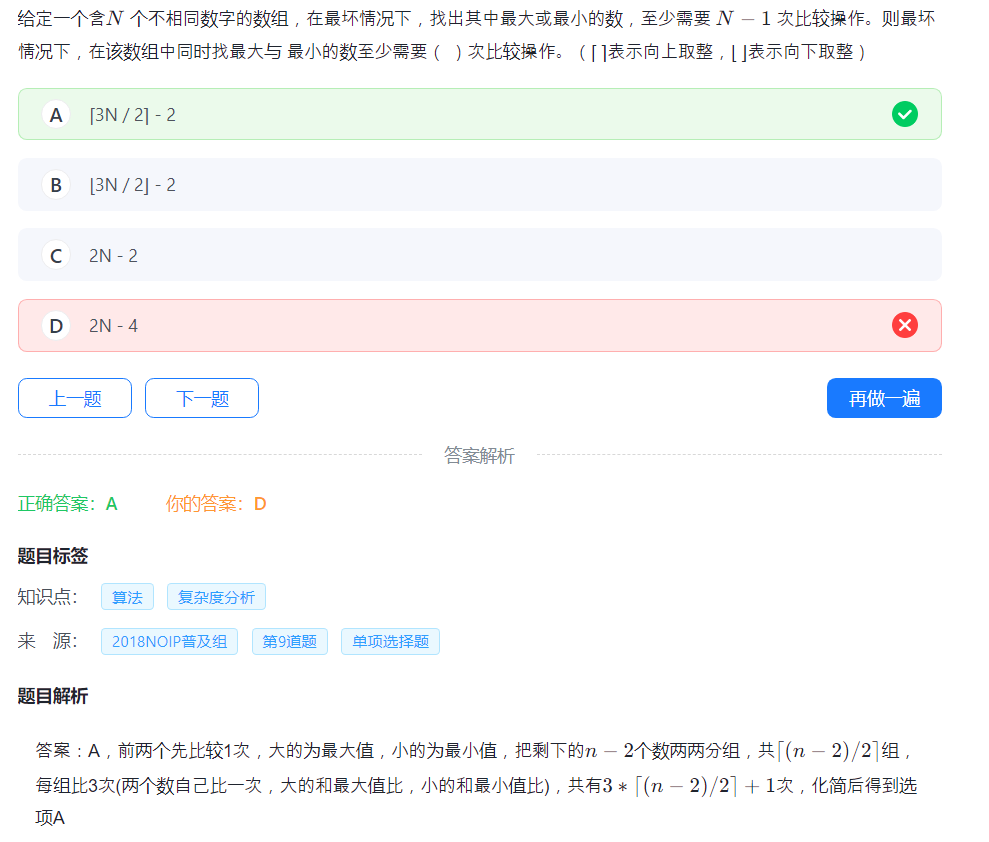
这道我至少错四五遍了。

(伪代码真难看)


没啥好说的,代入算就行,我是智慧人。
27.阅读程序 5

选 A,我是智慧人。
28.阅读程序 6
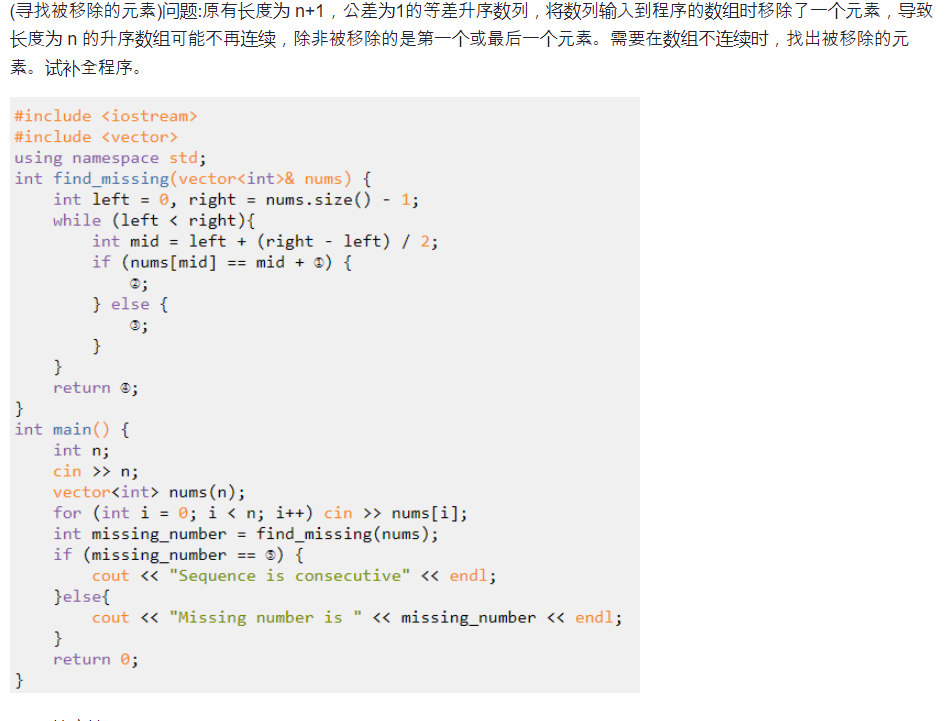
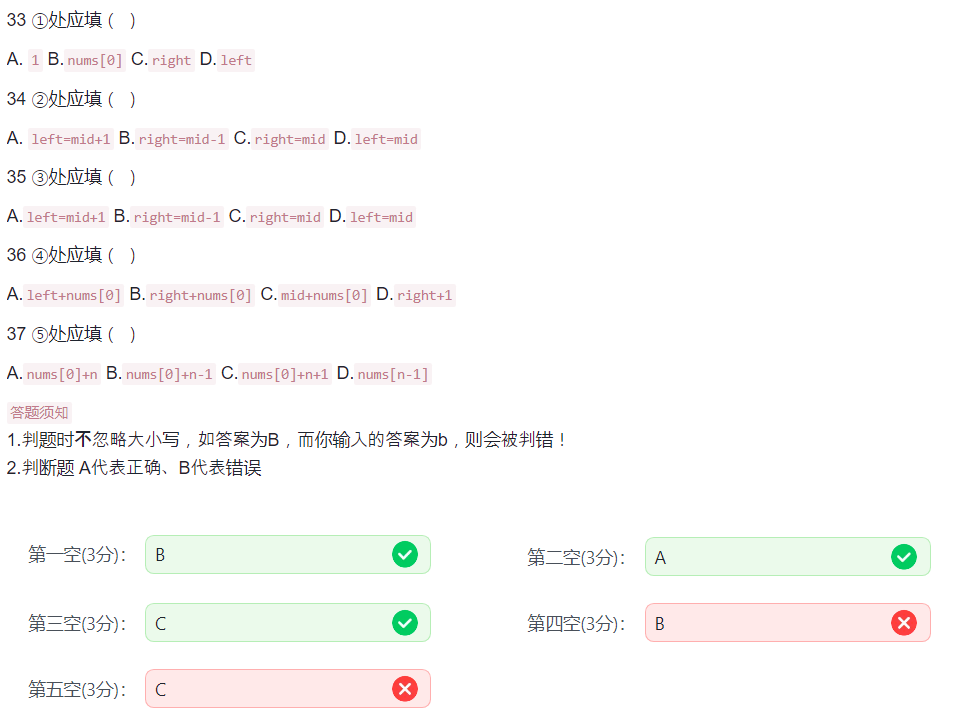
#include <stdio.h>struct point {int x, y, id;
};int equals(struct point a, struct point b) {return a.x == b.x && a.y == b.y;
}int cmp(struct point a, struct point b) {return ①;
}void sort(struct point A[], int n) {for (int i = 0; i < n; i++)for (int j = 1; j < n; j++)if (cmp(A[j], A[j - 1])) {struct point t = A[j];A[j] = A[j - 1];A[j - 1] = t;}
}int unique(struct point A[], int n) {int t = 0;for (int i = 0; i < n; i++)if (②)A[t++] = A[i];return t;
}int binary_search(struct point A[], int n, int x, int y) {struct point p;p.x = x;p.y = y;p.id = n;int a = 0, b = n - 1;while (a < b) {int mid = ③;if (④)a = mid + 1;else b = mid; }return equals(A[a], p);
}#define MAXN 1000
struct point A[MAXN];int main() {int n;scanf("%d", &n);for (int i = 0; i < n; i++) {scanf("%d %d", &A[i].x, &A[i].y);A[i].id = i;}sort(A, n);n = unique(A, n);int ans = 0;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)if (⑤ && binary_search(A, n, A[i].x, A[j].y) && binary_search(A, n, A[j].x, A[i].y)) {ans++;}printf("%d\n", ans); return 0;
}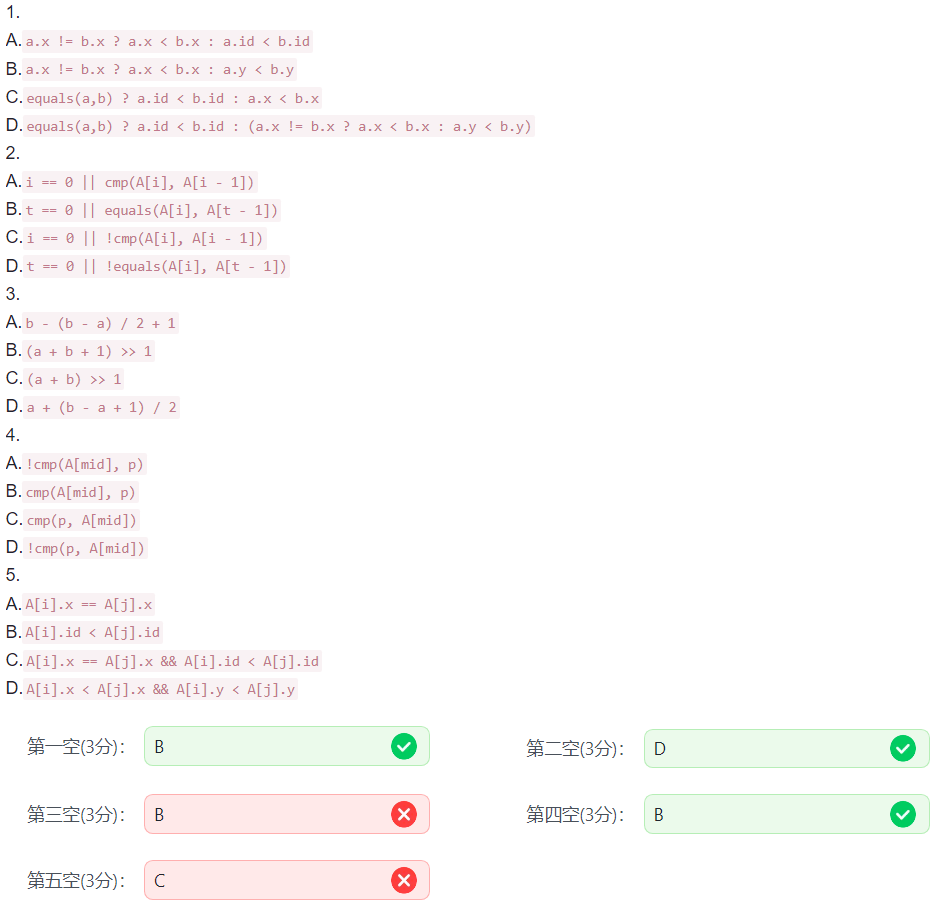
二分那个,带入 l = 0,r = 1,如果 mid = (l + r + 1) / 2 = 1,那么 l = mid + 1 就越界了。
最后那个纯属我闹谭。
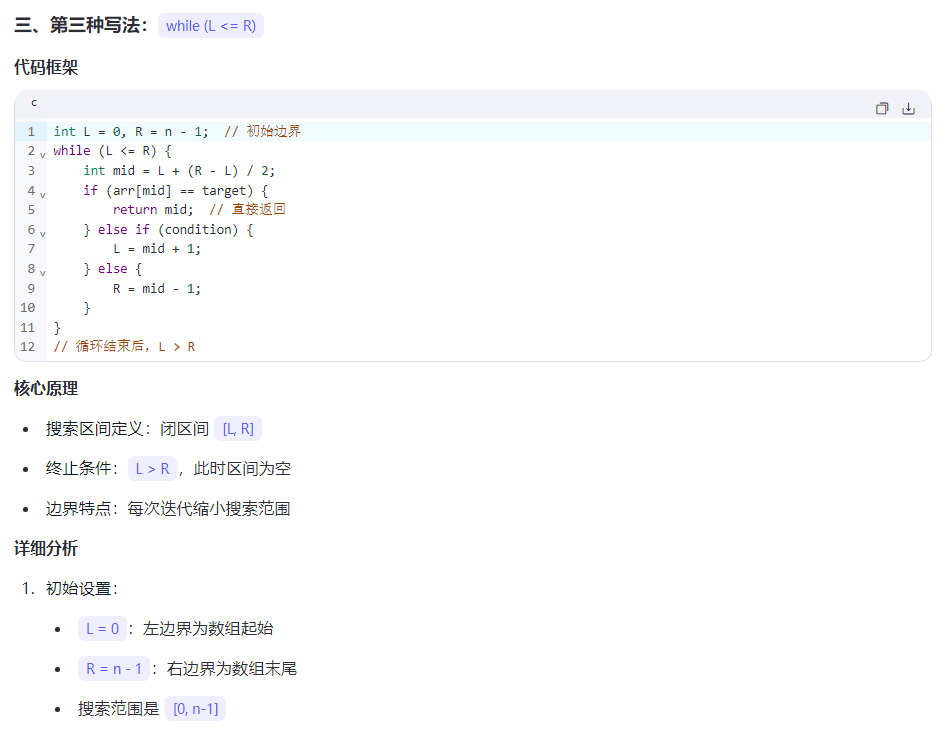
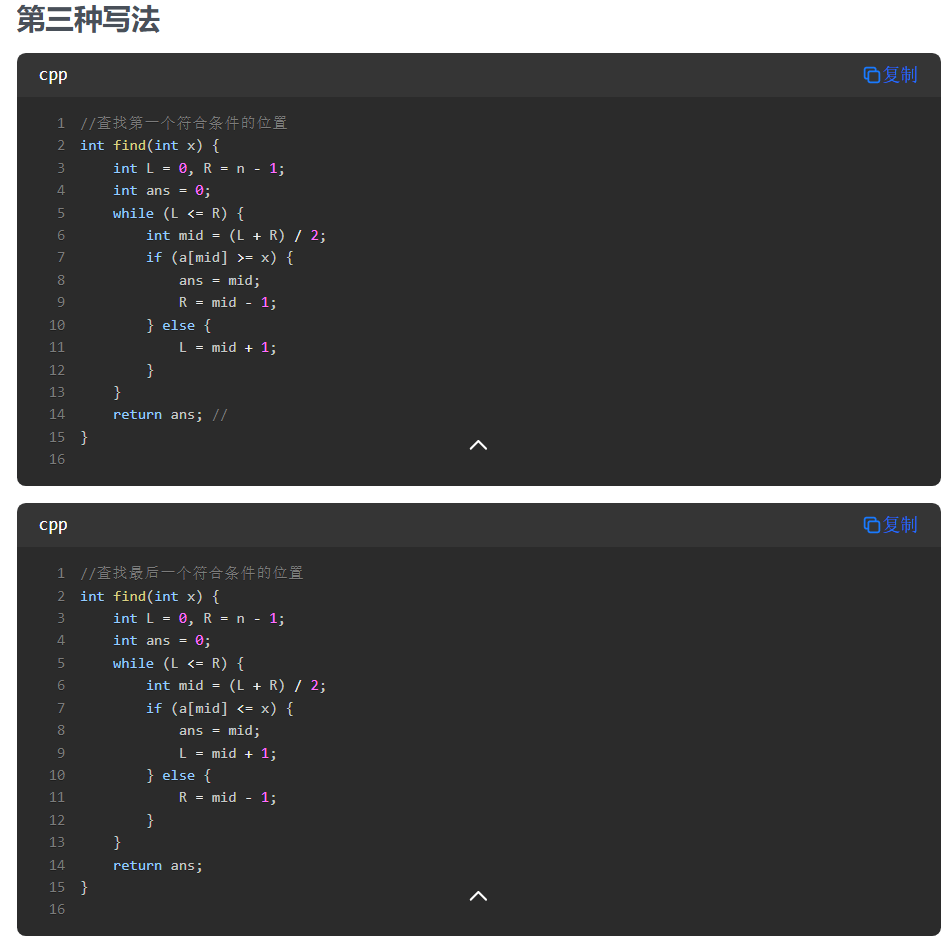
29.二分
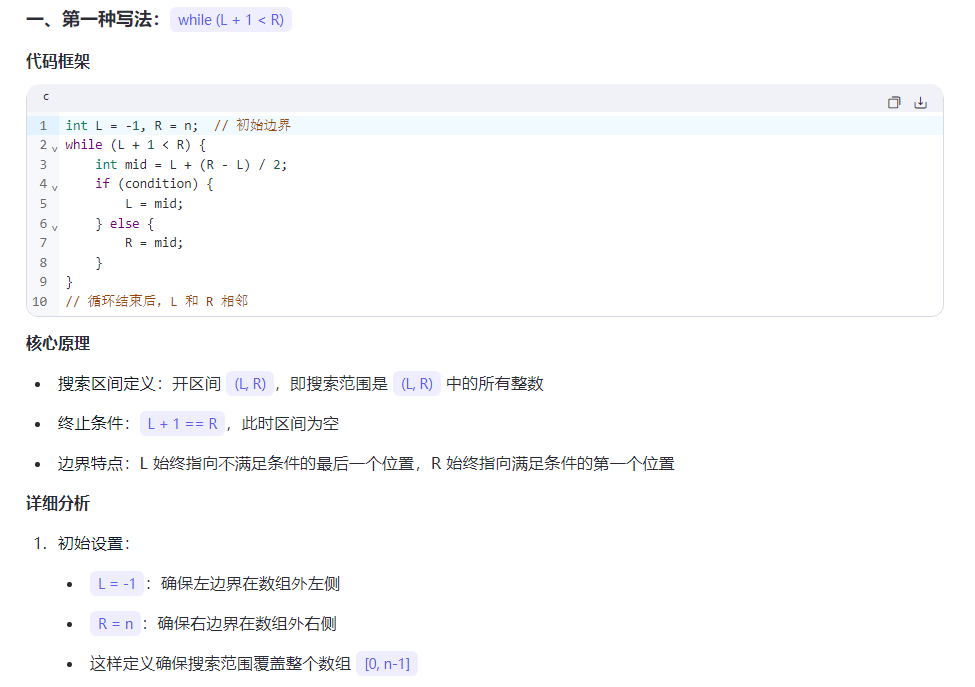
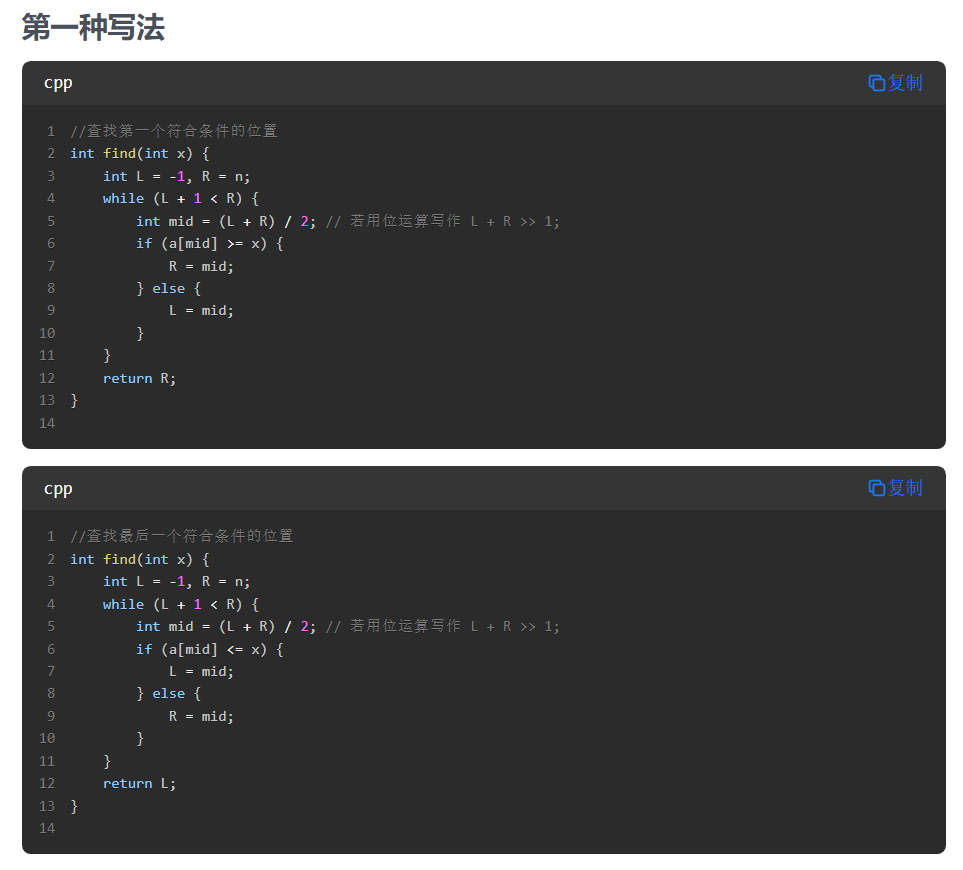
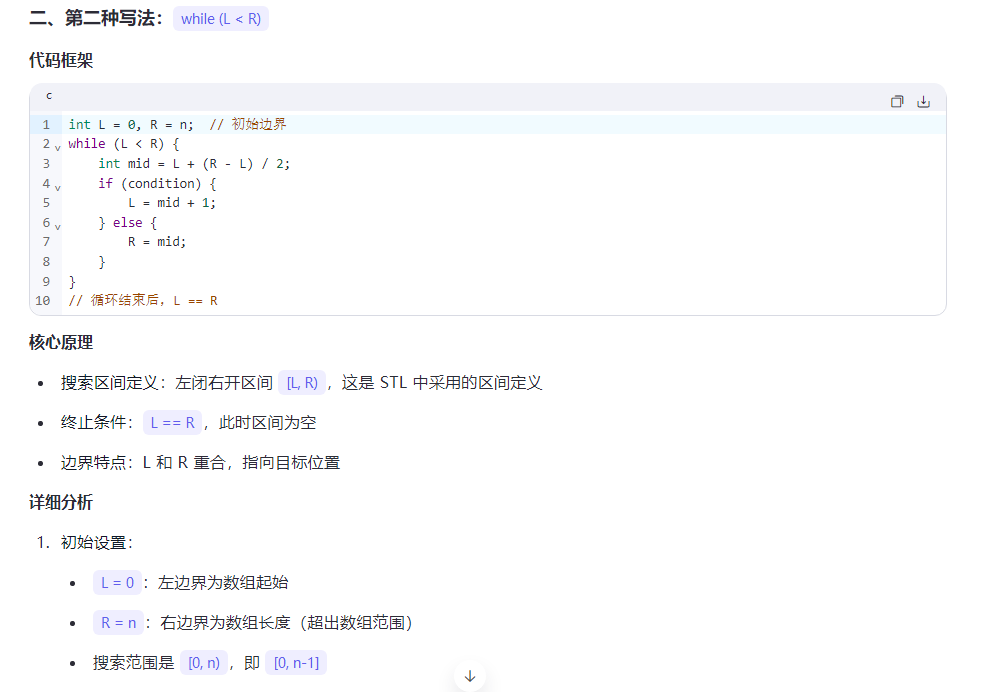
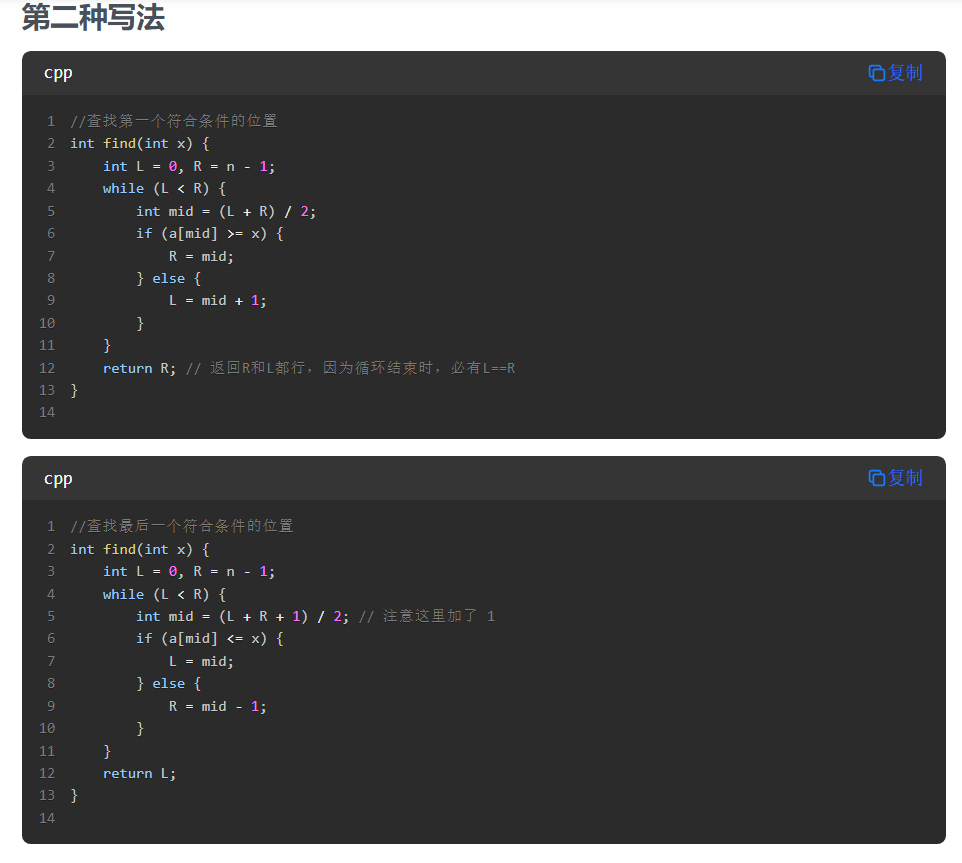

第二种写法的最后一个代码,维护的关键不变量:
R始终指向一个可能的解或解的右侧L会不断向右移动,直到达到最后一个满足条件的位置
在每次迭代中:
- 如果
a[mid] <= x,说明mid位置满足条件,且可能有更右边的元素也满足条件,所以L = mid - 如果
a[mid] > x,说明mid位置不满足条件,最后一个满足条件的位置一定在mid左边,所以R = mid - 1
30.阅读程序 7
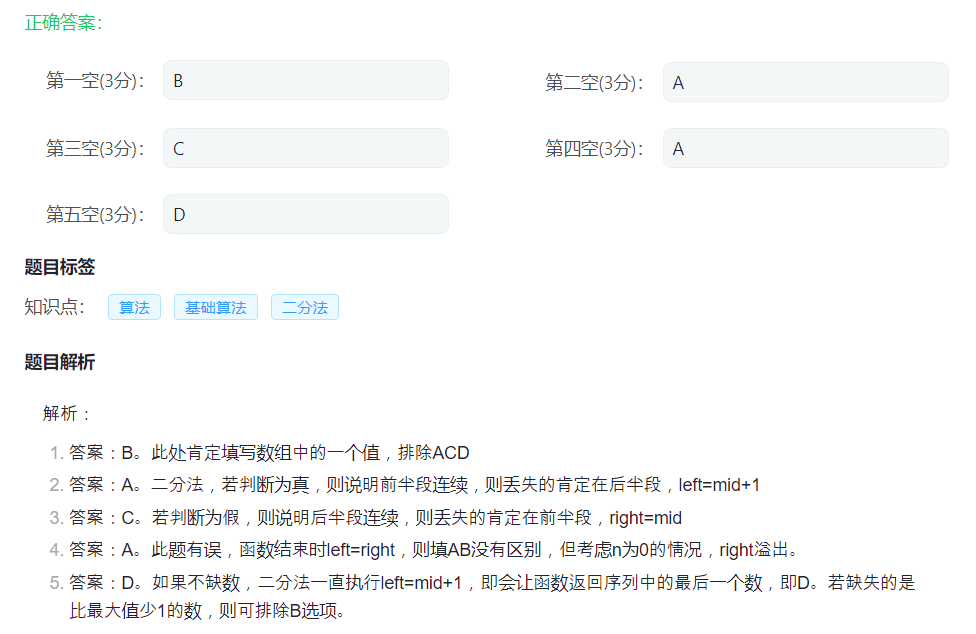
唉我好蠢,这个东西感觉比别的都难。
31.难*阅读程序 8
#include <stdio.h>
#include <string.h>char base[64];
char table[256];
char str[256];
char ans[256];void init()
{for (int i = 0; i < 26; i++) base[i] = 'A' + i;for (int i = 0; i < 26; i++) base[26 + i] = 'a' + i;for (int i = 0; i < 10; i++) base[52 + i] = '0' + i;base[62] = '+', base[63] = '/';for (int i = 0; i < 256; i++) table[i] = 0xff;for (int i = 0; i < 64; i++) table[base[i]] = i;table['='] = 0;
}void decode(char *str)
{char *ret = ans;int i, len = strlen(str);for (i = 0; i < len; i += 4) {(*ret++) = table[str[i]] << 2 | table[str[i + 1]] >> 4;if (str[i + 2] != '=')(*ret++) = (table[str[i + 1]] & 0x0f) << 4 | table[str[i + 2]] >> 2;if (str[i + 3] != '=')(*ret++) = table[str[i + 2]] << 6 | table[str[i + 3]];}
}int main()
{init();printf("%d\n", (int)table[0]);scanf("%s", str);decode(str);printf("%s\n", ans);return 0;
}
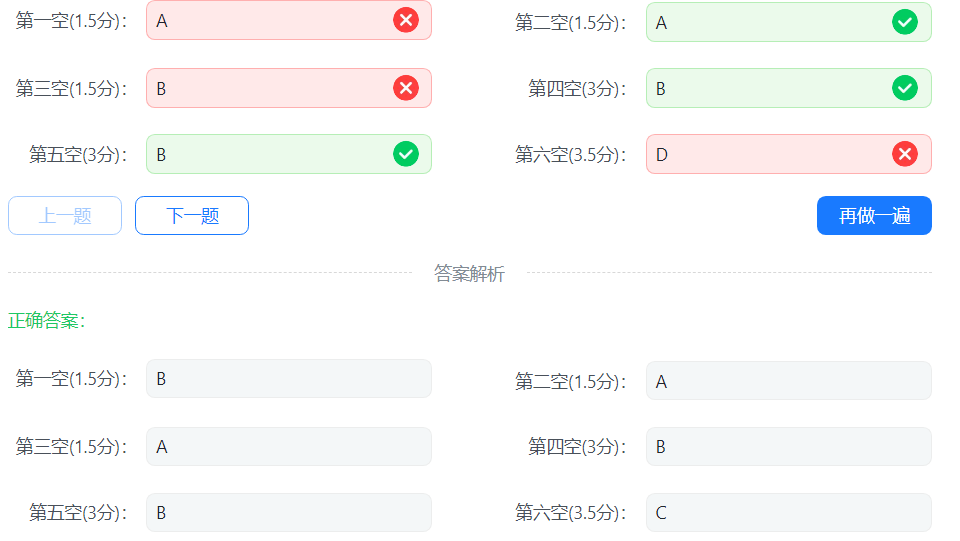


我忏悔,打表打的精疲力尽,一代入数据发现有俩错,一点不想写了乱蒙。
'A' = 65 'a' = 97 '空格' = 32 '0' = 48
32.网络

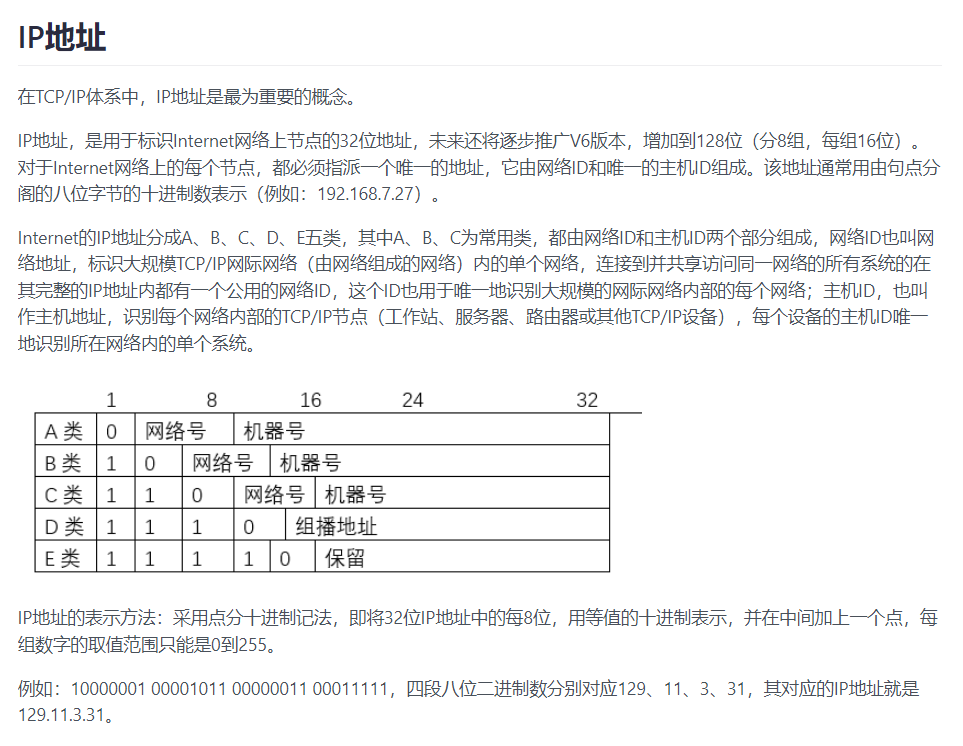
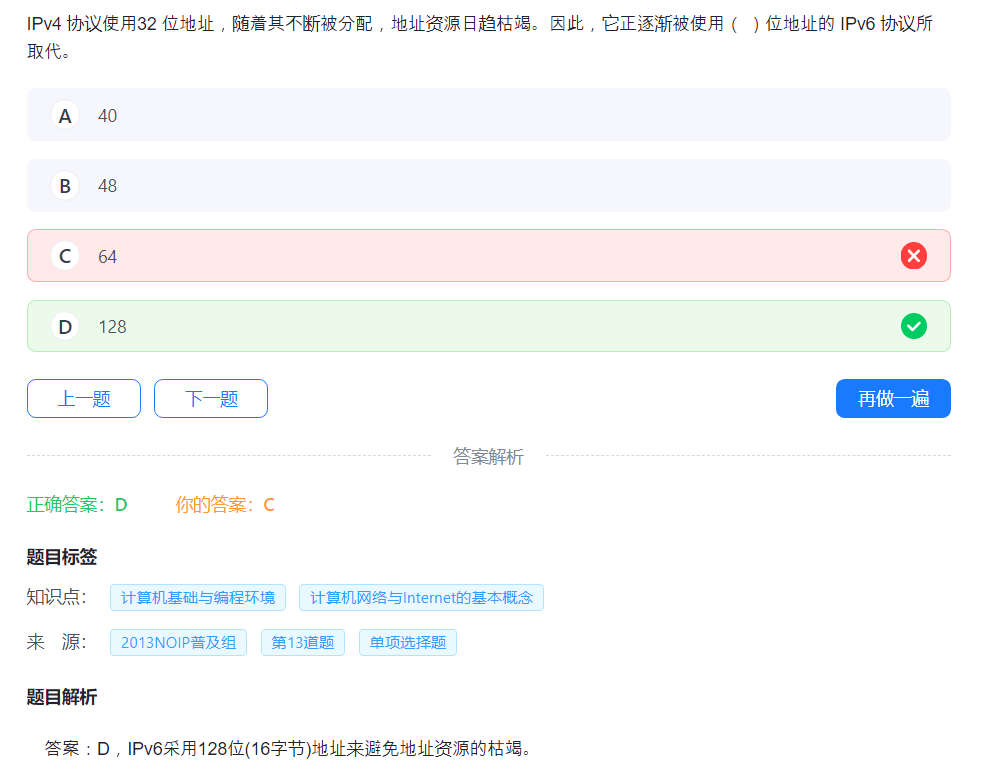


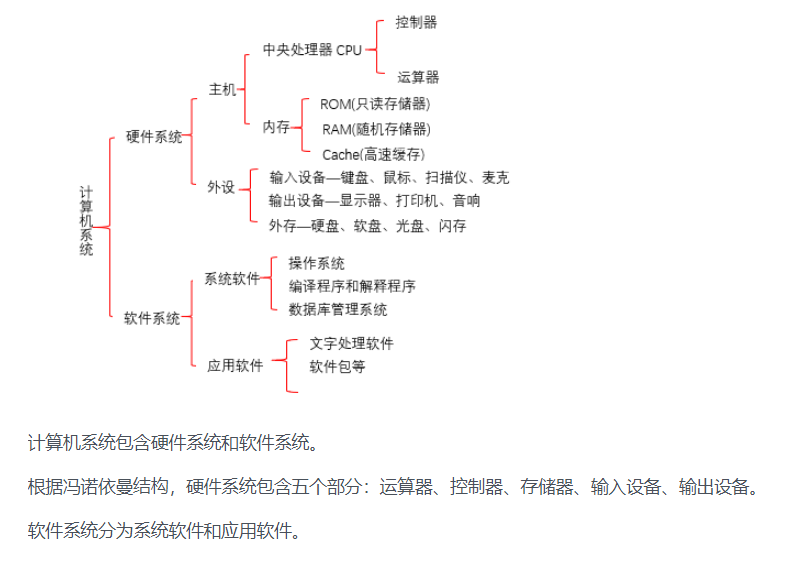
33.计算机





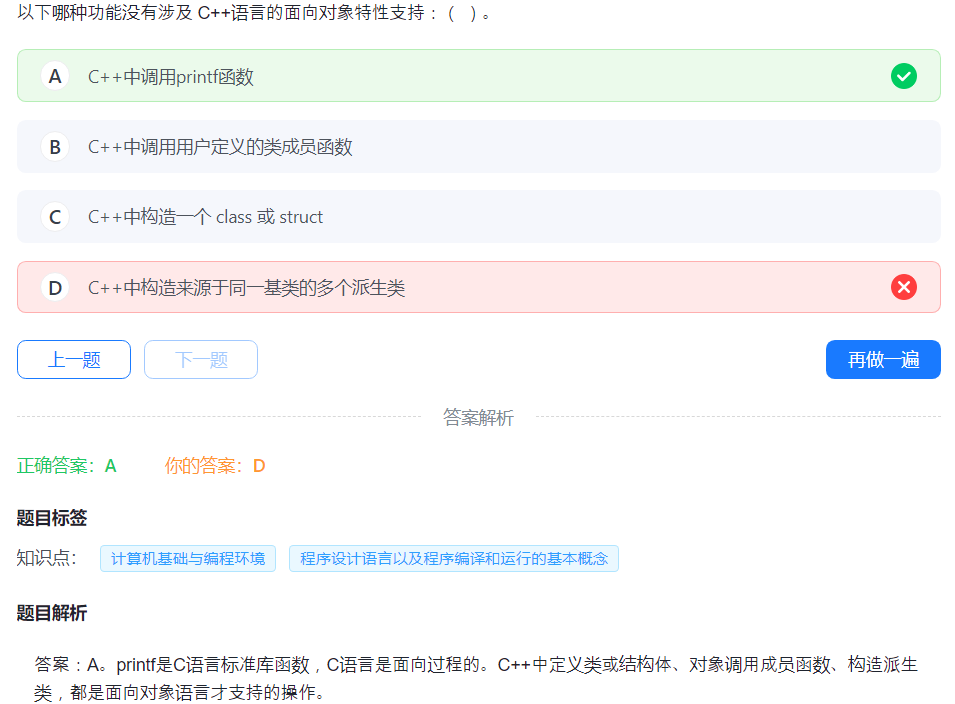
面向对象编程语言特性:
封装(Encapsulation):将数据和操作封装在一起,隐藏内部实现
继承(Inheritance):允许新类基于现有类创建,复用代码
多态(Polymorphism):同一接口表现出多种形态
抽象(Abstraction):提取共性,隐藏复杂性
-
抽象:我们决定要做一个"汉堡",关注的是它应该有面包、肉饼和蔬菜,而不关心具体用什么肉、什么蔬菜(提取共性)
-
封装:每个组件(面包、肉饼、蔬菜)都准备好并保持自己的特性,厨师不需要知道面包是如何烤制的,只需要知道如何使用它(隐藏实现)
-
继承:我们可以基于基础汉堡创建"芝士汉堡"(加一片芝士)或"双层汉堡"(加一块肉饼),而不必从头开始制作(代码复用)
-
多态:当顾客说"我要一个汉堡"时,可以根据他们的选择提供不同类型的汉堡,但处理订单的流程是一样的(同一接口,多种实现)
B、C 和 D 分别对应着继承、封装和多态。
