OD C卷 - 计算三叉搜索树的高度

计算三叉搜索树的高度

• 定义构造三叉搜索树的规则如下：
  • 每个节点都存有一个数，当插入一个新的数时，从根节点向下寻找，直到找到一个空节点插入；
  • 如果数小于节点的数减去500，则将数插入节点的左子树；
  • 如果数大于节点的数据加500，则将数插入节点的右子树；
  • 否则将数插入节点的中子树
• 给一系列数，构造一棵三叉搜索树，并输出树的高度

输入描述：
第一行输入n，表示有n个数，范围【1， 10000】
第二行输入n个数
输出描述：
输出树的高度（根节点的高度为1）

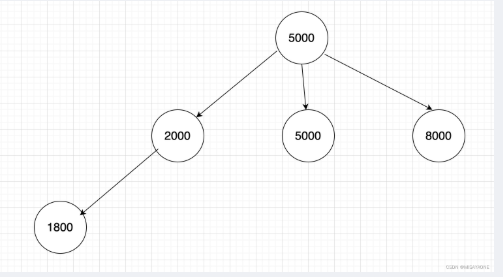
示例1
输入：
5
5000 2000 5000 8000 1800
输出：
3

 
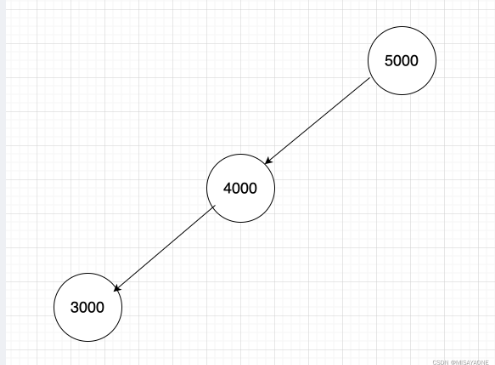
示例2
输入：
3
5000 4000 3000
输出：
3

思路：

• 类似构建二叉排序树（初始化空树，遍历数组）
• 递归统计树的高度；

n = int(input().strip())
arr = list(map(int, input().strip().split()))class Node:def __init__(self, data, left=None, mid=None, right=None):self.data = dataself.left = leftself.mid = midself.right = rightdef create_tree(root, e):if root is None:return Node(e)if e < root.data - 500:root.left = create_tree(root.left, e)elif e > root.data + 500:root.right = create_tree(root.right, e)else:root.mid = create_tree(root.mid, e)return rootdef count_height(root, h):if root is None:return hh += 1global heightheight = max(height, h)count_height(root.left, h)count_height(root.mid, h)count_height(root.right, h)root = None
for e in arr:root = create_tree(root, e)height = 0
count_height(root, 0)
print(height)