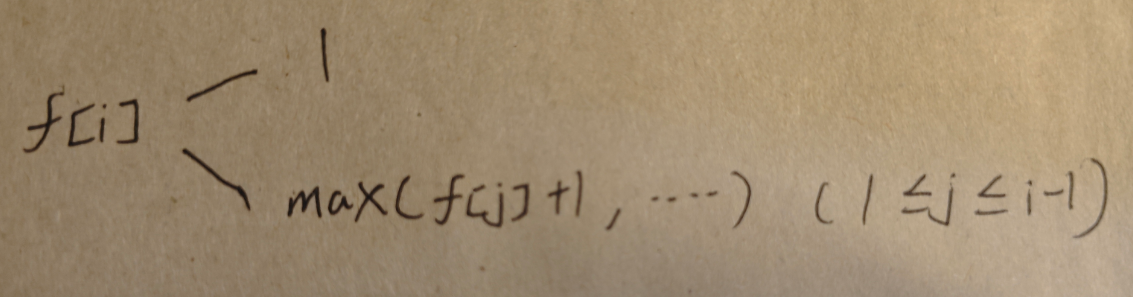算法题（207）：最长上升子序列（经典线性dp题）

审题：

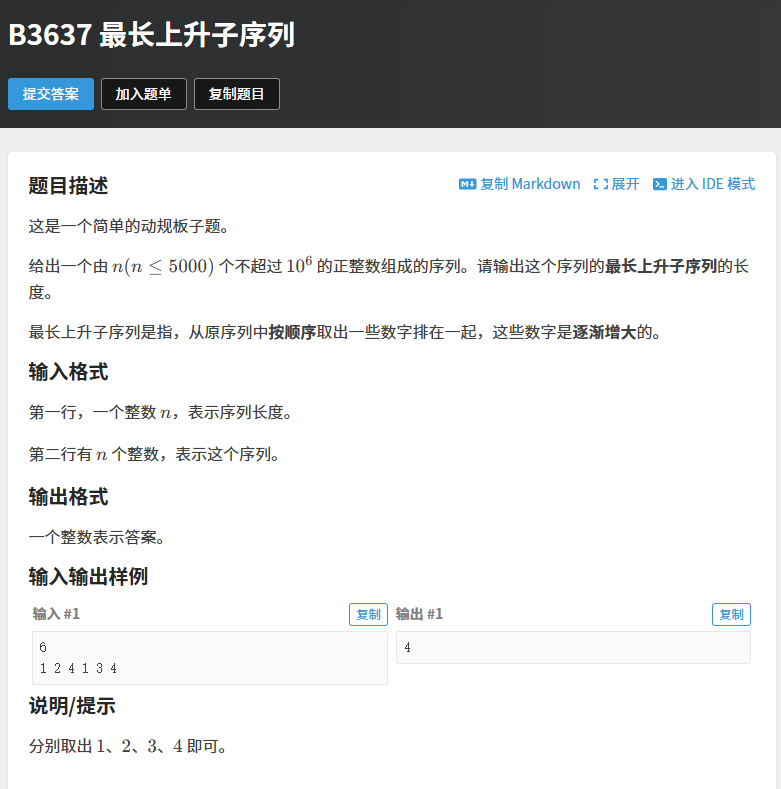
本题需要我们找到最长的上升子序列，然后输出最长的序列长度

思路：
方法一：动态规划

（1）状态表示：f[i]表示以第i个元素为结尾的上升子序列的最大长度

（2）状态转移方程：

上升子序列有两大状态，其一是只有i位置元素本身，序列长度就为1

其二是不仅包含i位置本身，且还有前面若干个元素

那么对于第二种情况，a[i]前面可以与其组成升序子序列的有效元素a[j]，一定满足a[j]<a[i]

(1 <= j <= i-1)

我们遍历所有满足该条件的元素的f[j]，然后维护出最大的f[j],那么此时最长序列长度就是maxf[j] + 1

（3）初始化：

由于我们在进行访问的时候不会出现越界访问的情况，所以不存在数组原始数据干扰，全部初始化为0即可

（4）填表顺序：从左到右

由于f[i]是依赖于f[j]求的，且j位于i左侧，所以我们需要先填写左侧的f

（5）答案输出：

题目要的是所有升序序列中的最大长度，所以我们遍历整个f数组，然后将f数组的最大值输出即可

解题：
 

#include<iostream>
using namespace std;
const int N = 5010;
int a[N], f[N];
int n;
int main()
{//数据录入cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}//填表for (int i = 1; i <= n; i++){int max_size = 1;for (int j = 1; j <= i - 1; j++){if(a[j] < a[i]) max_size = max(max_size, f[j] + 1);}f[i] = max_size;}//答案输出int ret = 0;for (int i = 1; i <= n; i++){ret = max(ret, f[i]);}cout << ret << endl;return 0;
}

注意：

1.初始化max_size为1,是因为无论哪种情况，长度一定大于等于1

B3637 最长上升子序列 - 洛谷