当前位置：首页 > news >正文

FlashAttention（V2）深度解析：从原理到工程实现

news 2025/9/15 5:35:34

FlashAttention（V2）深度解析：从原理到工程实现

引言

随着大模型参数规模的不断扩大和序列长度的增长，注意力机制的计算复杂度成为训练和推理的主要瓶颈。Flash Attention通过巧妙的内存管理和计算重排，在不改变数学语义的前提下大幅提升了注意力计算的效率。在Flash Attention V1的基础上，V2版本通过调整循环结构和优化并行策略，进一步提升了性能。

一、Flash Attention V1回顾

1.1 V1的核心思想

Flash Attention V1的核心在于分块计算和在线softmax算法。传统的注意力机制需要计算完整的注意力矩阵：

$Attention(Q,K,V) = softmax(QK^T/√d)V$

其时间复杂度为O(N²d)，空间复杂度也为O(N²)，其中N为序列长度，d为维度。对于长序列，这种二次复杂度会导致内存不足。

1.2 V1的分块策略

V1采用的策略是：

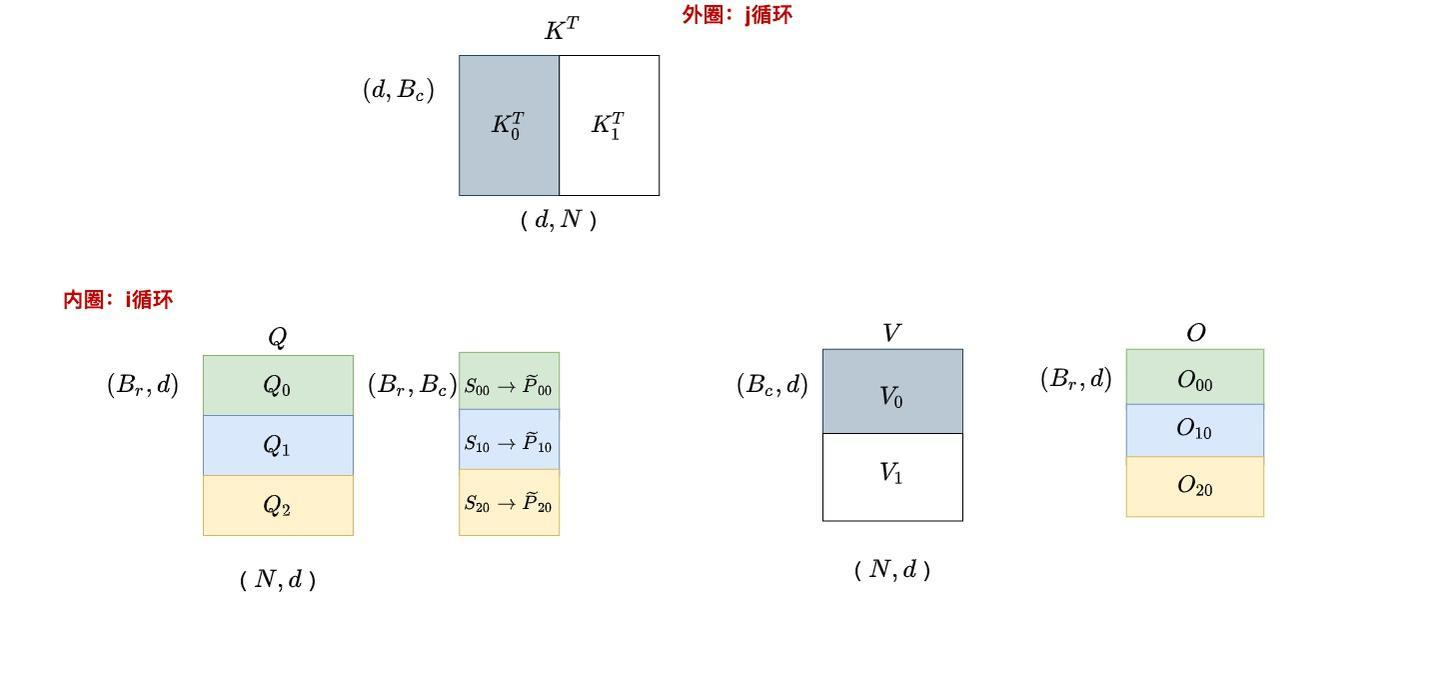
外循环：遍历K、V的分块（j方向）
内循环：遍历Q的分块（i方向）

j=0，这遍历i
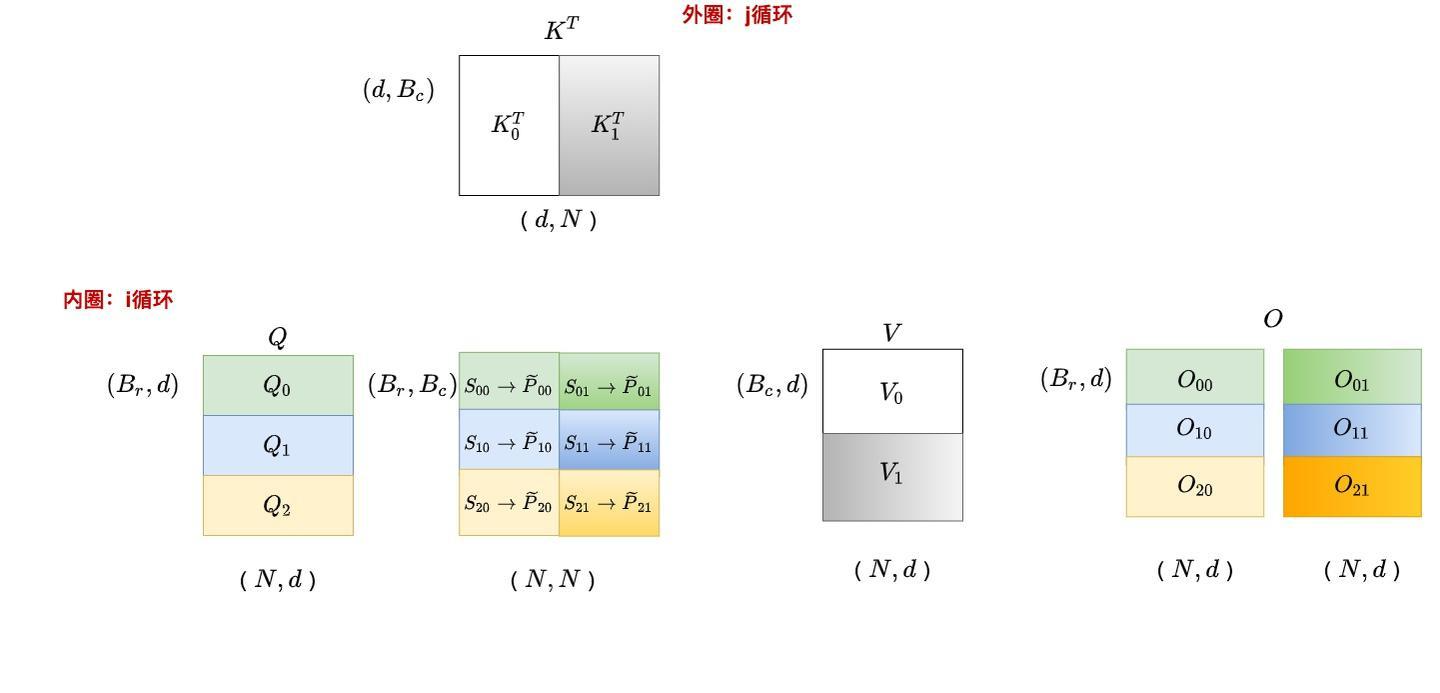
在这里插入图片描述

j=1，这遍历i
在这里插入图片描述

具体流程：

将Q、K、V分别分割成多个块
外层循环遍历K、V的每个块
内层循环遍历Q的每个块
计算部分注意力分数并累积结果

1.3 在线softmax算法

为了处理分块计算中的softmax，V1使用了在线softmax算法：

# 在线softmax的核心公式
def online_softmax_update(old_max, old_sum, new_values):new_max = max(old_max, max(new_values))correction_factor = exp(old_max - new_max)old_sum *= correction_factornew_sum = old_sum + sum(exp(new_values - new_max))return new_max, new_sum

关键变量：

m_i^{(j)}: 当前分块的行最大值
ℓ_i^{(j)}: 当前分块的行和
O_i^{(j)}: 当前分块的输出累积值

二、Flash Attention V2的核心改进

在这里插入图片描述

2.1 循环顺序的调整

V2最重要的改进是交换了内外循环的顺序：

外循环：遍历Q的分块（i方向）
内循环：遍历K、V的分块（j方向）

这个看似简单的调整带来了显著的性能提升，原因在于：

数据局部性改进

固定Q块，遍历K、V块的方式更符合softmax的行计算特性。每一行的softmax计算可以一次性完成，避免了中间状态的反复存储和读取。

内存访问模式优化

# V1的访问模式
for j in range(num_kv_blocks):load_kv_block(j)for i in range(num_q_blocks):load_q_block(i)compute_attention_block(i, j)save_intermediate_results(i)# V2的访问模式  
for i in range(num_q_blocks):load_q_block(i)initialize_output(i)for j in range(num_kv_blocks):load_kv_block(j)update_output_incrementally(i, j)finalize_output(i)

2.2 Forward Pass算法详解

V2的前向传播算法可以表示为以下伪代码：

def flash_attention_v2_forward(Q, K, V):# 分块参数Tr = ceil(N / Br)  # Q块数量Tc = ceil(N / Bc)  # K,V块数量# 初始化输出O = zeros((N, d))L = zeros(N)  # log-sum-exp for numerical stability# Q分块的外循环for i in range(Tr):# 从HBM加载Q块到SRAMQi = load_q_block(i)# 初始化当前Q块的累积值Oi = zeros((Br, d))mi = fill(-inf, Br)  # 行最大值li = zeros(Br)       # 行和# K,V分块的内循环for j in range(Tc):# 从HBM加载K,V块到SRAMKj, Vj = load_kv_block(j)# 计算注意力分数Sij = Qi @ Kj.T  # (Br, Bc)# 更新行最大值mi_new = element_wise_max(mi, row_max(Sij))# 计算概率矩阵（未归一化）Pij_tilde = exp(Sij - mi_new[:, None])# 更新行和correction = exp(mi - mi_new)li = correction * li + row_sum(Pij_tilde)# 更新输出Oi = diag(correction) @ Oi + Pij_tilde @ Vj# 更新行最大值mi = mi_new# 最终归一化Oi = diag(1/li) @ Oi# 保存到HBMsave_output_block(i, Oi)Li = mi + log(li)  # 保存log-sum-expsave_lse_block(i, Li)return O, L

2.3 关键数学公式

V2中的核心更新公式：

行最大值更新

$m_i^{(j)} = max(m_i^{(j-1)}, rowmax(S_ij))$

概率矩阵计算

$P̃_ij = exp(S_ij - m_i^{(j)})$

行和更新

$ℓ_i^{(j)} = e^{m_i^{(j-1)} - m_i^{(j)}} · ℓ_i^{(j-1)} + rowsum(P̃_ij)$

输出更新

$O_i^{(j)} = diag(e^{m_i^{(j-1)} - m_i^{(j)}}) · O_i^{(j-1)} + P̃_ij V_j$

2.4 Backward Pass的循环策略

在这里插入图片描述

有趣的是，V2在反向传播中又采用了V1的循环顺序（KV外循环，Q内循环）。这是因为：

梯度计算的特性：
- dK, dV需要沿i方向累加（行累加）
- dQ需要沿j方向累加（列累加）
- 采用KV外循环对dK, dV更有利

数据读写优化：

# V2 Backward的访问模式
for j in range(num_kv_blocks):load_kv_block(j)initialize_gradients_kv(j)for i in range(num_q_blocks):load_q_block(i)load_intermediate_values(i)compute_gradients(i, j)accumulate_dK_dV(j)update_dQ(i)

三、V2的并行优化策略

3.1 Thread Block级别的并行

V1的并行策略

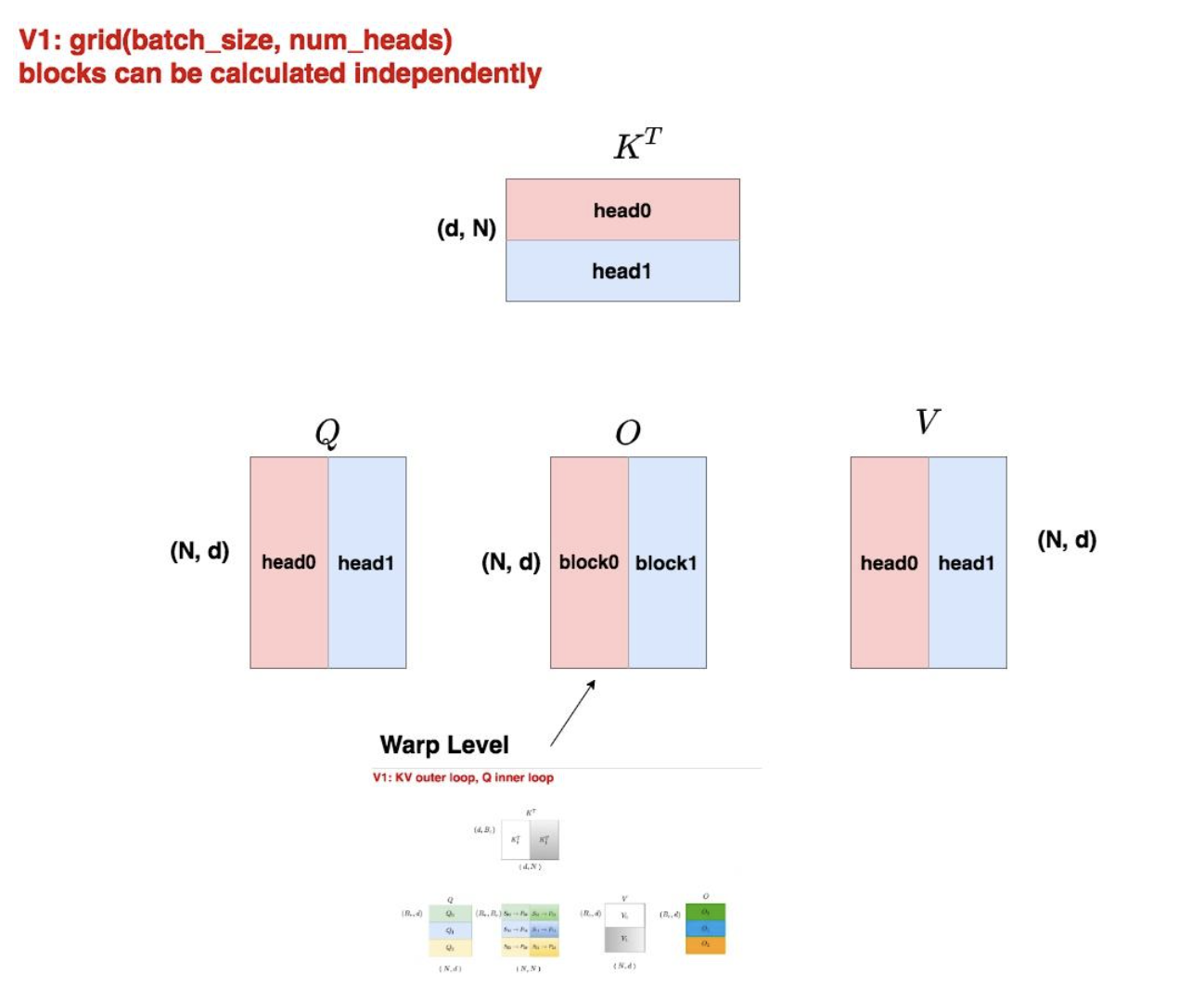
在这里插入图片描述

# V1的grid配置
grid = (batch_size, num_heads)

每个thread block负责一个完整的attention head计算。

V2的并行策略

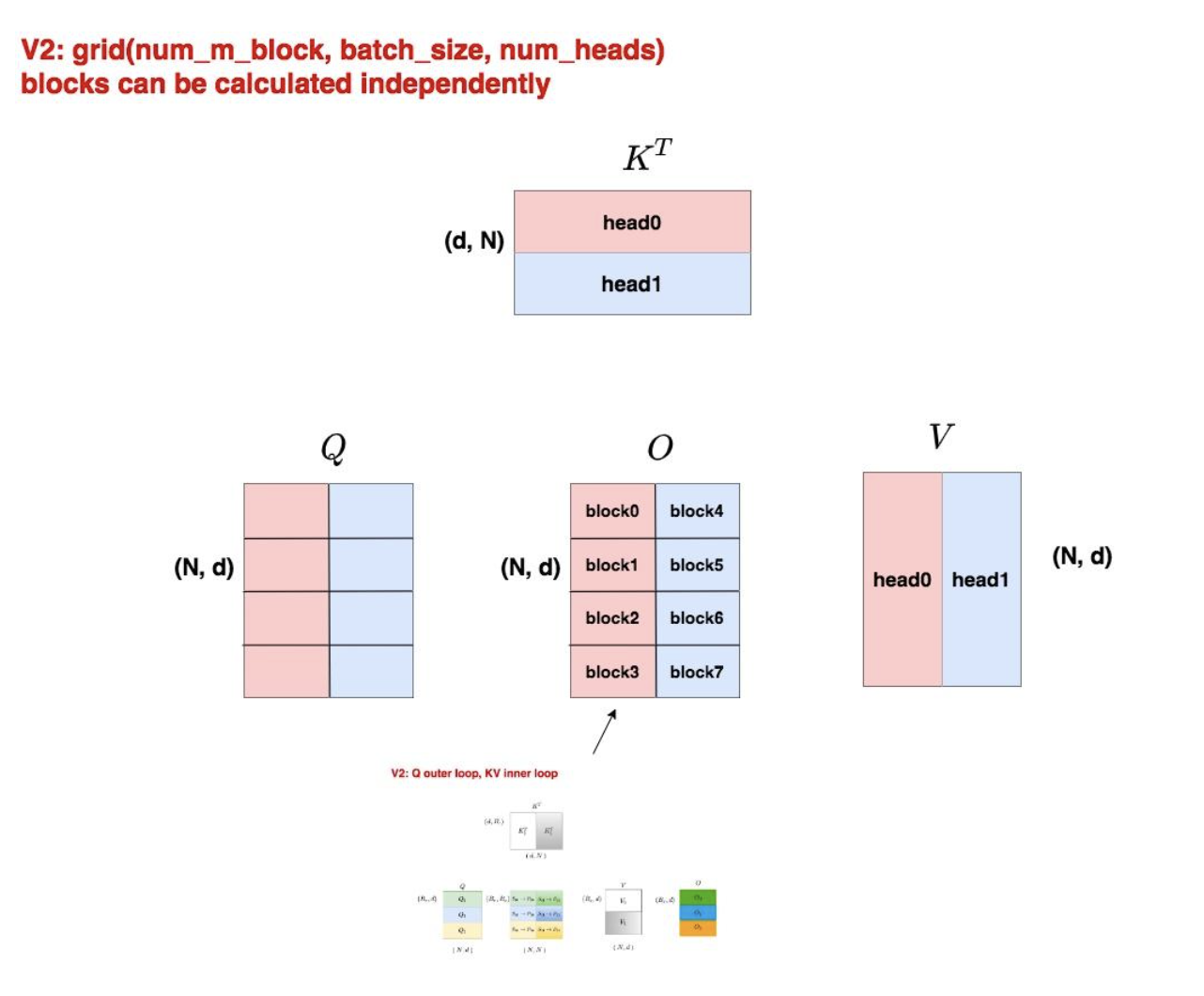
在这里插入图片描述

# V2的grid配置
num_m_block = (seq_len_q + block_size - 1) // block_size
grid = (num_m_block, batch_size, num_heads)

V2在序列维度上也进行了并行分割，显著提升了SM（Streaming Multiprocessor）的利用率。

3.2 SM利用率分析

假设一个A100 GPU有108个SM：

V1的利用情况

当batch_size=2, num_heads=8时，总共16个blocks
SM利用率 = 16/108 ≈ 14.8%

V2的利用情况

当seq_len=2048, block_size=64时，num_m_block=32
总block数 = 32 × 2 × 8 = 512个blocks
SM利用率接近100%

3.3 Cache友好性优化

V2调整了grid的维度顺序：(num_m_block, batch_size, num_heads)，这样同一列的blocks访问相同的K、V数据，提升了L2 cache命中率。

# Cache友好的访问模式示例
def cache_friendly_access():for col_idx in range(num_m_block):kv_data = load_kv_once()  # 多个blocks共享for batch in range(batch_size):for head in range(num_heads):process_block(col_idx, batch, head, kv_data)

四、Warp级别的工作分配

4.1 V1的Warp分配

在V1中，每个thread block内的4个warp（Ampere架构）按列分割工作：

每个warp处理输出矩阵的不同列
需要warp间通信来合并最终结果
存在shared memory的读写开销

4.2 V2的Warp分配

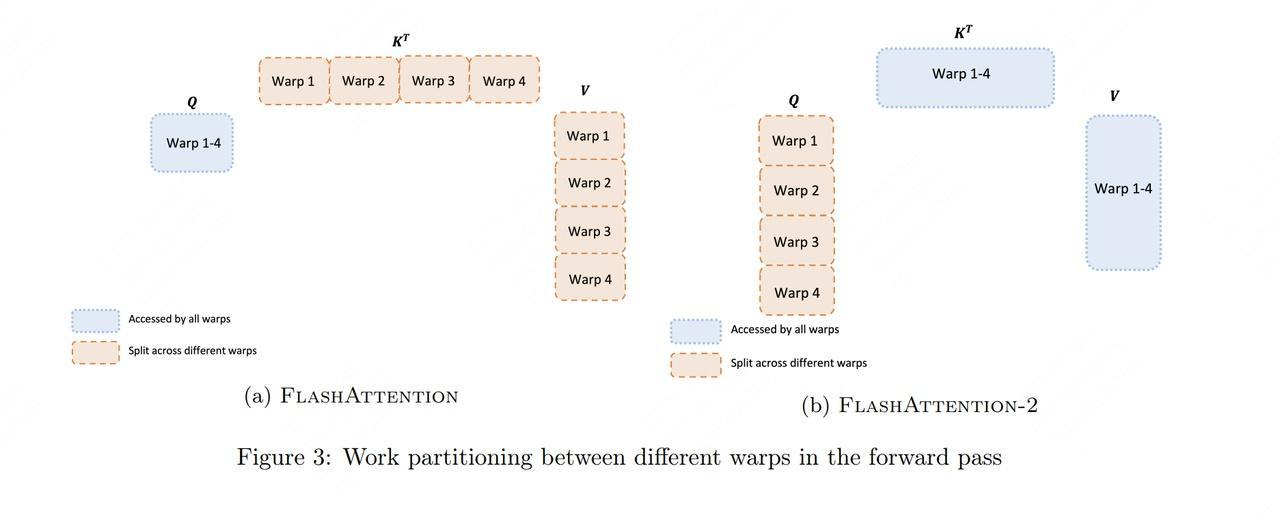
在这里插入图片描述
V2将工作按行分割：

每个warp处理输出矩阵的不同行
行间计算完全独立，无需warp间通信
减少了shared memory的使用

# V1的warp分配（列分割）
def v1_warp_distribution():shared_memory = allocate_shared_memory()for warp_id in range(4):partial_result = compute_columns(warp_id)shared_memory[warp_id] = partial_result# 需要同步和合并synchronize_warps()final_result = merge_results(shared_memory)# V2的warp分配（行分割）
def v2_warp_distribution():for warp_id in range(4):row_result = compute_rows(warp_id)# 直接写入最终位置，无需合并write_output(warp_id, row_result)

五、非矩阵运算的优化

V2特别强调减少非矩阵运算（non-matmul FLOPs），因为在GPU上，非矩阵运算比矩阵运算慢约16倍。

5.1 归一化操作的延迟

# V1的做法：每次都做归一化
def v1_normalization():for j in range(num_blocks):Pij = compute_attention_scores(i, j)Pij_normalized = Pij / rowsum(Pij)  # 每次都归一化Oi += Pij_normalized @ Vj# V2的做法：延迟到最后统一归一化
def v2_normalization():for j in range(num_blocks):Pij_unnormalized = compute_attention_scores(i, j)Oi += Pij_unnormalized @ Vj  # 累积未归一化的结果Oi = Oi / final_normalizer  # 最后统一归一化

5.2 中间状态存储的简化

V2只存储一个关键量：LSE = m + log(ℓ)（log-sum-exp），而不是分别存储m和ℓ，减少了内存读写。

六、代码实现示例

基于以上原理，我们可以实现一个简化版的Flash Attention V2：

import torch
import math
from typing import Tupleclass FlashAttentionV2:def __init__(self, block_size_q: int = 64, block_size_kv: int = 64):self.Br = block_size_q    # Q的分块大小self.Bc = block_size_kv   # K,V的分块大小def forward(self, Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor) -> torch.Tensor:"""Flash Attention V2前向传播Args:Q: Query矩阵，shape (batch, heads, seq_len, d_head)K: Key矩阵，shape (batch, heads, seq_len, d_head)  V: Value矩阵，shape (batch, heads, seq_len, d_head)Returns:O: 输出矩阵，shape (batch, heads, seq_len, d_head)"""batch_size, num_heads, seq_len, d_head = Q.shapedevice = Q.device# 计算分块数量Tr = math.ceil(seq_len / self.Br)  # Q分块数量Tc = math.ceil(seq_len / self.Bc)  # K,V分块数量# 初始化输出矩阵O = torch.zeros_like(Q)# 缩放因子scale = 1.0 / math.sqrt(d_head)# Q分块的外循环（V2的关键改进）for i in range(Tr):# 计算当前Q块的索引范围start_q = i * self.Brend_q = min((i + 1) * self.Br, seq_len)# 加载Q块Qi = Q[:, :, start_q:end_q, :]  # (batch, heads, Br, d_head)# 初始化当前Q块的累积状态block_size_q = end_q - start_q# 行最大值，初始化为负无穷mi = torch.full((batch_size, num_heads, block_size_q), float('-inf'), device=device)# 行和，初始化为0li = torch.zeros((batch_size, num_heads, block_size_q), device=device)# 输出累积值，初始化为0Oi = torch.zeros((batch_size, num_heads, block_size_q, d_head), device=device)# K,V分块的内循环for j in range(Tc):# 计算当前K,V块的索引范围start_kv = j * self.Bcend_kv = min((j + 1) * self.Bc, seq_len)# 加载K,V块Kj = K[:, :, start_kv:end_kv, :]  # (batch, heads, Bc, d_head)Vj = V[:, :, start_kv:end_kv, :]  # (batch, heads, Bc, d_head)# 计算注意力分数 Sij = Qi @ Kj.TSij = torch.matmul(Qi, Kj.transpose(-2, -1)) * scale# Shape: (batch, heads, Br, Bc)# 计算当前块的行最大值mij = torch.max(Sij, dim=-1, keepdim=False)[0]  # (batch, heads, Br)# 更新全局行最大值mi_new = torch.maximum(mi, mij)# 计算概率矩阵（未归一化）Pij_tilde = torch.exp(Sij - mi_new.unsqueeze(-1))# 计算当前块的行和lij = torch.sum(Pij_tilde, dim=-1)  # (batch, heads, Br)# 计算修正因子correction = torch.exp(mi - mi_new)# 更新行和li_new = correction * li + lij# 更新输出累积值# 首先对旧的输出应用修正因子Oi = Oi * correction.unsqueeze(-1)# 然后加上当前块的贡献Oi = Oi + torch.matmul(Pij_tilde, Vj)# 更新状态变量mi = mi_newli = li_new# 最终归一化Oi = Oi / li.unsqueeze(-1)# 将结果写入输出矩阵O[:, :, start_q:end_q, :] = Oireturn O# 使用示例和测试
def test_flash_attention_v2():"""测试Flash Attention V2的实现"""batch_size = 2num_heads = 8  seq_len = 512d_head = 64device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')# 生成随机输入Q = torch.randn(batch_size, num_heads, seq_len, d_head, device=device)K = torch.randn(batch_size, num_heads, seq_len, d_head, device=device)V = torch.randn(batch_size, num_heads, seq_len, d_head, device=device)# Flash Attention V2flash_attn = FlashAttentionV2(block_size_q=64, block_size_kv=64)output_flash = flash_attn.forward(Q, K, V)# 标准注意力（用于对比）def standard_attention(Q, K, V):scale = 1.0 / math.sqrt(Q.size(-1))scores = torch.matmul(Q, K.transpose(-2, -1)) * scaleattn_weights = torch.softmax(scores, dim=-1)output = torch.matmul(attn_weights, V)return outputoutput_standard = standard_attention(Q, K, V)# 计算误差max_error = torch.max(torch.abs(output_flash - output_standard))mean_error = torch.mean(torch.abs(output_flash - output_standard))print(f"最大误差: {max_error.item():.6f}")print(f"平均误差: {mean_error.item():.6f}")print(f"相对误差: {(mean_error / torch.mean(torch.abs(output_standard))).item():.6f}")# 验证形状assert output_flash.shape == output_standard.shapeprint("形状验证通过!")if __name__ == "__main__":test_flash_attention_v2()

七、主流大模型中Flash Attention的应用

7.1 开源模型的支持情况

目前大多数主流开源模型都支持Flash Attention，通常通过以下方式集成：

Llama系列

Llama 3.1: 原生支持Flash Attention 2，在transformers库中可通过attn_implementation="flash_attention_2"启用
Llama 3.2: 同样支持Flash Attention 2，特别优化了长上下文场景
Llama 3.3: 延续了对Flash Attention 2的支持

# Llama模型启用Flash Attention的示例
from transformers import LlamaForCausalLMmodel = LlamaForCausalLM.from_pretrained("meta-llama/Llama-3.1-7B",attn_implementation="flash_attention_2",torch_dtype=torch.float16,device_map="auto"
)