【LeetCode hot100|Week2】滑动窗口，子串

笔记用于个人复习和巩固，题解非原创，参考LeetCode官方题解以及各个大佬的解法，希望给大家带来帮助，同时笔记也能督促我学习进步

这周主要把滑动窗口和子串的题目刷了一遍

Week2

D1 滑动窗口

只有当数组中所有数都是非负数时，才能使用滑动窗口。

如果数组中包含负数不能使用标准的滑动窗口

滑动窗口的核心前提：

当窗口扩大时，和变大；窗口缩小时，和变小。

209. 长度最小的子数组

209. 长度最小的子数组

class Solution {public int minSubArrayLen(int target, int[] nums) {int n = nums.length;int ans = n + 1;int sum = 0;int left = 0;for(int right = 0;right < n;right++){sum += nums[right];while(sum >= target){ans = Math.min(ans,right - left + 1);sum -= nums[left];left++;}}return ans <= n ? ans : 0;}
}

713. 乘积小于 K 的子数组

713. 乘积小于 K 的子数组

class Solution {public int numSubarrayProductLessThanK(int[] nums, int k) {if(k <= 1){return 0;}int n = nums.length;int ans = 0;int prod = 1;int left = 0;for(int right = 0;right < n;right++){prod *= nums[right];while(prod >= k){ //不满足要求prod /= nums[left];left++; //缩小窗口}ans += right - left + 1;}return ans;}
}

3. 无重复字符的最长子串

3. 无重复字符的最长子串

class Solution {public int lengthOfLongestSubstring(String S) {char[] s = S.toCharArray();int ans = 0;int n = s.length;int left = 0;int[] cnt = new int[128];for(int right = 0;right < n;right++){char c = s[right];cnt[c]++;while(cnt[c] > 1){ //窗口有重复字符cnt[s[left]]--;//移除窗口左端点字符left++;//缩小窗口}ans = Math.max(ans,right - left + 1);}return ans;}
}

D2 定长滑窗&不定长滑窗

定长滑窗

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int n = s.length(); //测量String的长度用.length()int[] cntP = new int[26]; //统计p的每种字母的出现次数int[] cntS = new int[26]; //统计s的长为p.length()的子串s'的每种字母的出现次数for(char c:p.toCharArray()){cntP[c - 'a']++;}for(int right = 0;right < n;right++){cntS[s.charAt(right) - 'a']++;int left = right - p.length() + 1;if(left < 0){continue; //窗口长度不够}if(Arrays.equals(cntS,cntP)){ans.add(left);}cntS[s.charAt(left) - 'a']--; //左端字母离开窗口}return ans;}
}

Arrays.equals(cntS, cntP) 是 Java 中用来 判断两个数组是否“完全相同” 的标准方法

✅ 它比较的是：

两个数组在以下方面是否完全一致：

比较项	是否比较
1. 数组长度	是
2. 每个对应位置的元素值	是
3. 元素顺序	是（顺序不同 → 不相等）

如果以上全部相同，返回 true；否则返回 false。

---

定长滑窗套路

窗口右端点在 i 时，由于窗口长度为 k，所以窗口左端点为 i−k+1。

三步：入-更新-出

1. 入：下标为 i 的元素进入窗口，更新相关统计量。如果窗口左端点 i−k+1<0，则尚未形成第一个窗口，重复第一步。
2. 更新：更新答案。一般是更新最大值/最小值。
3. 出：下标为 i−k+1 的元素离开窗口，更新相关统计量，为下一个循环做准备。

不定长滑窗

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int[] cnt = new int[26]; // 统计 p 的每种字母的出现次数for (char c : p.toCharArray()) {cnt[c - 'a']++; //s中出现就-- 若cnt<0则说明子串c太多 }int left = 0;for (int right = 0; right < s.length(); right++) {int c = s.charAt(right) - 'a';cnt[c]--; // 右端点字母进入窗口while (cnt[c] < 0) { // 字母 c 太多了cnt[s.charAt(left) - 'a']++; // 左端点字母离开窗口left++;}if (right - left + 1 == p.length()) { // s' 和 p 的每种字母的出现次数都相同ans.add(left); // s' 左端点下标加入答案}}return ans;}
}

代码实现时，可以把 cntS 和 cntP 合并成一个 cnt：

• 对于 p 的字母 c，把 cnt[p] ++

• 对于 s’ 的字母 c，把 cnt[c] –

• 如果 cnt[c]<0，说明窗口中的字母 c 的个数比 p 的多，右移左端点。

D3

560. 和为 K 的子数组

560. 和为 K 的子数组

暴力

遍历得到所有子串并求和 筛选出符合条件的

class Solution {public int subarraySum(int[] nums, int k) {int ans = 0;int n = nums.length;for(int i = 0;i < n;i++){  //列举每个元素当子串结尾的情况int sum = 0;for(int j = i;j >= 0;j--){  //求所有以这个子串为结尾的和sum += nums[j];if(sum == k)ans++;}}return ans;}
}

前缀和+哈希表

前缀和：pre[i]=pre[i−1]+nums[i]

[j…i] 这个子数组和为 k 这个条件我们可以转化为pre[i]−pre[j−1]==k

简单移项可得符合条件的下标 j 需要满足

pre[j−1]==pre[i]−k

class Solution {public int subarraySum(int[] nums, int k) {int ans = 0,pre = 0;int n = nums.length;HashMap<Integer,Integer>mp = new HashMap<>();mp.put(0,1);for(int i = 0;i < n;i++){pre += nums[i];if(mp.containsKey(pre - k)){ans += mp.get(pre - k);}mp.put(pre,mp.getOrDefault(pre,0) + 1);}return ans;}
}

D4

239. 滑动窗口最大值

239. 滑动窗口最大值

单调队列

单调队列套路

1. 右边入（元素进入队尾，同时维护队列单调性）
2. 左边出（元素离开队首）
3. 记录/维护答案（根据队首）

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;int[] ans = new int[n - k + 1]; // 窗口个数Deque<Integer> q = new ArrayDeque<>(); // 更快的写法见【Java 数组】for (int i = 0; i < n; i++) {// 1. 右边入while (!q.isEmpty() && nums[q.getLast()] <= nums[i]) {q.removeLast(); // 维护 q 的单调性}q.addLast(i); // 注意保存的是下标，这样下面可以判断队首是否离开窗口// 2. 左边出int left = i - k + 1; // 窗口左端点if (q.getFirst() < left) { // 队首离开窗口q.removeFirst();}// 3. 在窗口左端点处记录答案if (left >= 0) {// 由于队首到队尾单调递减，所以窗口最大值就在队首ans[left] = nums[q.getFirst()];}}return ans;}
}

D5

76. 最小覆盖子串

76. 最小覆盖子串

class Solution {public String minWindow(String S, String t) {int[] cntS = new int[128]; // s 子串字母的出现次数int[] cntT = new int[128]; // t 中字母的出现次数for (char c : t.toCharArray()) {cntT[c]++;}char[] s = S.toCharArray();int m = s.length;int ansLeft = -1;int ansRight = m;int left = 0;for (int right = 0; right < m; right++) { // 移动子串右端点cntS[s[right]]++; // 右端点字母移入子串 如果 s[right] 是一个 char 类型的字符，它会被自动转换成对应的 ASCII/Unicode 数值（int），然后作为数组下标使用while (isCovered(cntS, cntT)) { // 涵盖if (right - left < ansRight - ansLeft) { // 找到更短的子串ansLeft = left; // 记录此时的左右端点ansRight = right;}cntS[s[left]]--; // 左端点字母移出子串left++;}}return ansLeft < 0 ? "" : S.substring(ansLeft, ansRight + 1);}private boolean isCovered(int[] cntS, int[] cntT) {for (int i = 'A'; i <= 'Z'; i++) {if (cntS[i] < cntT[i]) {return false;}}for (int i = 'a'; i <= 'z'; i++) {if (cntS[i] < cntT[i]) {return false;}}return true;}
}

D6

53. 最大子数组和

53. 最大子数组和

贪心

若指针所指当前元素之前的和小于0，则丢弃当前元素之前的数列

class Solution {public int maxSubArray(int[] nums) {int pre = 0, ans = nums[0];for (int x : nums) {if(pre < 0){pre = x;}else{pre += x;}ans = Math.max(pre,ans);}return ans;}
}

动态规划

考虑 nums[i] 单独成为一段还是加入 f(i−1) 对应的那一段，这取决于 nums[i] 和f(i−1)+nums[i] 的大小

class Solution {public int maxSubArray(int[] nums) {int pre = 0, maxAns = nums[0];for (int x : nums) {pre = Math.max(pre + x, x);maxAns = Math.max(maxAns, pre);}return maxAns;}
}

D7

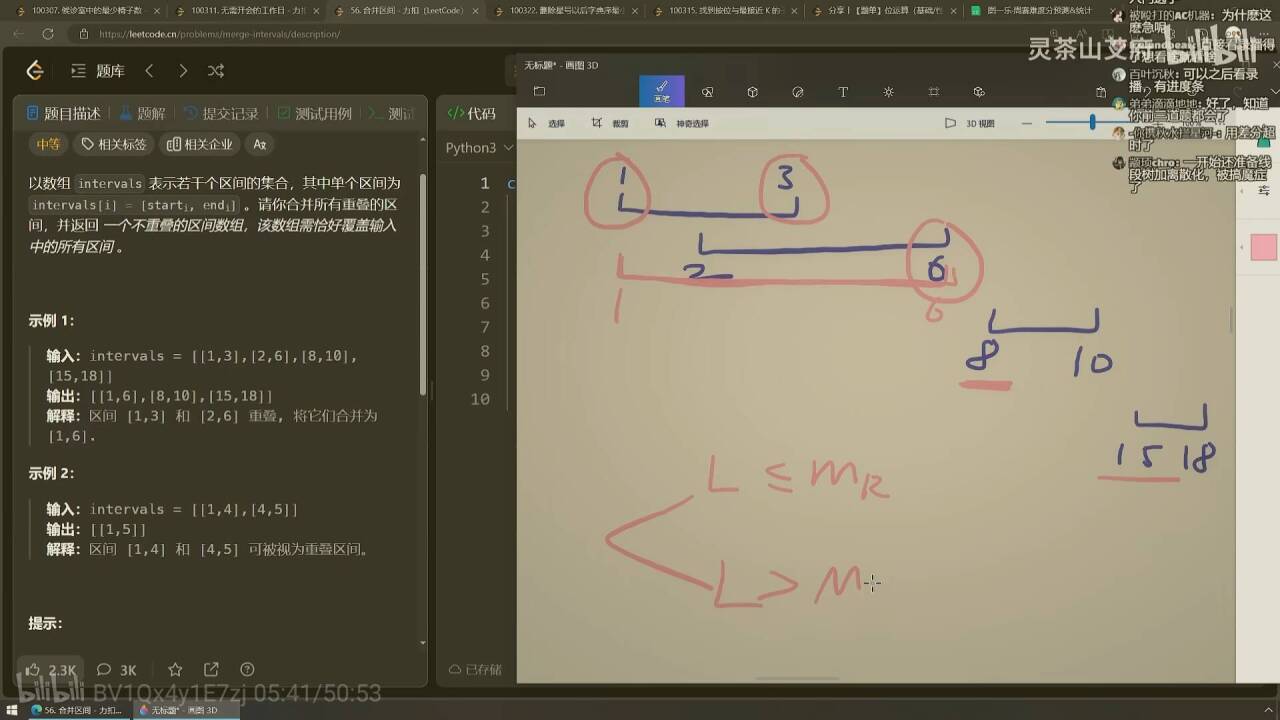
56. 合并区间

56. 合并区间

一开始想到三种区间关系，覆盖，重叠，相离，不知道怎么把合并的区间添加到ans中

其实不用分出三种区间关系，直接判断能否合并就行，即前一个的right和后一个left的关系：

• q_left <= p_right 可以合并
• q_left > p_right 不可以合并

对于最后将合并好的区间添加的ans里也可以简单化：

• 可合并：添加前一个区间p进ans 修改p_right为q_right（如果q_right更大的话）
• 不可合并：直接将该区间加入
  

class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (p, q) -> p[0] - q[0]); // 按照左端点从小到大排序List<int[]> ans = new ArrayList<>(); //不知道最后结果大小 没法用二维数组for (int[] p : intervals) {int m = ans.size();if (m > 0 && p[0] <= ans.get(m - 1)[1]) { // 可以合并ans.get(m - 1)[1] = Math.max(ans.get(m - 1)[1], p[1]); // 更新右端点最大值} else { // 不相交，无法合并ans.add(p);}}return ans.toArray(new int[ans.size()][]);}
}

return ans.toArray(new int[ans.size()][]);

作用是：将 List<int[]> 转换为 int[][]（二维数组）并返回。

为什么要写这一行？

• 函数的返回类型是 int[][]（二维数组）
• 但我们使用 List<int[]> 来动态存储合并后的区间（因为 List 可以随时 add，而数组大小固定）

所以，在最后必须把 List 转成 int[][] 才能返回。