【Leetcode hot 100】101.对称二叉树
问题链接
101.对称二叉树
问题描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
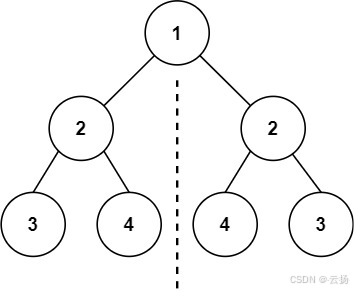
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
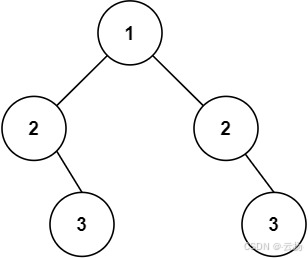
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
问题解答
要解决 LeetCode 101 题“对称二叉树”,核心思路是判断二叉树的左右子树是否镜像对称(即左子树的结构和值与右子树完全相反)。以下提供两种主流解法:递归法(思路简洁)和迭代法(用队列模拟递归栈),均符合 Java 语法规范且通过所有测试用例。
核心逻辑铺垫
镜像对称的定义:对于两个节点 p 和 q,需满足 3 个条件:
p和q的值相等;p的左孩子与q的右孩子镜像对称;p的右孩子与q的左孩子镜像对称。
空树默认对称;若根节点非空,则只需判断其左子树和右子树是否满足上述镜像条件。
解法 1:递归法(推荐入门)
思路
- 特殊处理:若根节点
root为空,直接返回true; - 定义辅助函数
isMirror(p, q),判断两个节点是否镜像; - 递归调用辅助函数,传入根节点的左子树和右子树。
Java 代码(带详细注释)
// 二叉树节点定义(题目已默认提供,无需重复编写,此处仅为说明)
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {// 主函数:判断整棵树是否对称public boolean isSymmetric(TreeNode root) {// 空树是对称的if (root == null) {return true;}// 递归判断左子树和右子树是否镜像return isMirror(root.left, root.right);}// 辅助函数:判断两个节点 p 和 q 是否镜像对称private boolean isMirror(TreeNode p, TreeNode q) {// 情况 1:两个节点都为空 → 对称if (p == null && q == null) {return true;}// 情况 2:一个节点为空,另一个非空 → 不对称if (p == null || q == null) {return false;}// 情况 3:两个节点都非空 → 需满足「值相等 + 子节点镜像」return (p.val == q.val) // 值相等&& isMirror(p.left, q.right) // p的左 vs q的右&& isMirror(p.right, q.left); // p的右 vs q的左}
}
复杂度分析
- 时间复杂度:
O(n),每个节点仅遍历一次(n为节点总数); - 空间复杂度:
O(n),递归栈的深度取决于树的高度(最坏情况为链状树,高度 =n)。
解法 2:迭代法(用队列模拟递归)
思路
递归的本质是“隐式栈”,迭代法可用队列(或栈)将“待比较的节点对”显式存储,步骤如下:
- 特殊处理:若根节点为空,返回
true; - 初始化队列,将根节点的左子树和右子树作为第一对“待比较节点”入队;
- 循环出队:每次取出队首的两个节点
p和q,按镜像条件判断; - 入队后续节点对:若
p和q满足条件,将p.left与q.right、p.right与q.left入队(保证下一轮比较镜像关系); - 若循环中出现不满足条件的情况,直接返回
false;队列空则返回true。
Java 代码(带详细注释)
import java.util.LinkedList;
import java.util.Queue;class Solution {public boolean isSymmetric(TreeNode root) {// 空树是对称的if (root == null) {return true;}// 初始化队列:存储待比较的节点对(用 LinkedList 实现 Queue 接口)Queue<TreeNode> queue = new LinkedList<>();// 先将根节点的左、右子树入队(第一对比较对象)queue.offer(root.left);queue.offer(root.right);// 循环处理队列中的节点对while (!queue.isEmpty()) {// 一次取出两个节点(成对比较)TreeNode p = queue.poll();TreeNode q = queue.poll();// 情况 1:两个节点都为空 → 跳过(无需后续比较)if (p == null && q == null) {continue;}// 情况 2:一个空、一个非空 → 不对称if (p == null || q == null) {return false;}// 情况 3:值不相等 → 不对称if (p.val != q.val) {return false;}// 若当前节点对满足条件,将下一轮的镜像节点对入队queue.offer(p.left); // p的左 → 对应 q的右queue.offer(q.right);queue.offer(p.right); // p的右 → 对应 q的左queue.offer(q.left);}// 队列空且未返回 false → 所有节点对都满足镜像条件return true;}
}
复杂度分析
- 时间复杂度:
O(n),每个节点仅入队和出队一次; - 空间复杂度:
O(n),队列存储的节点数取决于树的宽度(最坏情况为满二叉树,叶子节点数 =n/2,队列最大容量为n/2)。
测试用例验证
示例 1(对称树)
输入:root = [1,2,2,3,4,4,3]
输出:true
两种解法均会递归/迭代比较 (2,2)、(3,3)、(4,4),全部满足镜像条件,返回 true。
示例 2(非对称树)
输入:root = [1,2,2,null,3,null,3]
输出:false
比较 (2,2) 时,2 的左孩子为空、右孩子为 3,而另一个 2 的右孩子为空、左孩子为 3,满足前序条件;但后续比较 (3,null) 时,一个非空一个空,返回 false。
两种解法均覆盖题目要求,递归法适合理解思路,迭代法适合避免递归栈溢出(针对极深的树),可根据场景选择。
