当前位置：首页 > news >正文

算法提升之树形数据结构

news 2025/9/14 9:07:39

今天给大家详细来讲讲关于树状树形，线段树以及线段树上二分之间的关系和区别。

1.树状树形：可以实现单点的修改（结点），以及区间的查询，时间复杂度都是logn。

2.线段树：实现区间的修改和区间的查询，复杂度也是logn。

3.线段树上二分：处理大小排序，注意要做离散化的处理，然后存储的是数组内元素出现的个数。

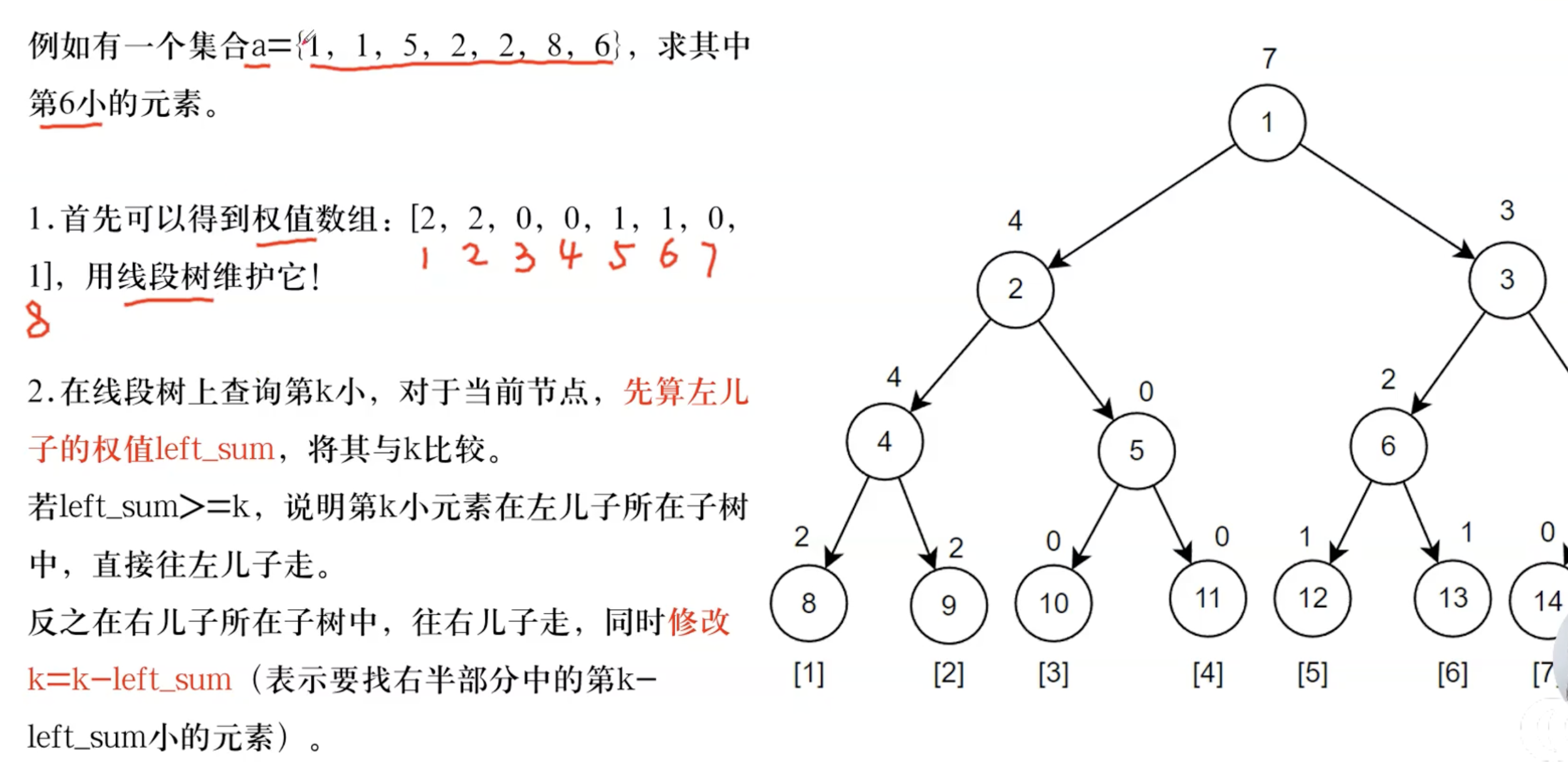
然后我通过一道题来帮助大家更好地理解有关线段树上二分的相关内容。

问题描述

小蓝最喜欢的学科是体育课。每节体育课都会以热身操开始。为了使热身操更有趣，也为了让学生们更加投入，体育老师会要求学生们按照身高顺序站成一排，并从中选出站在队伍中间的学生作为领队带头热身。如果有两个学生站在中间，他会选择较矮的那个。例如：

如果学生们的身高为 1、3、5、7、11，则身高为 5的学生将被选中带领热身操。
如果学生们的身高为 1、3、7、11，则身高为 3的学生将被选中带领热身操。

小蓝想要更好地参与体育课，对此，他希望自己能准确得知热身操领队学生的身高情况。

小蓝的朋友小桥很擅长估算人们的身高，他会给小蓝 n 条信息，每条信息的内容形式为：“有 ai 个身高为 vi 的学生进入了体育馆”。每当小桥说完一条信息后，小蓝都想知道，如果当前进入体育馆的学生都是来上体育课的，那么带领热身操的学生的身高会是多少。

请你帮助小蓝解答问题。

输入格式

第一行包含一个整数 n（1≤n≤2×105），表示小桥给出的信息条数。

接下来的 n行，每行包含两个整数 vi 和 ai（1≤vi,ai≤109），其含义如题所述。

输出格式

输出 n 行，每行一个整数。第 i行输出对应小桥给出第 i条信息后：在当前进入体育馆的学生都是来上体育课的情况下，带领热身操的学生的身高。

输入案例：

输出案例：

2
2
2

代码部分：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;int n;
const int N = 1e6;
struct node{ll a,v;
}q[N];
ll t[4*N];//出现次数 
vector<int> L;void pushup(int o){t[o]=t[o<<1]+t[o<<1|1];
}
int getidx(ll x) {return lower_bound(L.begin(),L.end(),x)-L.begin()+1;
}
int getval(int idx) {return L[idx-1];
}
void update(int a,int v,int s=1,int e=L.size(),int o=1){if(s==e){t[o]+=a;return;}int mid=s+e>>1;if(v<=mid) update(a,v,s,mid,o<<1);if(v>=mid+1) update(a,v,mid+1,e,o<<1|1);pushup(o);
}
ll query(ll k,int s=1,int e=L.size(),int o=1){if(s==e){return s;}int mid=s+e>>1;ll left_sum=t[o<<1];if(left_sum>=k) return query(k,s,mid,o<<1);if(left_sum<k) return query(k-left_sum,mid+1,e,o<<1|1); 
}int main() {cin>>n;for(int i=1; i<=n; i++) {cin>>q[i].v>>q[i].a;}for(int i=1;i<=n;i++){L.push_back(q[i].v);    }sort(L.begin(),L.end());L.erase(unique(L.begin(),L.end()),L.end());ll sum=0;for(int i=1;i<=n;i++){update(q[i].a,getidx(q[i].v));sum+=q[i].a;cout<<getval(query((sum+1)/2))<<endl;}return 0;
}

1.L中存的是不重复身高的数据，而树中t存入的是不同身高的个数，要注意这两点的区别，不要弄混。

这个函数的作用是将原始身高值 x 映射到离散化后的索引，具体过程如下：

lower_bound(L.begin(), L.end(), x)：在排序后的数组 L 中查找第一个大于等于 x 的元素，返回该元素的迭代器（指针）。
减去 L.begin()：得到该元素在数组中的下标（从 0 开始）。
加 1：将下标转换为从 1 开始的索引（因为线段树通常习惯用 1 作为根节点和起始索引）。

举个例子：
假设 L = [1, 2, 3]（已排序去重）：

getidx(2)：lower_bound 找到元素 2，下标是 1，返回 1 + 1 = 2。
getidx(4)：lower_bound 返回 L.end()，下标是 3，返回 3 + 1 = 4（但这种情况在代码中不会出现，因为 x 一定是 L 中存在的值）。

这个函数的意义是：将原始身高值转换为线段树可以处理的索引（因为原始身高可能很大，无法直接作为数组下标）。

3.e=L.size()，注意离散化处理的效果，范围要控制好。

这是线段树上二分的主要思想和相关的代码内容，希望大家可以多多练习，相信对于大家这部分的学习还是非常有帮助的，后续我也会继续更新这一部分相关的有关代码题目。希望大家多多关注。