当前位置：首页 > news >正文

MX 模拟赛二总结

news 2025/9/14 8:45:11

哈哈，从来没想过还会再考一次 MX 的题……

T1

题面：

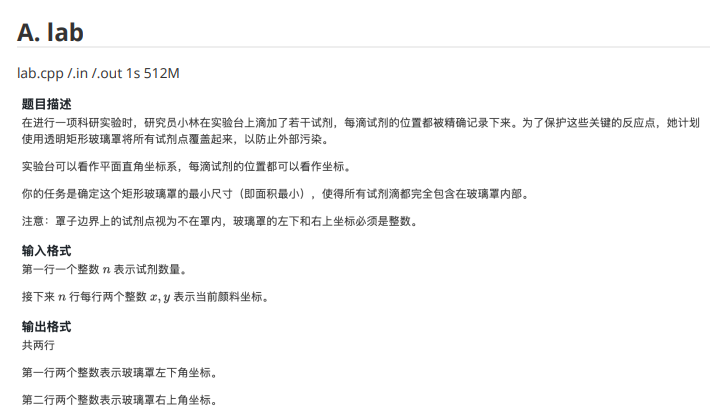
水到不能再水的题……大概就普及组第一题的难度。

代码自己写。

T2

题面：

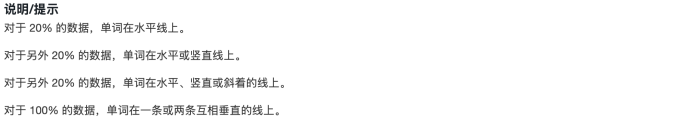
注意题中的两个限制：

其中一部分字母在一条直线上，另一部分字母在另一条直线上。
两个方向形成一个直角拐弯。

如果这题就是一个单纯的找单词，那还真不好写，但有了这两条限制，我相信还是很容易写出正解的吧……

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,m,len,ans,fx[8][2]={1,0,0,-1,-1,0,0,1,1,1,-1,1,-1,-1,1,-1},b[8][2]={1,3,0,2,1,3,0,2,5,7,4,6,5,7,4,6};
char mp[106][106];
string s;
void dfs(int x,int y,int id,int f,bool fl)
{if(id==len-1){ans++;return;}int xx=x+fx[f][0],yy=y+fx[f][1];if(xx<1||xx>n||yy<1||yy>m){if(!fl&&id!=0){dfs(x,y,id,b[f][0],1);dfs(x,y,id,b[f][1],1);}return;}if(mp[xx][yy]!=s[id+1]){if(fl||id==0){return;}dfs(x,y,id,b[f][0],1);dfs(x,y,id,b[f][1],1);}else{dfs(xx,yy,id+1,f,fl);if(fl||id==0){return;}dfs(x,y,id,b[f][0],1);dfs(x,y,id,b[f][1],1);}
}
signed main()
{
//	freopen("treasure.in","r",stdin);
//	freopen("treasure.out","w",stdout);cin>>s;cin>>n>>m;len=s.size();for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>mp[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(mp[i][j]==s[0]){for(int k=0;k<8;k++){dfs(i,j,0,k,0);}}}}cout<<ans;return 0;
}

时间复杂度： $O(2∣s∣nm)O(2\mid s\mid nm)$ ，其中 $∣s∣\mid s\mid$ 是字符串 $s$ 的长度，最多 $200$ 左右，所以暴搜直接过。

T3

题面：

其实就是一个循环的问题，先开始取个模，然后 $O (n)$ 扫一遍字符串看看到哪停止，比第二题代码都还短。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,sum;
string s;
signed main()
{
//	freopen("song.in","r",stdin);
//	freopen("song.out","w",stdout);cin>>s;n=s.size();for(int i=0;i<n;){if(s[i]<'0'||s[i]>'9'){i++;}else{int z=0;while(s[i]>='0'&&s[i]<='9'){z=z*10+s[i]-'0';i++;}sum+=z;}}int num;cin>>num;num++;num%=sum;if(num==0){num=sum;}string t;for(int i=0;i<n;){if(s[i]<'0'||s[i]>'9'){t+=s[i];i++;}else{int z=0;while(s[i]>='0'&&s[i]<='9'){z=z*10+s[i]-'0';i++;}if(num<=z){cout<<t;break;}t="";num-=z;}}return 0;
}

T4

题面：

首先讲一下 40pts 怎么拿。

不难看到：对于 $40%40\%$ 的数据， $N≤20N\le20$ 。这说明什么？说明我们可以暴力搜索啊！

那对于有两个变元的题我们怎么做啊？诶，先确定一个变元，再按照另一个变元算。我这里凭感觉选的先把 $b$ 从大到小排序。然后不难用反证法（即任意交换两个值看看是否比当前的解更优）证出当前的排序方法就是最优方案，然后我们就可以写暴力 dfs 了。

代码还是很好写的，建议自己实操一下。

然后我们来讲一下满分做法。

首先这里用了 dfs，那大概率可以逆推变成 DP 题。按照 dfs 的参数，我们可以设 dp[i][j] 表示前 $i$ 个人中在一号窗口的人的 $a$ 的和为 $j$ 时的最早时间。

于是我们可以写出状态转移方程：

$dp_{i,j}=\min(\max(dp_{i-1,j},s_i-j+b_i),\max(dp_{i-1,j-a_i},j+b_i))$

其中 $s_i$ 是 $a_i$ 的前缀和。

算一下空间复杂度：总共 $500$ 个数，每个数的大小不超过 $500$ ，所以空间复杂度最大 $500×500×500=1.25×108500\times500\times500=1.25\times10^8$ ，明显会超，所以这里使用滚动 DP 优化。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct pp{int x,y;
}a[506];
int n,dp[250006];
bool cmp(pp x,pp y)
{return x.y>y.y;
}
signed main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i].x>>a[i].y;}sort(a+1,a+n+1,cmp);int s=0;memset(dp,0x3f,sizeof(dp));dp[0]=0;for(int i=1;i<=n;i++){s+=a[i].x;for(int j=s;j>=0;j--){dp[j]=max(dp[j],s-j+a[i].y);if(j>=a[i].x){dp[j]=min(max(dp[j-a[i].x],j+a[i].y),dp[j]);}}}int ans=LONG_LONG_MAX;for(int i=0;i<=s;i++){ans=min(ans,dp[i]);}cout<<ans;return 0;
}

T5

题面：

首先对于前 $30%30\%$ 的数据可以直接用状压暴力算。

中间 $30%30\%$ 的数据用点组合数学的知识可以轻松解决。

现在来讲最后 $40%40\%$ 的数据怎么解决。

我们假设当前枚举到二进制下的第 $k$ 位，那第 $k$ 位是 $1$ 的数肯定不能全放在一个集合里面，因为如果全放在了一个集合里面，那另一个集合里面的数的运算结果在第 $k$ 上肯定不是 $1$ 。也就肯定不会和另一个集合相同。

那正面统计看上去太难了，我们就反着统计：看一看第 $k$ 位为 $1$ 的数全放在一个集合里的方案数是多少，然后整体减空白就对了。

那这题看上去似乎很简单啊，统计一下然后枚举一下二进制下的每一位就可以了啊。其实不是的，因为我们知道容斥原理，容斥原理中最重要的就是答案之间有重复，那这里明显也有可能有重复的情况啊，所以我们要用容斥原理来解决这道题。

那根据容斥原理里面的“奇加偶减”的原则，我们可以枚举 $i$ 表示当前算的是韦恩图中的哪一块，其中 $0≤i<2150\le i\lt2^{15}$ ，然后根据奇加偶减的原则得出：当 $i$ 在二进制下的 $1$ 的个数为奇数时加上当前的方案数，反之减去当前的方案数，然后因为我们要整体减空白，我们也可以反过来变成奇减偶加，这样就可以直接得出正确答案。

最后说一下这个每一种情况的答案怎么算：如果第 $k$ 位是 $1$ ，那我们就把这些数放在一个连通快里面，这可以用并查集来解决，最后看看有多少个连通块，其中每个连通块可以放在 A 集合也可以放在 B 集合，所以答案应该是 $2^{cnt}$ 个（ $c n t$ 表示连通块的数量）。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
#define pc __builtin_popcount
code by plh;
const int mod=998244353;
int n,ans,a[206],fa[206];
int find(int x)
{return fa[x]=(fa[x]==x?x:find(fa[x]));
}
int qpow(int x,int y)
{int z=1;while(y){if(y&1){z=(z*x)%mod;}x=(x*x)%mod;y>>=1;}return z;
}
signed main()
{int m=0;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];m|=a[i];}ans=qpow(2,n);for(int i=1;i<(1<<15);i++){if((i&m)!=i){continue;}for(int j=1;j<=n;j++){fa[j]=j;}for(int j=0;j<=14;j++){if(!(i&(1<<j))){continue;}int la=0;for(int k=1;k<=n;k++){if(!(a[k]&(1<<j))){continue;}if(!la){la=k;}fa[find(k)]=find(la);}}int num=0;for(int j=1;j<=n;j++){if(find(j)==j){num++;}}if(!(pc(i)&1)){ans=(ans+qpow(2,num))%mod;}else{ans=(ans-qpow(2,num)+mod)%mod;}}cout<<ans;return 0;
}