【LeetCode】杨辉三角，轮转数组，洗牌算法

杨辉三角

题目描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

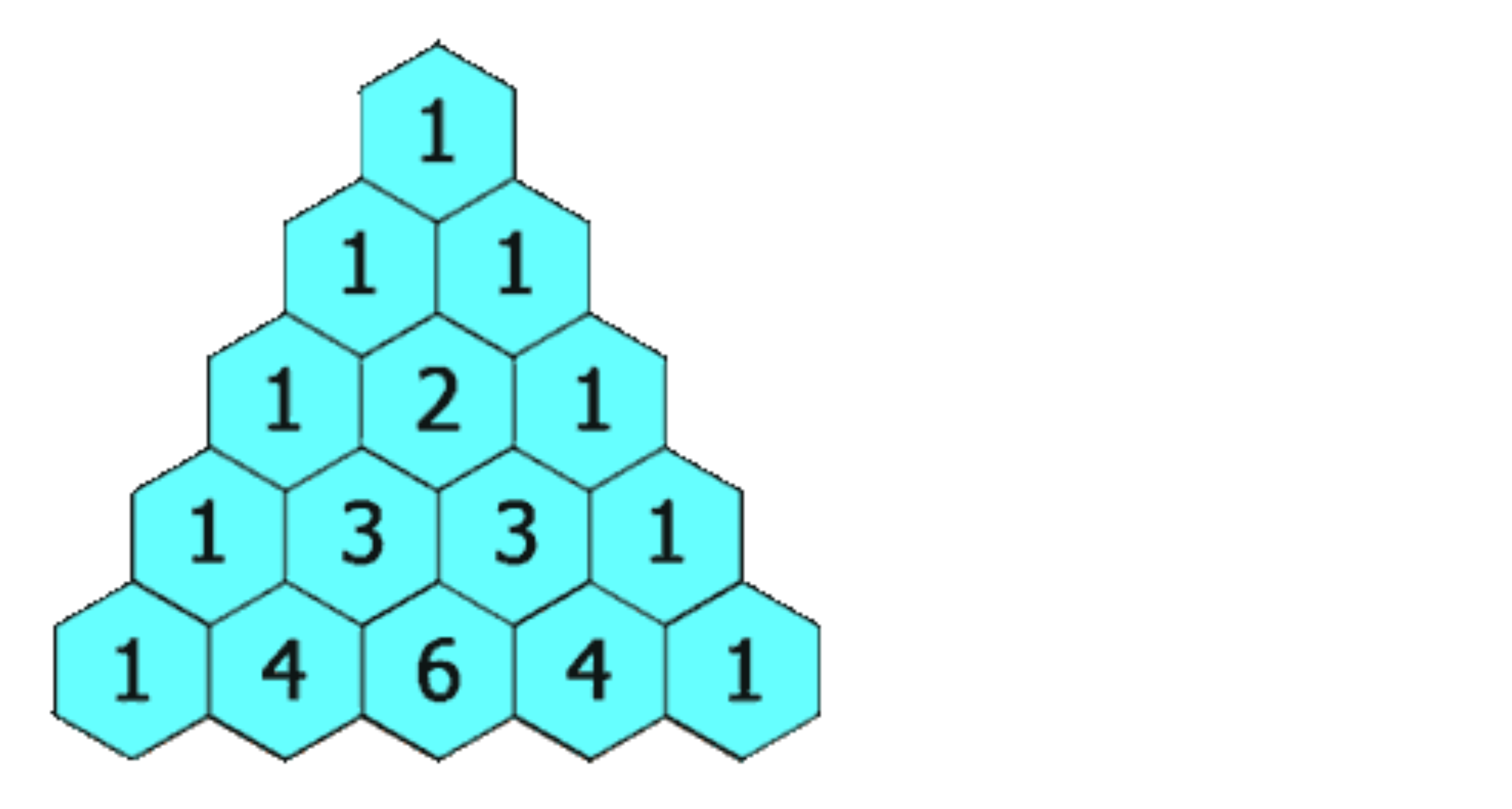
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:
输入: numRows = 1
输出: [[1]]

解题思路

1. 杨辉三角可以当做二维数组处理，每一层是一个List列表，整体由多层List列表构成。先定义二维列表ret作为杨辉三角

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1 
...

2. 第一行只有一个1，比较特殊，要单独处理。定义 list0，并添加1，接着ret添加list0，作为第一行
3. 第二行以后就可以用循环实现。外层循环从i=1开始，到指定行数截止。
4. 定义列表curRow，先添加1，再调用循环添加中间数据。
5. 定义列表prevRow，用来获取上一行的元素。当前行第j个数据就是上一行第j-1与第j个数据之和。循环从1开始，到i结束。最后在尾部添加1，并把curRow加到ret中

代码示例

public class Solution1 {public List<List<Integer>> generate(int numRows) {List<List<Integer>> ret = new ArrayList<>();List<Integer> list0 = new ArrayList<>();list0.add(1);ret.add(list0);for(int i = 1 ; i<numRows;i++){List<Integer> curRow = new ArrayList<>();//头部curRow.add(1);//中间List<Integer> prevRow = ret.get(i-1);for(int j = 1;j<i;j++){curRow.add(prevRow.get(j-1)+prevRow.get(j));}//尾部curRow.add(1);ret.add(curRow);}return ret;}
}

旋转数组

题目描述

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

解题思路

思路1： 当k大于数组长度时，只需要取余。令k=k % nums.length，创建变量tmp存放nums[0],再依次向左挪动元素，把tmp赋给最后一个空间，循环k次。这种解法虽然正确，但是时间花销太大，力扣不予通过。

思路2：先整体翻转，再分两次翻转回来

1. 定义一个方法翻转数组
2. 先整体翻转
3. 把下标k-1之前的元素翻转回来
4. 把下标k以后的元素翻转回来

代码示例

class Solution2 {void rotate(int[] nums, int left, int right){while(left < right){int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}}public void rotate(int[] nums, int k) {k %= nums.length;rotate(nums, 0, nums.length-1);//7 6 5 4 3 2 1 rotate(nums, 0, k-1);//5 6 7 4 3 2 1rotate(nums, k, nums.length-1);// 5 6 7 1 2 3 4 }
}

洗牌算法

1. 功能描述：

1. 生成一副牌（52张）
2. 打乱顺序
3. 分发给三个人，每次发五张

2. 代码设计

• Card类：封装一张扑克牌的属性（花色+点数），是数据载体；
• CardDemo类：包含创建牌组、洗牌、发牌的核心方法，是行为实现的工具类。

3. 核心功能

（1） 定义扑克牌实体（Card类）

一张牌包含花色和点数两个属性，同时需要重写toString()方法，直观表示这两个属性。

public class Card {//花色（♥️、♠️、♣️、♦️）、点数（1-13，对应A-K）private String suit;private int rank;public Card(String suit, int rank) {this.suit = suit;this.rank = rank;}@Overridepublic String toString() {// 将1转为A，11转为J，12转为Q，13转为KString rankStr = switch (rank) {case 1 -> "A";case 11 -> "J";case 12 -> "Q";case 13 -> "K";default -> String.valueOf(rank);};return suit + rankStr;}public String getSuit() {return suit;}public int getRank() {return rank;}
}

关键说明：

• rank（点数）用1-13表示，后续通过toString()转为更易读的“A、2-10、J、Q、K”；
• 必须重写toString()，否则调用cardList.toString()时，会输出[Card.Card@1b6d3586, ...]这类对象地址，无法看到实际牌面。

（2） 创建完整牌组（buyCards()方法）

static final String[] suits = {"♥️", "♠️", "♣️", "♦️"};public List<Card> buyCards() {List<Card> cardList = new ArrayList<>();// 遍历点数（1-13，对应A-K）for (int i = 1; i <= 13; i++) {// 遍历花色for (int j = 0; j < 4; j++) {Card newCard = new Card(suits[j], i);cardList.add(newCard);}}return cardList;
}

（3）洗牌算法（shuffle()方法）

算法原理：

1. 从牌组的最后一张牌（索引size-1）开始，向前遍历；
2. 对于当前索引i，生成一个[0, i]范围内的随机索引j；
3. 交换索引i和j对应的两张牌；
4. 重复步骤2-3，直到遍历到第2张牌（索引1）。

为什么从后往前？
确保每一张牌被交换到随机位置的概率均等（每一步都有1/(i+1)的概率被选中），避免重复交换导致的随机性偏差。

public void shuffle(List<Card> cardList) {Random random = new Random();for (int i = cardList.size() - 1; i > 0; i--) {// 生成[0, i]范围内的随机索引j（nextInt(i+1)的范围是0到i）int j = random.nextInt(i + 1);swap(cardList, i, j);}
}void swap(List<Card> cardList, int i, int j) {Card tmp = cardList.get(j);cardList.set(j, cardList.get(i));cardList.set(i, tmp);
}

注意： random.nextInt(i + 1)：必须加1，否则nextInt(i)的范围是[0, i-1]，会导致最后一张牌永远不会被交换到第1个位置；

（4）发牌逻辑（play()方法）

发牌的需求是“将洗好的牌分发给3个人，每人5张”，核心思路是“循环发牌，每次给1个人发1张，直到发完15张（3人×5张）”。

public void play(List<Card> cardList) {// 存储3个玩家的牌组，每个玩家是一个List<Card>List<List<Card>> personList = new ArrayList<>(3);List<Card> person1 = new ArrayList<>();List<Card> person2 = new ArrayList<>();List<Card> person3 = new ArrayList<>();personList.add(person1);personList.add(person2);personList.add(person3);for (int i = 0; i < 5; i++) {for (int j = 0; j < 3; j++) {Card card = cardList.removeFirst();personList.get(j).add(card);}}

4. 测试

public static void main(String[] args) {CardDemo cardDemo = new CardDemo();// 买牌List<Card> cardList = cardDemo.buyCards();System.out.println("买牌后（未洗牌）：" + cardList);// 洗牌cardDemo.shuffle(cardList);System.out.println("\n洗牌后：" + cardList);// 发牌System.out.println("\n发牌结果：");cardDemo.play(cardList);// 剩余牌组System.out.println("\n剩余牌数：" + cardList.size() + "张");System.out.println("剩余牌组：" + cardList);
}

测试结果：

买牌后：[♥️A, ♠️A, ♣️A, ♦️A, ♥️2, ♠️2, ..., ♦️K]洗牌后：[♣️5, ♥️J, ♦️7, ♠️3, ♣️Q, ..., ♥️8]发牌结果：
玩家1的牌：[♣️5, ♦️3, ♠️J, ♣️7, ♦️Q]
玩家2的牌：[♥️J, ♥️5, ♦️K, ♠️8, ♣️2]
玩家3的牌：[♦️7, ♠️A, ♣️K, ♥️9, ♦️2]剩余牌数：37张
剩余牌组：[♠️10, ♥️3, ..., ♥️8]