将 x 减到 0 的最小操作数

目录

一：题目链接

二：题目思路

        方法一：

方法二：

三：代码实现

---

一：题目链接

        题目理解需要注意的是，数字 x 只能减去数组最左边或者最右边的元素，并且减去的数组元素在数组不能再重复使用，比如数字 x 减去 left 位置的元素后，后续只能使用 left + 1位置的元素或者 right 位置的元素（right 位置同理）。如下图：

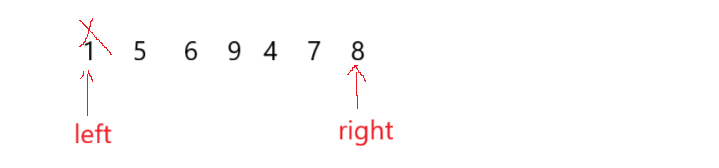
二：题目思路

        正着理解题目做题有点不好做，我们可以把题目要求反着来理解：

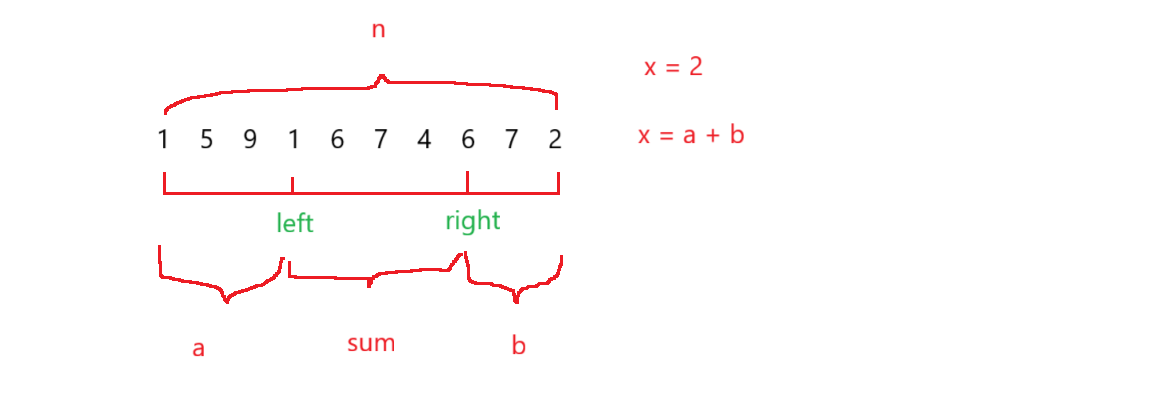
        如上图，n 是数组总和， a 和 b 和 sum 代表其各自位置子数组的和。题目要求也就变成了，在数组 left 和 right 区间找到最长的子数组，使得 sum  = n - x。

方法一：

        现在，我们可以使用暴力枚举区间的方法来大致实现了，定义指针 left 和 right 在数组起始位置，left 先固定，right 不断往后在走，期间 sum 不断记录当前 right 和 left 区间的总和，当 sum = n - x 后，记录当前 right 和 left 之间的子数组长度，当 sum > n - x 后; left ++，right 回到 left 位置 继续往后走，重复上述过程，直到 left 到数组末尾，返回总的过程符合 sum = n - x 条件最大的子数组长度。

        现在，我们可以对上述算法优化一下。

方法二：

   

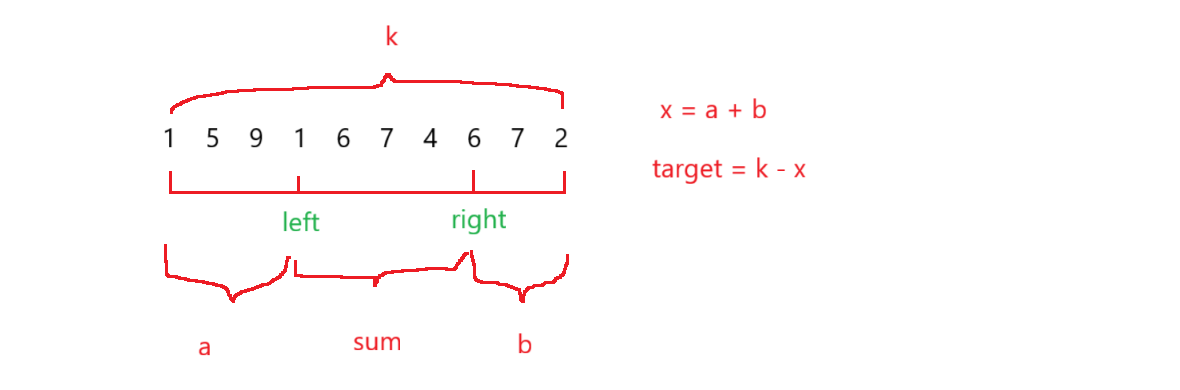
        上面的是过程图。首先，定义子数组要求的和 target ，定义指针 left 和 right 在数组起始位置，left 先固定，right 不断往后在走，期间 sum 不断记录当前 right 和 left 区间的总和，当 sum = target 后，记录当前 right 和 left 之间的子数组长度，当 sum > target 后，sum 减去当前nums[left] 的值，left ++ ，直到 sum <= target ，right 就可以继续往后走。重复上述过程，直到 right 到达数组末尾结束。返回总的过程记录的多个 right 和 left 之间的子数组长度中最大的值。

        

三：代码实现

        //记录子数组最长的长度int len = -1;//记录当前子数组的和int sum = 0;int n = nums.length;//数组总的和int k = 0;for(int i = 0;i < n;i++) {k += nums[i];}//子数组要求的和int target = k - x;//细节处理（如果 x 比数组总和大，就直接返回 -1 ）if(target < 0) {return -1;}int left = 0;for(int right = 0;right < n;right++) {//进窗口sum += nums[right];while(sum > target) {sum -= nums[left];left++;}//记录当前符合条件子数组的长度if(sum == target) {len = Math.max(len,right - left + 1);}}if(len == -1) {return -1;}return n - len;