基于联邦学习与神经架构搜索的可泛化重建:用于加速磁共振成像|文献速递-最新医学人工智能文献
Title
题目
Generalizable Reconstruction for AcceleratingMR Imaging via Federated Learning WithNeural Architecture Search
基于联邦学习与神经架构搜索的可泛化重建:用于加速磁共振成像
01
文献速递介绍
磁共振成像(MRI)是一种无创成像方式,能够有效评估软组织的结构、形态与功能。因其可提供详细且全面的信息,MRI在临床诊断与疾病评估中发挥着关键作用。然而,受扫描设备物理局限性的影响[1],获取全采样k空间数据通常十分耗时。提升成像速度的一种可行方法是从欠采样数据中重建高质量图像[2]。近年来,深度学习在加速磁共振图像重建方面展现出巨大潜力[3]-[18]。通过从大规模数据集离线学习,深度学习具备在线快速重建的优势[3]。但由于扫描设备不同、成像协议差异等因素,不同中心的数据分布可能存在显著异质性[19]。这导致在一个中心训练的模型难以推广到其他中心,同时也难以保证模型性能的稳定性,进而可能造成模型在不同中心的性能存在偏差。 传统解决方法之一是聚合多中心数据进行集中式学习[20]。但收集多中心数据不仅会消耗大量资源,还可能导致患者隐私泄露[21]-[22]。 为解决这一局限,联邦学习应运而生,成为一种极具潜力的框架——它可支持多机构协同学习,同时保护患者隐私[19]、[23]-[33]。在联邦学习中,每个客户端利用自身计算资源和私有数据独立训练本地模型;随后,服务器收集所有客户端训练的本地模型,并采用聚合方法得到服务器模型;最后,服务器将聚合后的模型分发给各客户端,用于后续通信轮次[24]。经典联邦学习方法FedAvg[24]在客户端模型数据分布一致时,聚合效果良好。但在磁共振成像场景中,不同组织对比度、成像协议等因素会导致不同客户端的数据分布存在异质性,这可能使联邦学习训练的模型性能下降。已有研究提出多种联邦学习磁共振成像方法以缓解该问题:文献[29]通过反复对齐源站点与目标站点的 latent 空间表示,提升其相似性;文献[19]将重建模型分为全局共享编码器与本地个性化解码器,以保留客户端特异性。尽管现有联邦学习磁共振图像重建方法已取得较好性能,但这些方法的重建模型通常采用专家手动设计的网络架构,结构复杂且需消耗大量计算资源。此外,这些方法也极少考虑算法公平性问题——在数据分布异质的情况下,模型在不同中心的性能往往存在明显差距,这使得训练后的模型难以推广到其他中心[31]。 神经架构搜索(NAS)[34]可自动搜索最优网络架构,在提升模型性能的同时降低计算资源消耗。典型的NAS架构包含搜索空间、搜索方法与评估方法三部分。近年来,已有部分研究将NAS单独应用于磁共振图像重建[35]-[36],这些方法均取得了改进效果:与现有手动设计模型相比,在模型参数更少的情况下实现了更优性能。但这些方法并未考虑不同中心的数据分布异质性问题。 针对上述挑战,本文提出一种用于加速磁共振成像的可泛化联邦神经架构搜索框架。主要贡献总结如下: 1)提出可泛化联邦神经架构搜索框架(GAutoMRI),该框架以保护隐私的方式利用多机构数据,实现欠采样磁共振图像的精准重建,且模型具备轻量化特性。 2)设计公平性调整方法,提升模型在不同中心的学习能力,使模型对分布内数据与分布外数据均能实现更优泛化。 3)在三个公开数据集与一个内部数据集上开展大量实验验证,这些数据集具有不同的欠采样模式、成像方式与扫描设备。结果表明,与七种最先进的联邦学习方法相比,本文提出的GAutoMRI不仅性能更优、泛化能力更强,且模型轻量化程度显著提升。
Aastract
摘要
Heterogeneous data captured by differentscanning devices and imaging protocols can affect thegeneralization performance of the deep learning magneticresonance (MR) reconstruction model. While a centralized training model is effective in mitigating this problem,it raises concerns about privacy protection. Federatedlearning is a distributed training paradigm that can utilizemulti-institutional data for collaborative training withoutsharing data. However, existing federated learning MRimage reconstruction methods rely on models designedmanually by experts, which are complex and computationally expensive, suffering from performance degradationwhen facing heterogeneous data distributions. In addition,these methods give inadequate consideration to fairnessissues, namely ensuring that the model’s training does notintroduce bias towards any specific dataset’s distribution.To this end, this paper proposes a generalizable federatedneural architecture search framework for accelerating MRimaging (GAutoMRI). Specifically, automatic neural architecture search is investigated for effective and efficientneural network representation learning of MR images fromdifferent centers. Furthermore, we design a fairness adjustment approach that can enable the model to learn featuresfairly from inconsistent distributions of different devicesand centers, and thus facilitate the model to generalize wellto the unseen center. Extensive experiments show that ourproposed GAutoMRI has better performances and generalization ability compared with seven state-of-the-art federated learning methods. Moreover, the GAutoMRI model issignificantly more lightweight, making it an efficient choicefor MR image reconstruction tasks.
不同扫描设备和成像协议捕获的异质数据,会影响深度学习磁共振(MR)重建模型的泛化性能。尽管集中式训练模型能有效缓解这一问题,但它引发了隐私保护方面的担忧。联邦学习是一种分布式训练范式,可利用多机构数据进行协同训练,且无需共享数据。然而,现有联邦学习磁共振图像重建方法依赖专家手动设计模型,这类模型结构复杂、计算成本高,在面对异质数据分布时会出现性能下降。此外,这些方法对公平性问题考虑不足,即未能确保模型训练不会对任何特定数据集的分布产生偏向性。 为此,本文提出一种用于加速磁共振成像的可泛化联邦神经架构搜索框架(GAutoMRI)。具体而言,本文研究了自动神经架构搜索技术,以实现对来自不同中心磁共振图像的高效且有效的神经网络表示学习。此外,本文设计了一种公平性调整方法,该方法能使模型从不同设备和中心的不一致分布中公平地学习特征,进而助力模型对未见过的中心数据实现良好泛化。大量实验表明,与七种最先进的联邦学习方法相比,本文提出的GAutoMRI具有更优的性能和泛化能力。此外,GAutoMRI模型的轻量化程度显著更高,使其成为磁共振图像重建任务的高效选择。
Method
方法
A. DL-Based MR Image Reconstruction
The goal of MR image reconstruction is to reconstruct ahigh-quality image x ∈ C N (M < N) from undersampledk-space data b ∈ C M , formulated as:b** = Ax + ϵ, (1)where A ∈ C M×N denotes the encoding matrix and ϵ ∈ C Mdenotes the measurement noise. Solving x from Eq. (1) isan ill-posed inverse problem that can be expressed as thefollowing optimization problem:minx12∥Ax − b∥ + λR(x), (2)where the first term is the data fidelity, the second term is theregularization term, and λ is the regularization parameter usedto balance the tradeoff between the data fidelity term and theregularization term. Based on the method of model unfolding[8], Eq. (2) can be transformed into the following alternatingiteration process:z j = fθ x j**xj+1 = A H A + λI −1 A H b + λzj ,(3)where fθ denotes the deep neural network used for denoising,AH* denotes the conjugate operator of A, j denotes the iterativecontrol variable, and λ is learnable.
A. 基于深度学习的磁共振图像重建 磁共振(MR)图像重建的目标是从欠采样k空间数据b ∈ C^M中重建出高质量图像x ∈ C^N(其中M < N),其数学表达式为: b = Ax + ϵ (1) 式中,A ∈ C^(M×N)表示编码矩阵,ϵ ∈ C^M表示测量噪声。从式(1)中求解x是一个不适定逆问题,可转化为如下优化问题: minₓ (1/2)∥Ax − b∥ + λR(x) (2) 其中,第一项为数据保真项,第二项为正则化项,λ为正则化参数,用于平衡数据保真项与正则化项之间的权衡关系。基于模型展开方法[8],可将式(2)转化为以下交替迭代过程: $\begin{cases} \mathbf{z}^j = f{\theta}(\mathbf{x}^j) \ \mathbf{x}^{j+1} = \left( \mathbf{A}^H \mathbf{A} + \lambda \mathbf{I} \right)^{-1} \left( \mathbf{A}^H \mathbf{b} + \lambda \mathbf{z}^j \right) \end{cases}$ (3) 式中,$f{\theta}$表示用于去噪的深度神经网络,$\mathbf{A}^H$表示A的共轭算子,j表示迭代控制变量,且λ为可学习参数。
Conclusion
结论
In this paper, we focus on addressing the generalizationissue of deep learning MR image reconstruction modelstowards heterogeneous data captured by different scanningdevices and imaging protocols, using multi-institutional datain a privacy-preserving manner. Specifically, we propose ageneralizable federated neural architecture search framework,GAutoMRI. In the framework, we first design a new searchspace tailored for the undersampled MR image reconstruction task. Then, we use a differentiable federated neuralarchitecture search method to learn an optimal model fromheterogeneous data distributions. In addition, we design afairness adjustment approach that can enable the model tolearn features fairly from inconsistent distributions of differentdevices. Extensive experiments on different sampling patterns,acceleration rates, contrasts, and unseen centers demonstratethat our proposed GAutoMRI has better generalization andperformance compared to seven state-of-the-art federatedlearning methods.
本文旨在以保护隐私的方式利用多机构数据,解决深度学习磁共振(MR)图像重建模型针对不同扫描设备与成像协议所捕获异质数据的泛化问题。具体而言,本文提出一种可泛化联邦神经架构搜索框架(GAutoMRI)。在该框架中,首先针对欠采样磁共振图像重建任务设计了一个新的搜索空间;随后,采用可微分联邦神经架构搜索方法,从异质数据分布中学习得到最优模型;此外,本文还设计了一种公平性调整方法,该方法能使模型从不同设备的不一致数据分布中公平地学习特征。在不同采样模式、加速率、对比度及未见过的中心数据上开展的大量实验表明,与七种最先进的联邦学习方法相比,本文提出的GAutoMRI具有更优的泛化能力与性能。 参考文献 (注:原文末尾“REFERENCES”为参考文献标识,此处保留该标识,后续通常会列出具体参考文献条目,如期刊论文、会议论文、专著等,格式一般遵循学术规范,包含作者、标题、发表刊物/会议、年份、卷期、页码或DOI等信息。)
Figure
图
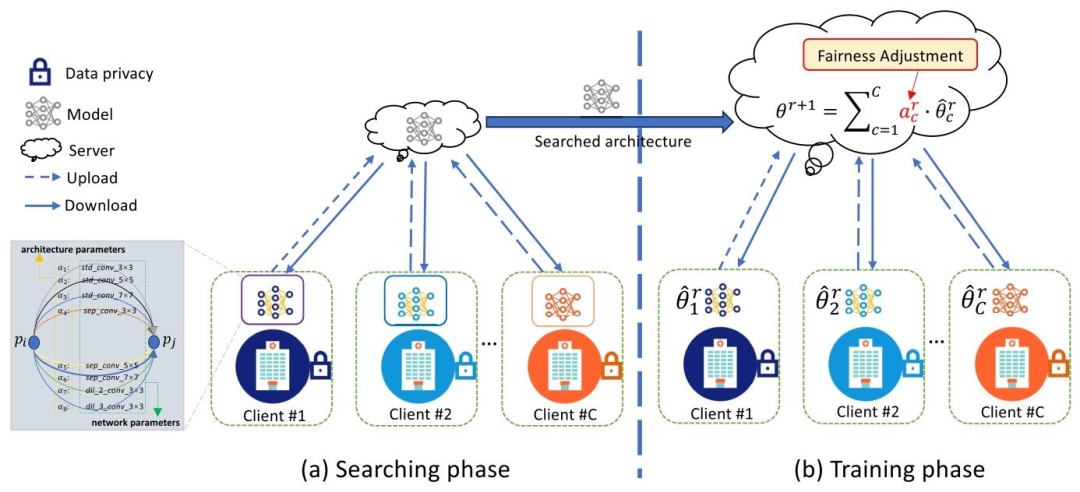
Fig. 1. The overall architecture of our proposed GAutoMRI. It consists of two phases: (a) Searching phase. This phase aims to obtain the optimalarchitecture using the federated neural architecture search method and use the searched architecture for the training phase. (b) Training phase.The optimal architecture obtained in the searching phase is utilized as the base model. In addition, we introduce a fairness adjustment approach toimprove the generalization of the global model over out-of-distribution data, as detailed in III.C.
图1 本文提出的GAutoMRI整体架构 该架构包含两个阶段:(a)搜索阶段。此阶段旨在通过联邦神经架构搜索方法获取最优架构,并将搜索得到的架构用于训练阶段。(b)训练阶段。将搜索阶段得到的最优架构作为基础模型,此外,本文引入公平性调整方法以提升全局模型对分布外数据的泛化能力,详见第III.C节。
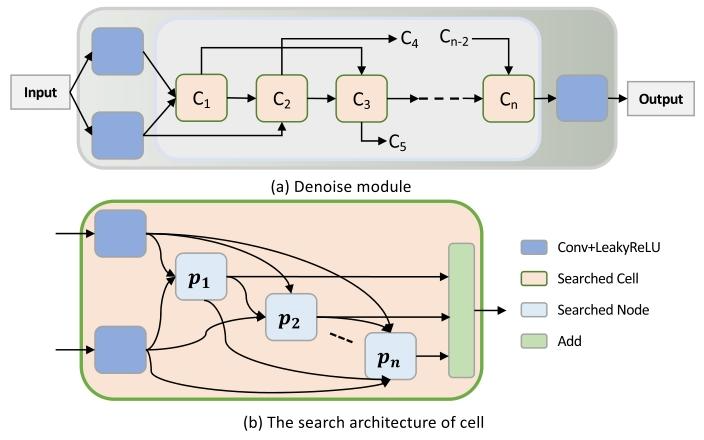
Fig. 2. The overall structure of the search space. (a) The structure ofdenoiser module fθ (·) in our reconstruction network. The searched cellsare stacked to form our basic architecture, with each cell connected tothe two consecutive cells that follow it. (b) The search architecture of thecell. pn denotes the node in the cell.
图2 搜索空间的整体结构 (a)重建网络中去噪器模块$f_\theta(·)$的结构。通过搜索得到的单元(cell)堆叠形成基础架构,每个单元均与其后续的两个连续单元相连。(b)单元的搜索架构。$p_n$表示单元中的节点。
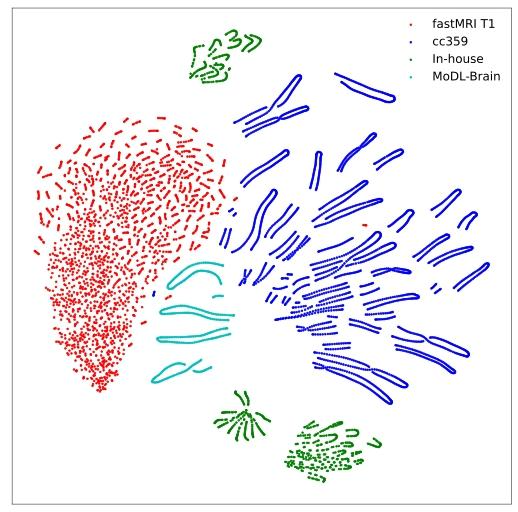
Fig. 3. T-SNE visualization of data distributions from four clients: fastMRIT1, cc359, In-house, and MoDL-Brain.
图3 四个客户端数据分布的T-SNE可视化结果 这四个客户端分别为fastMRI T1、cc359、内部数据集(In-house)和MoDL-Brain。

Fig. 4. The network architecture obtained during the searching phase.
图4 搜索阶段得到的网络架构
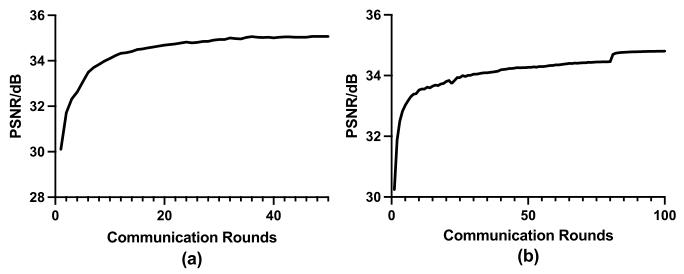
Fig. 5. Evaluation metric charts corresponding to the searching phaseand training phase. (a) Searching phase. (b) Training phase.
图5 搜索阶段与训练阶段对应的评估指标图 (a)搜索阶段对应的评估指标图;(b)训练阶段对应的评估指标图。
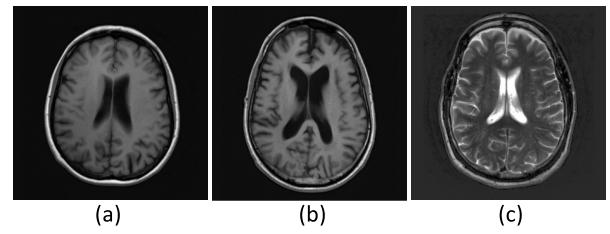
Fig. 6. Contrast visualization examples of in-distribution and out-ofdistribution data. (a) and (b): T1-weighted image; (c): T2-weighted image.
图6 分布内数据与分布外数据的对比可视化示例 (a)、(b)为T1加权图像;(c)为T2加权图像。
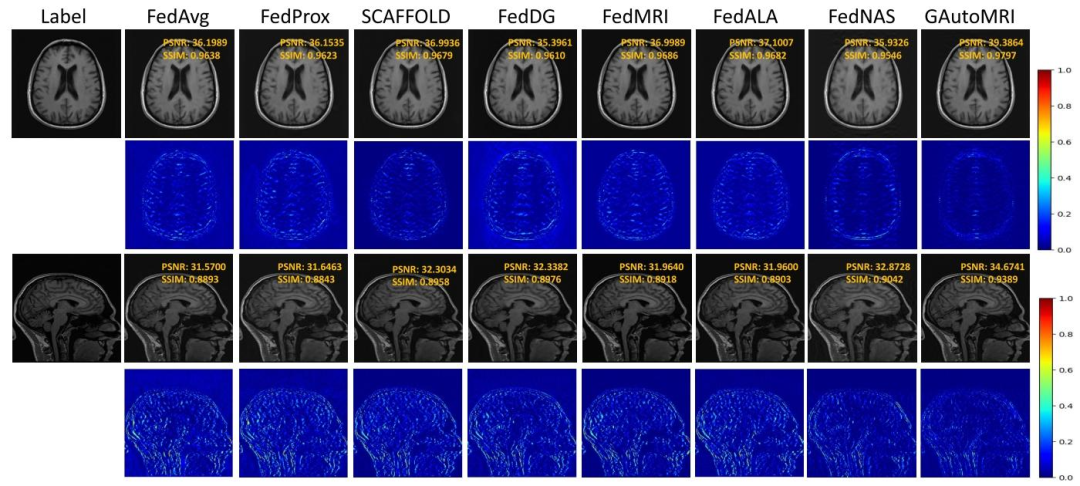
Fig. 7. Qualitative reconstruction results of different methods under the in-distribution scenario. From left to right column: The reference image, theresults of FedAvg, FedProx, SCAFFOLD, FedDG, FedMRI, FedALA, FedNAS, and GAutoMRI, respectively. The second and fourth rows plot thecorresponding error maps.
图7 分布内场景下不同方法的定性重建结果 从左至右各列依次为:参考图像、FedAvg方法结果、FedProx方法结果、SCAFFOLD方法结果、FedDG方法结果、FedMRI方法结果、FedALA方法结果、GAutoMRI方法结果。其中,第二行与第四行展示了对应的误差图。
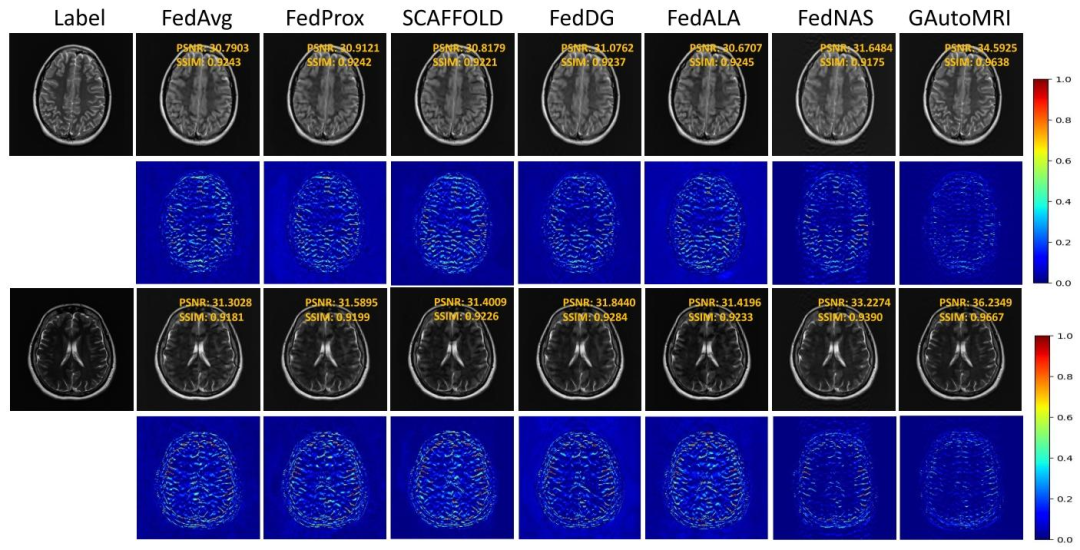
Fig. 8. Qualitative reconstruction results of different methods under the out-of-distribution scenario 3. From left to right column: The referenceimage, the results of FedAvg, FedProx, SCAFFOLD, FedDG, FedALA, FedNAS, and GAutoMRI, respectively. The second and fourth rows plot thecorresponding error maps
图8 分布外场景3下不同方法的定性重建结果 从左至右各列依次为:参考图像、FedAvg方法结果、FedProx方法结果、SCAFFOLD方法结果、FedDG方法结果、FedALA方法结果、FedNAS方法结果、GAutoMRI方法结果。其中,第二行与第四行展示了对应的误差图。
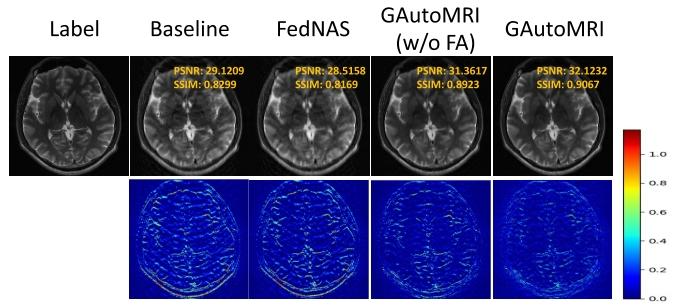
Fig. 9. Qualitative results of ablation experiment under the in-distributionscenario. (w/o FA) indicates without fairness adjustment method.
图9 分布内场景下消融实验的定性结果 (w/o FA)表示“未采用公平性调整方法”(where "w/o FA" stands for "without fairness adjustment method")。
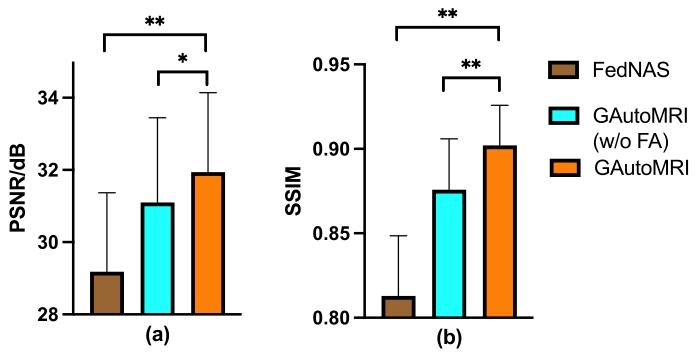
Fig. 10. Quantitative results of ablation experiment under the out-ofdistribution scenario 4. (w/o FA) indicates without fairness adjustmentmethod. The p-value is described in the figure, where represents p <0.01 and represents p < 0.001.
图10 分布外场景4下消融实验的定量结果 (w/o FA)表示“未采用公平性调整方法”(其中“w/o FA”为“without fairness adjustment method”的缩写)。图中给出了p值,其中代表p<0.01,**代表p*<0.001。
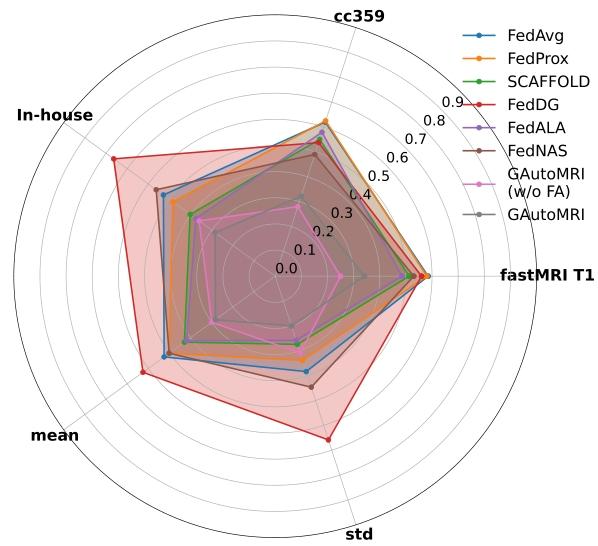
Fig. 11. Radar chart of the testing errors of the global model under thein-distribution scenario. (w/o FA) indicates without fairness adjustmentmethod.
图11 分布内场景下全局模型测试误差的雷达图 (w/o FA)表示“未采用公平性调整方法”(其中“w/o FA”为“without fairness adjustment method”的缩写)。
Table
表
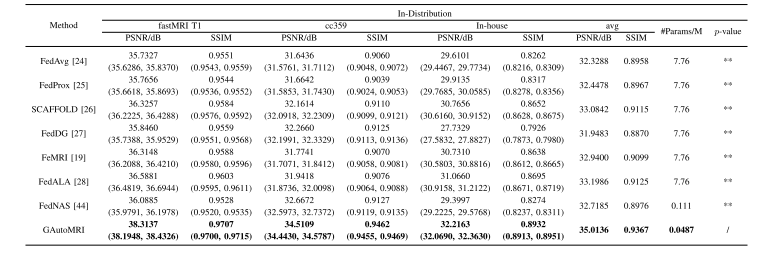
Table i quantitative results of different methods. bold numbers indicate the best results. detailed analyses are described in iv.b. the p-value is described in the table, where represents p < 0.001
表1 不同方法的定量结果 粗体数字表示最佳结果,详细分析见第IV.B节。表中给出了p值,其中代表p<0.001。
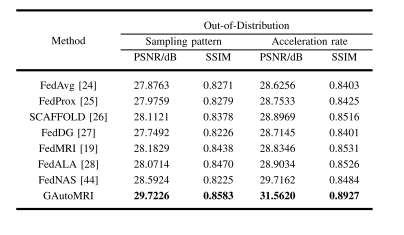
Table ii quantitative results of different methods. bold numbers indicate the best results. detailed analyses are described in iv.c.1
表2 不同方法的定量结果 粗体数字表示最佳结果,详细分析见第IV.C.1节。
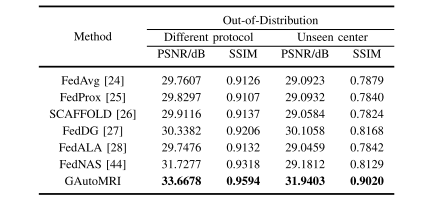
Table iii quantitative results of different methods. bold numbers indicate the best results. detailed analyses are described in iv.c.2
表3 不同方法的定量结果 粗体数字表示最佳结果,详细分析见第IV.C.2节。

Table iv comparison of the number of parameters between the proposed method and baseline model
表4 所提方法与基准模型的参数数量对比
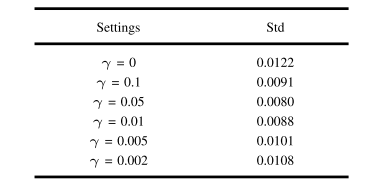
Table v the different standard deviations of the test error of the global model under the in-distribution scenario when γ takes different values
表5 当γ取不同值时,分布内场景下全局模型测试误差的不同标准差
