C++动态规划算法:斐波那契数列模型
本期我们将开启一个C++算法中一个重要的部分:动态规划
动态规划是一个与贪心不同的问题,贪心注重于当下的每一步而达到“全局最优”,而动态规划则注重于整体的全局最优。
本篇我们来介绍一下动态规划算法中一个重要的模型——斐波那契数列模型
相关题目代码已经上传至作者的个人gitee:楼田莉子/C++算法学习喜欢请支持一下,谢谢
目录
动态规划(Dynamic Programming)
核心思想
动态规划步骤
1、状态表示
2、状态转移方程
3、初始化
4、填表顺序
1、第N个泰波那契数
2、三步问题
3、使用最小的花费爬楼梯
4、解码方法
动态规划(Dynamic Programming)
动态规划是一种用于解决复杂问题的算法设计技术,它通过将问题分解为相互重叠的子问题,并存储子问题的解以避免重复计算,从而有效提高计算效率。动态规划通常适用于具有最优子结构(即问题的最优解包含其子问题的最优解)和重叠子问题(即子问题会重复出现)性质的问题。
核心思想
- 分治思想:将原问题分解为若干子问题,递归求解子问题。
- 记忆化存储:存储子问题的解,避免重复计算(通常使用数组或哈希表)。
- 自底向上或自顶向下:
- 自顶向下(Top-Down):递归分解问题,结合记忆化(如斐波那契数列的备忘录方法)。
- 自底向上(Bottom-Up):从最小子问题开始迭代求解,逐步构建更大问题的解(如填表法)。
动态规划步骤
1、状态表示
dp表中表示的含义。
来源:1、题目来源2、经验3、发现重复子
2、状态转移方程
dp[i]=dp[i-1]+……
3、初始化
保证填表的时候不越界
4、填表顺序
为了填写当前状态已经计算过的
1、第N个泰波那契数

算法原理:
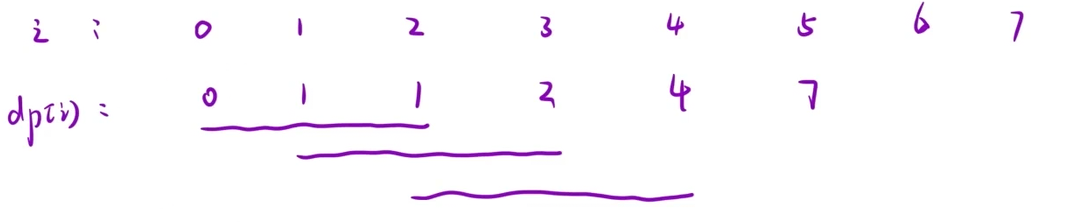
初始化dp[0]=0、dp[1]、dp[2]为1
class Solution {
public:int tribonacci(int n) {//处理边界问题if(n==0) return 0;if(n==1||n==2) return 1;//创建dp表vector<int>dp(n+1);//初始化dp[0]=0,dp[1]=1,dp[2]=1;//填表for(int i=3;i<=n;i++)dp[i]=dp[i-1]+dp[i-2]+dp[i-3];//返回值return dp[n];}
};优化:背包问题
滚动数组
class Solution {
public:int tribonacci(int n) {//优化前// //处理边界问题// if(n==0) return 0;// if(n==1||n==2) return 1;// //创建dp表// vector<int>dp(n+1);// //初始化// dp[0]=0,dp[1]=1,dp[2]=1;// //填表// for(int i=3;i<=n;i++)// dp[i]=dp[i-1]+dp[i-2]+dp[i-3];// //返回值// return dp[n];//优化后if(n==0) return 0;if(n==1||n==2) return 1;int a=0,b=1,c=1,d=0;for(int i=3;i<=n;i++){d=a+b+c;a=b;b=c;c=d;} return d;}
};2、三步问题

算法思想:
dp[i]:到i位置有多少种方法
从[i-1]到[i],为dp[i-1]
从[i-2]到[i],为dp[i-2]
从[i-3]到[i],为dp[i-3]
dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
dp[1]=1,dp[2]=2,dp[3]=4
class Solution {
public:int waysToStep(int n) {const int MOD=1e9+7;//边界调节处理// if(n==1||n==2) return n;// if(n==3) return 4;// vector<int>dp(n+1);// dp[1]=1,dp[2]=2,dp[3]=4;// for(int i=4;i<=n;i++)// //每次加法都要取模// dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;// return dp[n];//优化后if(n==1||n==2) return n;if(n==3) return 4;int a=1,b=2,c=4,d=0;for(int i=4;i<=n;i++){d=((a+b)%MOD+c)%MOD;a=b;b=c;c=d;} return d;}
};3、使用最小的花费爬楼梯

算法思想:
算法一:
dp[i]:到达i位置的最小花费
先到达i-1位置,支付cost[i-1]走一步
先到达i-1位置,支付cost[i-2]走两步
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
算法二:
dp[i]:从i位置触发到达终点的最小花费
dp[i]:
支付cost[i],向后一步,从i+1位置出发
支付cost[i],向后两步,从i+2位置出发
dp[i-1]=cost[i-1];dp[i-2]=cost[i-2]
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//算法一:// int n=cost.size();// vector<int>dp(n+1);// dp[0]=0,dp[1]=0; // for(int i=2;i<=n;i++)// dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);// return dp[n];//算法二:int n=cost.size();vector<int>dp(n+1);dp[n-1]=cost[n-1];dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--)dp[i]=cost[i]+min(dp[i+1],dp[i+2]);return min(dp[0],dp[1]);}
};4、解码方法


算法思想:
以i为结尾,dp[i]表示以i为结尾的时候解码的总数。
dp[i]:

dp[i]=dp[i-1]+dp[i-2]
细节问题:边界情况的处理
1、虚拟节点的值保证后面的填表正确
2、下标的映射关系正确
class Solution {
public:int numDecodings(string s) {//算法一// int n=s.size();// vector<int>dp(n);// dp[0]=s[0]!='0';// //处理特殊情况// if(n==1) return dp[0];// if(s[0]!='0'&&s[1]!='0') dp[1]+=1;// int t=(s[0]-'0')*10+s[1]-'0';//前两个位置表示的数// if(t>=10&&t<=26) dp[1]+=1;// for(int i=2;i<n;i++)// {// if(s[i]!='0') dp[i]+=dp[i-1];//处理单独编码的情况// int t=(s[i-1]-'0')*10+s[i]-'0';//第二种情况对应的数// if(t>=10&&t<=26) dp[i]+=dp[i-2];// }// return dp[n-1];//算法二int n=s.size();vector<int>dp(n+1);dp[0]=1;//s[1-1]dp[1]=s[0]!='0';for(int i=2;i<=n;i++){if(s[i-1]!='0') dp[i]+=dp[i-1];//处理单独编码的情况int t=(s[i-2]-'0')*10+s[i-1]-'0';//第二种情况对应的数if(t>=10&&t<=26) dp[i]+=dp[i-2];}return dp[n];}
};本期动态规划第一个模型的内容就到这里了,喜欢请点个赞支持一下谢谢
