变分自编码器详解与实现

0. 前言

在自编码器中，解码器直接从潜变量中采样。 变分自编码器 (Variational Autoencoder, VAE) 的不同之处在于，采样是从由潜变量参数化的分布中获取的。为了清楚起见，假设我们有一个带有两个潜变量的自编码器，我们随机抽取样本并得到两个样本，然后，我们将它们发送到解码器以生成图像。
在 VAE 中，这些样本不会直接进入解码器。取而代之的是，它们被用作高斯分布的均值和方差，并且我们从该分布中提取样本发送给解码器以进行图像生成。由于高斯分布是机器学习中最重要的分布之一，因此在创建 VAE 之前，我们先介绍高斯分布的一些基础知识。

1. 高斯分布

高斯分布的特征在于两个参数-均值和方差：

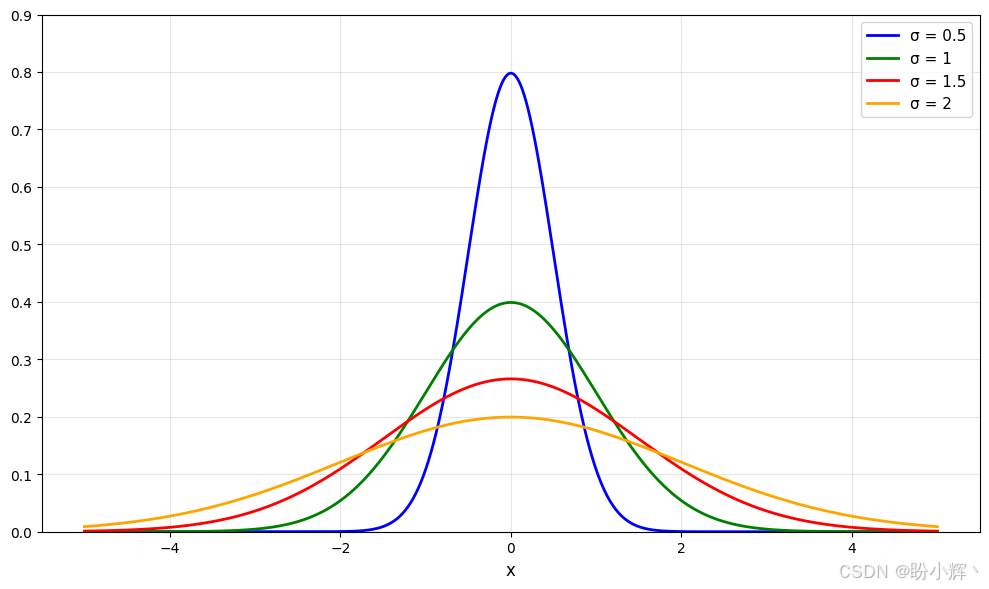
我们可以使用 $N(\mu ,{\sigma }^2)$ 表示法来描述单变量高斯分布，其中 $\mu$ 是平均值，$\sigma$ 是标准差。
平均值是具有最高概率密度的值，换句话说，就是频率最高的值。如果我们要绘制图像的像素位置 $(x,y)$ 的样本，并且每个 $x$ 和 $y$ 具有不同的高斯分布，则为多元高斯分布。在这种情况下，它是一个双变量分布。
我们将标准差合并到协方差矩阵中。协方差矩阵中的对角元素是各个高斯分布的标准偏差。其他元素测量两个高斯分布之间的协方差，即它们之间的相关性。
下图展示了无相关性的双变量高斯分布样本：

可以看到，当一个维度的标准差从 1 增加到 4 时，散布仅在那个维度 (y 轴)上增加而对其他维度没有影响。在这里，我们说两个高斯分布是独立同分布的 (identically and independently distributed, iid)。
在以下示例中，左侧的图显示协方差非零且为正，这意味着当密度在一个维度上增加时，另一维度将随之变化并将它们相关联。右图显示负相关：

假设 VAE 中的高斯分布是 iid，因此不需要协方差矩阵来描述变量之间的相关性。我们只需要 n 对均值和方差即可描述多元高斯分布。我们希望实现的目标是创建一个分布良好的潜空间，其中不同数据类的潜变量分布如下：

• 均匀分布，因此我们可以从中进行更好的采样
• 彼此稍微重叠以形成连续的过渡

接下来，我们将学习如何将高斯分布采样合并到 VAE 中。

2. 采样潜变量

当我们训练自编码器时，编码后的潜变量直接进入解码器。对于 VAE，在编码器和解码器之间还有一个额外的采样步骤。编码器将高斯分布的均值和方差作为潜变量生成，然后从中提取样本以发送给解码器。问题是，采样不可向后传播，因此不可训练。
为了解决这个问题，我们可以采用一个简单的重参数化技巧，将高斯随机变量 N(mean, variance) 转换为 mean + sigma * N(0, 1)。换句话说，我们首先从标准的高斯分布 $N(0,1)$ 进行采样，然后将其乘以 sigma，然后加上 mean。如下图所示，采样变为仿射变换(仅由加法和乘法运算组成)，并且误差可以从输出反向传播回编码器：

来自标准高斯分布 $N(0,1)$ 的采样可以看作是 VAE 的输入，我们不需要反向传播回输入。但是，我们将 $N(0,1)$ 采样放入模型中。现在我们了解了采样的工作原理，接下来构建 VAE 模型。
将采样实现为自定义层：

class GaussianSampling(Layer):        def call(self, inputs):means, logvar = inputsepsilon=tf.random.normal(shape=tf.shape(means),mean=0., stddev=1.)samples = means + tf.exp(0.5*logvar)*epsilonreturn samples

需要注意的是，我们在编码器空间中使用对数方差，而不是使用数值方差。根据定义，方差是一个正数，但是除非我们使用诸如 relu 之类的激活函数来约束它，否则潜变量的方差可能变为负数。此外，方差可以具有很大地变化范围，例如从 0.01 到 100，这可能会使训练变得困难。但是，这些值的自然对数在一个较小的范围内。不过，在进行采样时，我们需要将对数方差转换为标准差，因此需要使用 tf.exp(0.5 * logvar)。

在TensorFlow 中有多种构造模型的方法。一种是使用 Sequential 类按顺序添加层。最后一层的输入进入下一层；因此，无需指定层的输入。尽管这很方便，但是不能在具有分支的模型上使用它。另一种是使用 Functional API，从输入开始，链接各层，然后为每个层指定输入。但是，tf.random.normal() 在 eager 执行模式下将失败，这是因为函数需要知道 batch 大小才能生成随机数，但是在创建网络层时未知。因此，当尝试通过传入 (None, 2) 来绘制样本时，会出现错误。因此，我们将使用子类化 (subclassing) 完成模型创建，在 call() 运行时，我们将已经知道batch大小，从而获取形状信息。

接下来，我们使用子类化方法重建编码器。如果需要使用输入形状来构造网络层，则可以在 __init __() 或 __built __() 中创建网络层。在子类中，我们可以使用 Sequential 类方便地创建一个卷积层块，因为我们不需要读取任何中间张量：

class Encoder(Layer):def __init__(self, z_dim, name='encoder'):super(Encoder, self).__init__(name=name)        self.features_extract = Sequential([Conv2D(filters=8,  kernel_size=(3,3), strides=2, padding='same', activation='relu'),Conv2D(filters=8,  kernel_size=(3,3), strides=1, padding='same', activation='relu'),Conv2D(filters=8,  kernel_size=(3,3), strides=2, padding='same', activation='relu'),Conv2D(filters=8,  kernel_size=(3,3), strides=1, padding='same', activation='relu'),Flatten()])self.dense_mean = Dense(z_dim, name='mean')self.dense_logvar = Dense(z_dim, name='logvar')self.sampler = GaussianSampling()

然后，我们使用两个全连接层从提取的特征中预测 z 的均值和对数方差。对潜变量进行采样，并将其与平均值和对数方差一起作为输出返回，以进行损失计算：

    def call(self, inputs):x = self.features_extract(inputs)mean = self.dense_mean(x)logvar = self.dense_logvar(x)z = self.sampler([mean, logvar])return z, mean, logvar

3. 损失函数

我们现在可以从多元高斯分布中取样，但是仍然不能保证高斯采样点不会彼此相距很远且不会广泛散布。VAE 改变这种情况的方法是通过引入一些正则化来鼓励高斯分布近似 $N(0,1)$。换句话说，我们希望它们的均值接近于 0，以使它们彼此靠得很近；方差接近于 1，以便从中采样更好的变量。这是通过使用 Kullback-Leibler 散度 (Kullback- Leibler divergence, KLD) 完成的。
KLD 用于度量一种概率分布与另一种概率分布的差异。对于 $P$ 和 $Q$ 这两个分布，$P$ 相对于 $Q$ 的 KLD 是 $P$ 和 $Q$ 的交叉熵减去 $P$ 的熵。在信息论中，熵是信息的度量或随机变量的不确定性：
$$D_{KL}(P||Q)=H(P,Q)-H(P)$$
KLD 与交叉熵成正比，因此最小化交叉熵也将最小化 KLD。当 KLD 为零时，两个分布相同。可以说，当要比较的分布是标准高斯分布时，对于 KLD 就有一个闭式解。可以直接从以下均值和方差计算得出：
$$D_{KL}(N(\mu ,\sigma )||N(0,1))=-0.5\sum _{i=1}^{z}log({\sigma }_i^2)-{\sigma }_i^2-{\mu }_i^2+1$$
创建自定义损失函数，该函数接受标签和网络输出以计算 KL 损失。使用 tf.reduce_mean() 将其归一化为潜空间维度的数量：

def vae_kl_loss(y_true, y_pred):kl_loss =  - 0.5 * tf.reduce_mean(vae.logvar - tf.exp(vae.logvar) - tf.square(vae.mean) + 1)return kl_loss

另一个损失函数是我们在自编码器中使用的函数，用于将生成的图像与标签图像进行比较，也称为重建损失，它测量重建图像与目标图像之间的差异。损失可以是二进制交叉熵 (binary cross-entropy, BCE) 或均方误差 (mean squared error, MSE)。MSE 往往会生成更清晰的图像，因为它会对偏离标签的像素进行更严厉的惩罚(通过将误差平方)：

def vae_rc_loss(y_true, y_pred):rc_loss = tf.keras.losses.MSE(y_true, y_pred)return rc_loss

最后，我们将两个损失加在一起：

def vae_loss(y_true, y_pred):kl_loss = vae_kl_loss(y_true, y_pred)rc_loss = vae_rc_loss(y_true, y_pred)kl_weight_factor = 1e-2return kl_weight_factor*kl_loss + rc_loss

接下来，我们讨论一下 kl_weight_factor，它是 VAE 中经常忽略的重要超参数。如上所示，总损失由 KL 损失和重建损失组成。MNIST 数字的背景是黑色的，因此即使网络学到的知识很少，并且输出全为零，重建损失也相对较低。
相比较而言，潜变量的分布在开始时就遍布整个空间，因此减少 KLD 的收益要大于减少重建损失的收益。这鼓励网络忽略重建损失，仅针对 KLD 损失进行优化。结果，潜变量将具有 $N(0,1)$ 的理想标准高斯分布，但是生成的图像看起来与训练图像完全不同，这与生成模型的作用背道而驰。
编码器具有鉴别性，因为它会尝试找出图像中的差异。我们可以将每个潜变量视为一个特征。如果我们对 MNIST 数字使用两个潜变量，如果神经网络被迫使 KLD 损失为 0，则潜变量的分布将是相同的，因此，编码器失去了辨别能力。发生这种情况时，解码器每次都产生相同的图像，并且看起来像是平均像素值。

4. 使用 VAE 生成人脸图像

我们已经了解了 VAE 的理论并为 MNIST 构建了 VAE，接下来我们尝试增加难度。使用 VAE 生成人脸图像。常用人脸图像数据集包括：

• Celeb A，包含面部特征的注释，不能用于商业用途
• Flickr-Faces-HQ Dataset (FFHQ)，可免费用于商业用途，并包含高分辨率图像。

4.1 网络架构

鉴于人脸数据集与 MNIST 不同，我们需要对网络进行一些修改。可以修改层数，参数，图像大小，epoch 数和 batch 大小，具体修改如下：

• 将潜空间维度增加到 200
• 输入形状从 (28,28,1) 更改为 (112,112,3)，因为我们现在有 3 个颜色通道而不是灰度
• 在预处理管道中添加图像大小调整操作
• 添加更多的下采样层。在 MNIST 中，编码器两次下采样，从 28 降到 14，再降到 7。由于人脸图像分辨率更高，因此总共需要降采样四次
• 由于数据集更加复杂，增加卷积核数量以增加网络容量。因此，编码器中的卷积层如下。它与解码器相似，但方向相反：

  a) Conv2D(filters = 32, kernel_size=(3,3), strides = 2)
  b) Conv2D(filters = 32, kernel_size=(3,3), strides = 2)
  c) Conv2D(filters = 64, kernel_size=(3,3), strides = 2)
  d) Conv2D(filters = 64, kernel_size=(3,3), strides = 2)
  

尽管我们在网络训练中使用了 KLD 损失和重建损失，但我们仅应使用重建损失作为衡量何时保存模型和提前终止训练的指标。 KLD 损失可作为正则化，但我们对重构图像的质量更感兴趣。

4.2 人脸图像重建

重构图像如下所示：

尽管不是完美的重建，但它们的确看起来不错。VAE 设法从输入图像中学习了一些特征，并使用它们来绘制新的面孔。
由于图像背景的多样性，因此编码器无法将每个细节编码为低维度，我们可以看到 VAE 对背景颜色进行编码，而解码器则基于这些颜色创建模糊的背景。

4.3 生成新图像

为了生成新图像，我们从标准的高斯分布中创建随机向量，并将其提供给解码器：

z_samples = np.random.normal(loc=0, scale=1, size=(image_num, z_dim))
images = vae.decoder(z_samples.astype(np.float32))

我们可以使用采样技巧来提高图像保真度。

4.4 采样技巧

训练有素的 VAE 可以很好地重建人脸。但随机抽样产生的样本中并不完全合理，为了调试该问题，将数千张图像输入到 VAE 解码器中，以收集潜空间均值和方差。然后，绘制了每个潜空间变量的均值：

从理论上讲，它们应该以 0 为中心且方差为 1，但它们可能不是由于网络训练中 KLD 权重和随机性欠佳而引起的。因此，随机生成的样本并不总是与解码器期望的分布匹配。这是用来生成样本技巧的地方。使用与上述步骤相似的步骤，收集了潜变量的平均标准差(标量值)，该标准差用于生成正态分布的样本( 200 维)。然后，在其中添加了平均均值( 200 个维度)。

在下一节中，我们将学习如何执行人脸图像编辑，而不是生成随机人脸图像。

5. 控制人脸属性

5.1 潜空间算法

我们已经多次讨论了潜空间，但没有给它一个适当的定义。本质上，它表示潜变量的每个可能值。在我们的 VAE 中，它是 200 个维度的向量，或者仅仅是 200 个变量。我们希望每个变量对我们都有独特的语义含义，例如 z[0] 代表眼睛，z[1] 代表眼睛的颜色，依此类推。我们只需要假设信息是在所有潜向量中编码的，就可以使用向量算术探索空间。
在进入高维空间之前，让我们尝试使用一个二维示例来理解它。假设现在我们在地图上的 (0,0) 点，而目的地位于 (x, y)。因此，朝目的地的方向是 (x-0, y-0) 除以 (x, y) 的 L2 范数，或者将方向表示为 (x_dot, y_dot)。因此，每当移动 (x_dot, y_dot) 时，我们就是在朝着目的地移动。当移动 (-2 * x_dot, -2 * y_dot) 时，我们将以两倍的步数远离目的地。
现在，如果我们知道了微笑属性的方向向量，则可以将其添加到潜变量中以使人脸图像带有微笑：

new_z_samples = z_samples +  smiling_magnitude*smiling_vector

smile_magnitud e是我们设置的标量值，因此下一步是找出获取 smile_vector 的方法。

5.2 查找属性向量

某些数据集(例如 Celeb A) 附带每个图像的面部属性注释。标签是二进制的，表示它们指示图像中是否存在特定属性。我们将使用标签和编码的潜变量来找到我们的方向向量：

• 使用测试数据集或训练数据集中的样本，并使用 VAE 解码器生成潜矢量
• 将潜\向量分为两组：具有(正)或不具有(负)的我们感兴趣的一个属性
• 分别计算正向量和负向量的平均值
• 通过从平均正向量中减去平均负向量来获取属性方向向量

修改预处理函数，以返回我们感兴趣的属性的标签。然后，我们使用 lambda 函数映射到数据管道：

def preprocess_attrib(sample, attribute):image = sample['image']image = tf.image.resize(image, [112,112])image = tf.cast(image, tf.float32)/255.return image, sample['attributes'][attribute]
ds = ds.map(lambda x: preprocess_attrib(x, attribute))

不要与将任意 TensorFlow 函数包装到 Keras 层中的 Keras Lambda 层相混淆，代码中的 lambda 是通用的 Python 表达式。lambda 函数用作一个小函数，但没有用于定义该函数的代码。前面的代码中的 lambda 函数等效于以下函数：

def preprocess(x):  return preprocess_attrib(x, attribute))

将映射链接到数据集时，数据集对象将顺序读取每个图像，并调用与 preprocess(image) 等效的 lambda 函数。

5.3 人脸图像编辑

提取属性向量后，我们现在可以进行以下操作：

• 首先，我们从数据集中获取图像，该图像是以下屏幕截图中最左侧的面孔
• 我们将人脸编码为潜变量，然后对其进行解码以生成新人脸，并将其放置在行的中间
• 然后，我们向右逐渐增加属性向量
• 同样，我们向行的左侧减去属性向量

以下屏幕快照显示了通过内插 Young 的潜向量生成的图像：

这些属性不是互斥的。例如，随着我们增加女性的 moustache 属性，其肤色和头发变得更像男人，这是完全合理的，实际上是我们想要的。这表明某些潜变量分布重叠。