AVLTree(C++ Version)
文章目录
- 一、AVL树概念
- 二、AVL树插入
一、AVL树概念
1.AVL树是一颗高度平衡二叉搜索树(通过控制左右子树的高度来控制二叉搜索树的平衡)
2.AVL树的要求:
(1)AVL树可以是一颗空树
(2)当AVL树不是空树时,要求AVL树的左右子树的高度差的绝对值不超过1
并且AVL树的子树也要求是一颗AVL树(左右子树的高度差的绝对值不超过1)
AVL树的左右子树高度差只能为-1 / 0 / 1,AVL树的子树的左右子树高度差只能为-1 / 0 / 1
3.为什么AVL树的要求是左右子树的高度差的绝对值不超过1,而不是左右子树的高度差为0
左右子树的高度差的绝对值为0时,不是更加平衡嘛?
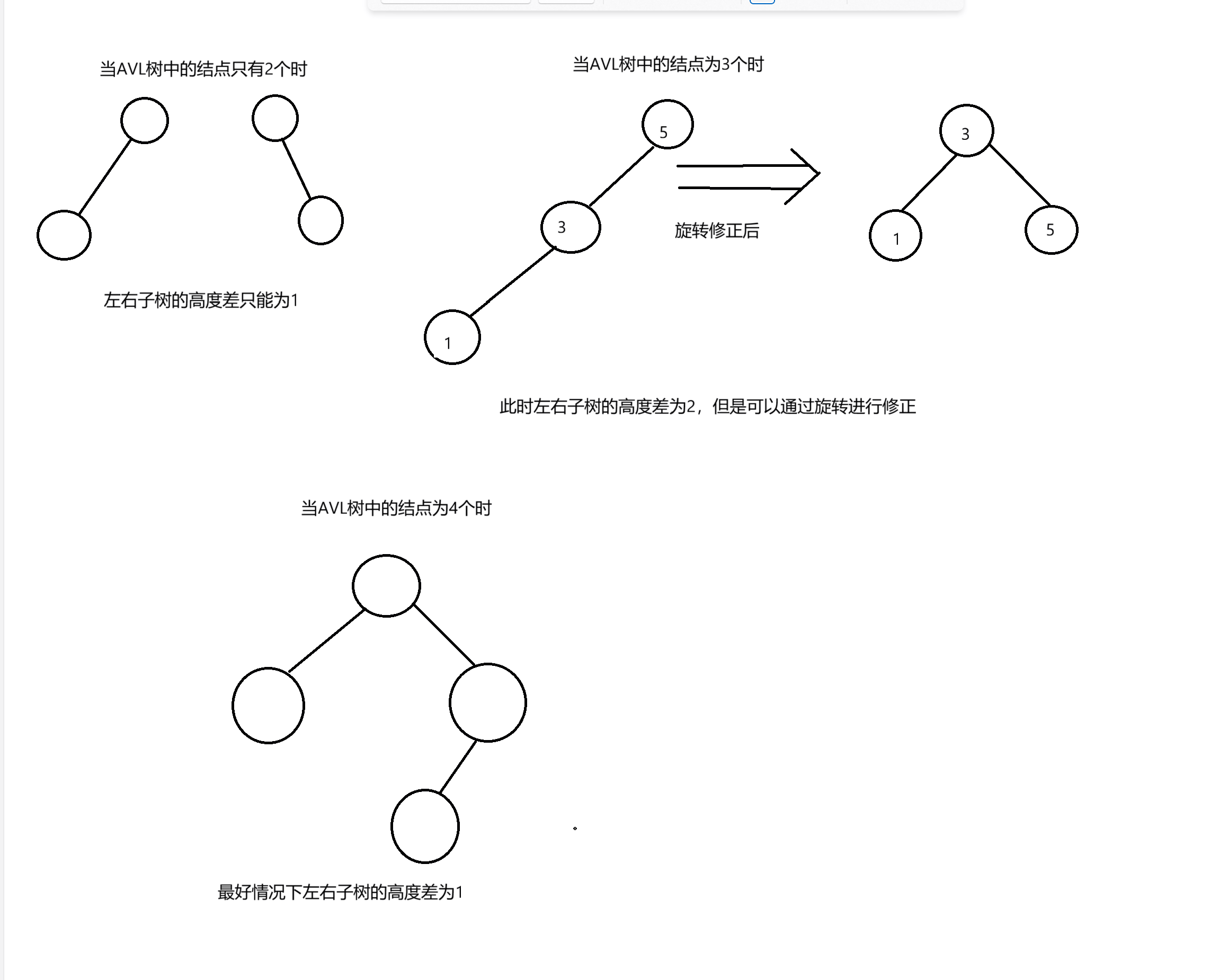
(1)当AVL树中的结点个数为2,那么AVL树的左右子树的高度差只能为1
(2)当AVL树中的结点个数为3,并且使得左右子树高度差为2时,是可以通过旋转修正
为左右子树的高度差为0
(3)当AVL树中的结点个数为4,最好情况下左右子树的高度差为1
(4)所以左右子树的高度差的绝对值不超过1时,就是最好平衡
4.平衡因子
(1)AVL树中的每一个结点都会引入一个平衡因子
(2)平衡因子 == 右子树高度 - 左子树高度
(3)平衡因子可以帮助我们更好的观测到AVL树是否平衡
可以直观的观察到AVL树中的每一刻子树的左右子树的高度差的绝对值是否不超过1
(4)因为平衡因子 == 右子树的高度 - 左子树的高度,AVL左右子树的高度差的绝对值
不超过1,所以平衡因子符合规则的取值范围为-1 / 0 / 1
(5)实现AVL树平衡因子不是必须的
5.AVL树整体的结点数量的分布和完全二叉树相似,高度可以控制在logN
那么增删查改的时间复杂度也可以控制在logN
相比二叉搜索树有了本质的提升
二、AVL树插入
1.AVL树的结构
(1)AVL树结点的结构
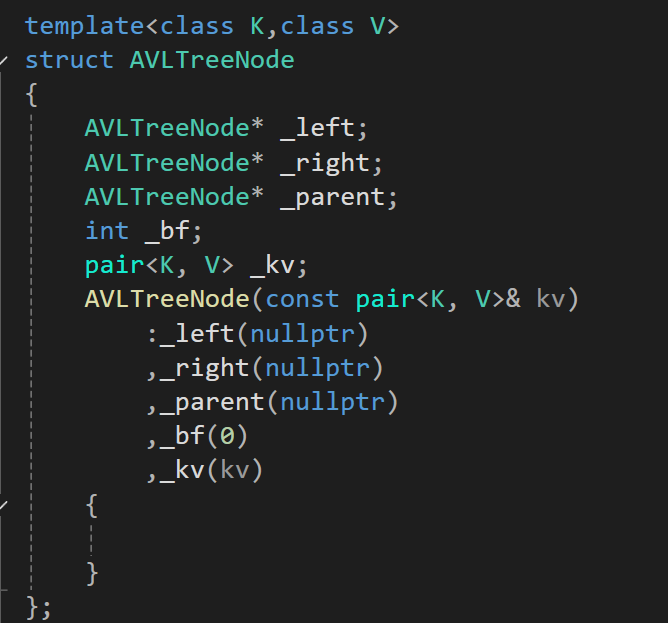
_parent是该结点的父结点,添加父结点是为了在插入后可以找到父结点去更新
父结点中的平衡因子,不过需要注意添加了_parent就是三叉链,那么在插入新
结点之后就需要更新_parent
_bf是该结点的平衡因子 == 右子树的高度 - 左子树的高度
新增结点的左右子树都为空,所以新增结点的平衡因子 == 0
使用pair实现key_value的结构
(2)AVL树结构
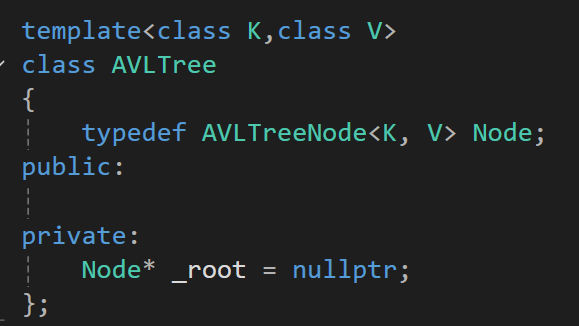
在新创建一颗AVL树时,该AVL树为一颗空树,那么只需要将_root初始化为nullptr
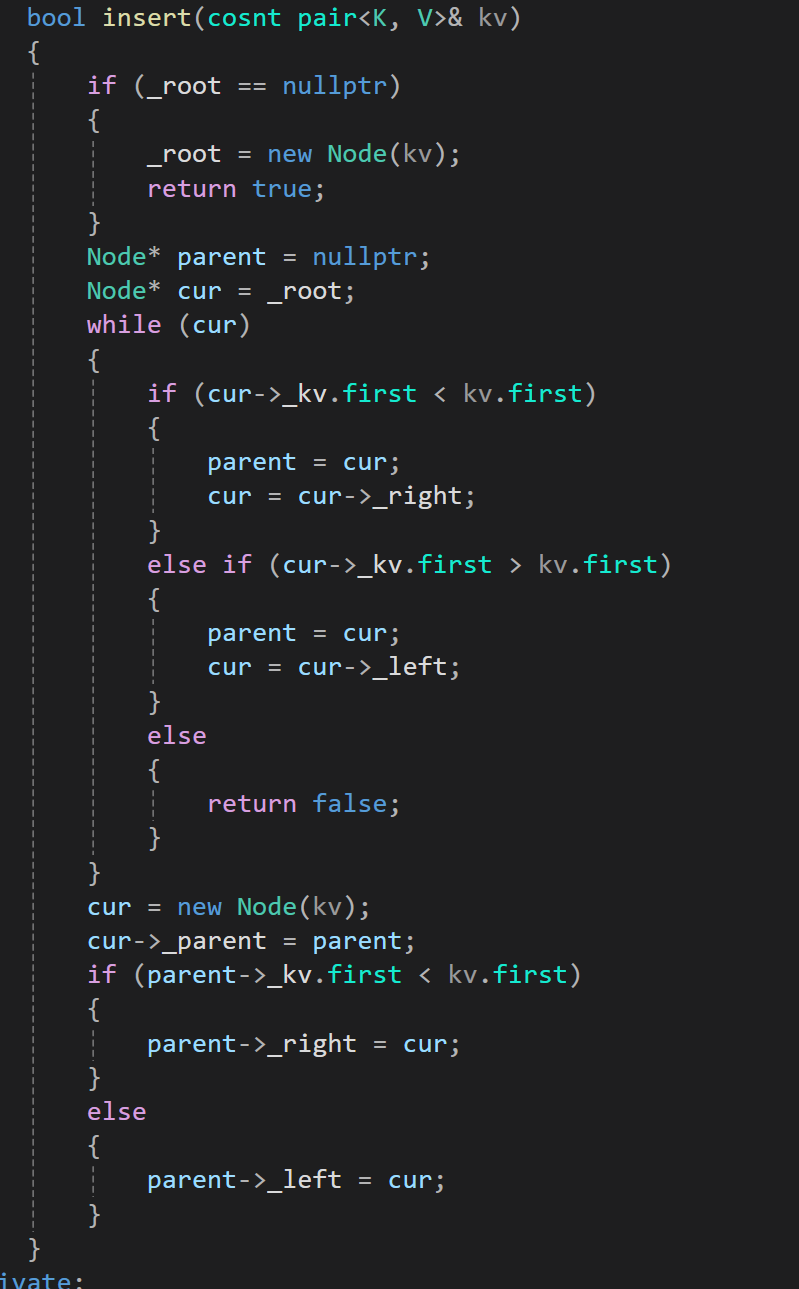
2.插入
(1)因为AVL树本质上是一颗二叉搜索树,那么AVL树的插入就需要根据二叉搜索树的
规则进行插入
(2)如果_root为空,那么新增结点就是根结点,直接插入就可以
(3)如果_root不为空,那么就需要创建Node* cur = _root;以及Node* parent = nullptr
创建parent变量是为了找到插入的位置之后,可以通过parent锁定其父亲,将其链接起来
从根结点开始比较,找到新增结点应该插入的位置
如果插入的key大于当前结点中的key,那么cur就往右走
如果插入的key小于当前结点中的key,那么cur就往左走
3.平衡因子更新
(1)平衡因子 == 右子树的高度 - 左子树的高度
那么影响子树的高度就会影响平衡因子
(2)新增结点肯定会将子树的高度提升的
那么新增一个结点肯会影响_parent的平衡因子
而_parent又可能会是其他结点的子树,那么就又会影响_parent的_parent的平衡因子
那么插入一个新的结点,就会影响该结点的祖先路径上结点的平衡因子
(3)新增结点,就会增加高度,所以新增结点在parent的右子树,parent的平衡因子++
新增结点在parent的左子树,parent的平衡因子--
(4)parent所在的子树的高度是否变化决定了是否继续向上更新
4.更新停止的条件
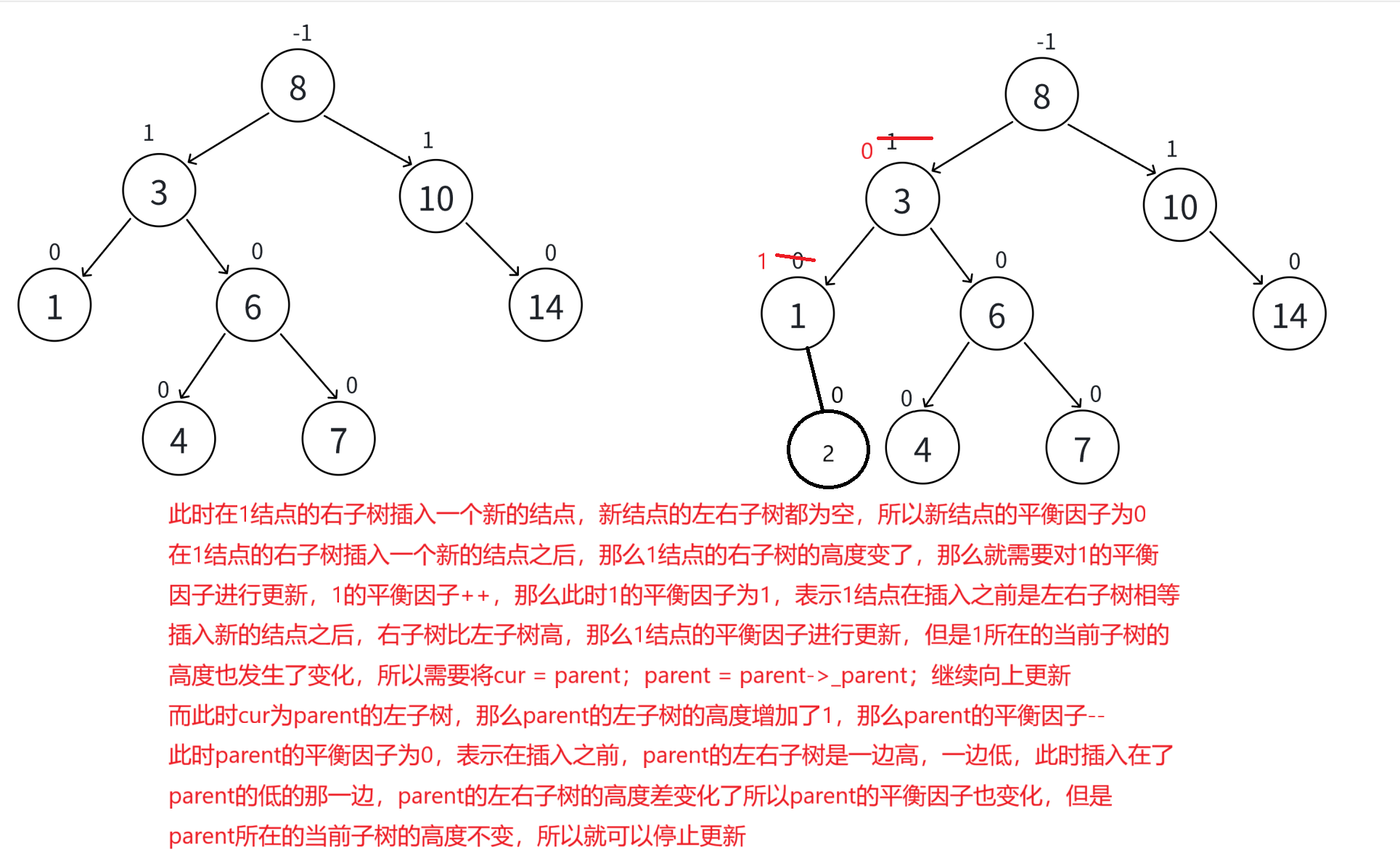
(1)当更新该结点的平衡因子之后,此时该结点的平衡因子 == 0,那么就停止更新
因为要想该结点的平衡因子更新之后为0,那么该结点的平衡因子在更新之前就为-1 / 1
那么就表示该结点的左右子树是一边高,一边低,那么此时是插入在了低的那一边,
该结点的左右子树的高度变化了,该结点的平衡因子进行更新
但是该结点所在的子树的整体高度不变
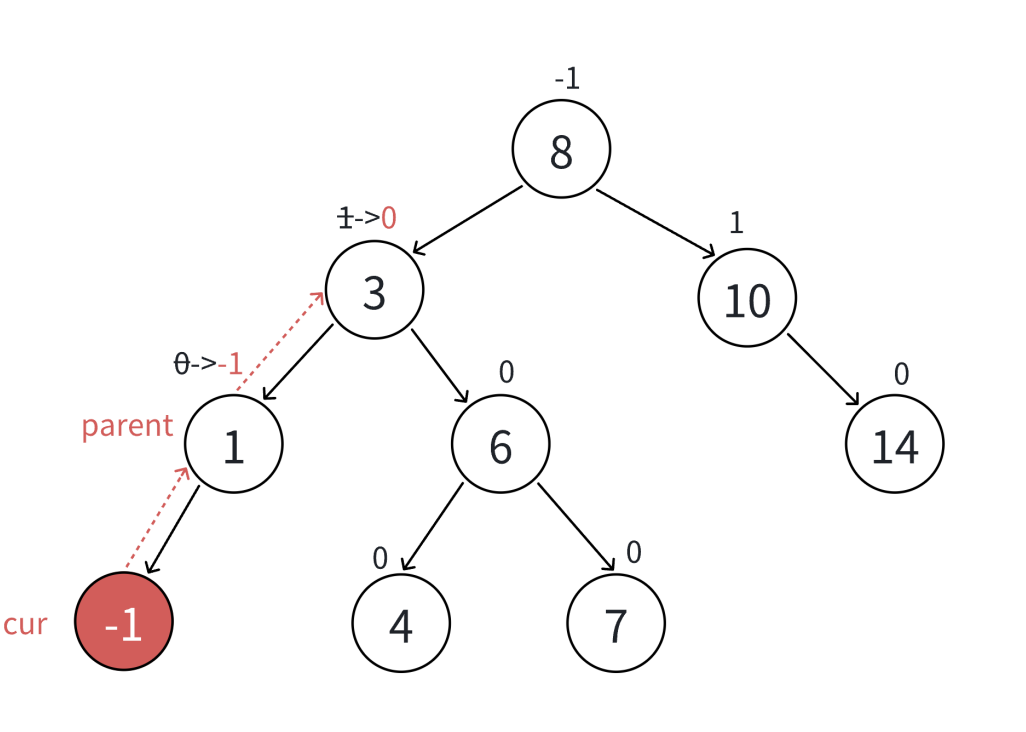
(2)当更新该结点的平衡因子之后,此时该结点的平衡因子 == -1/ 1
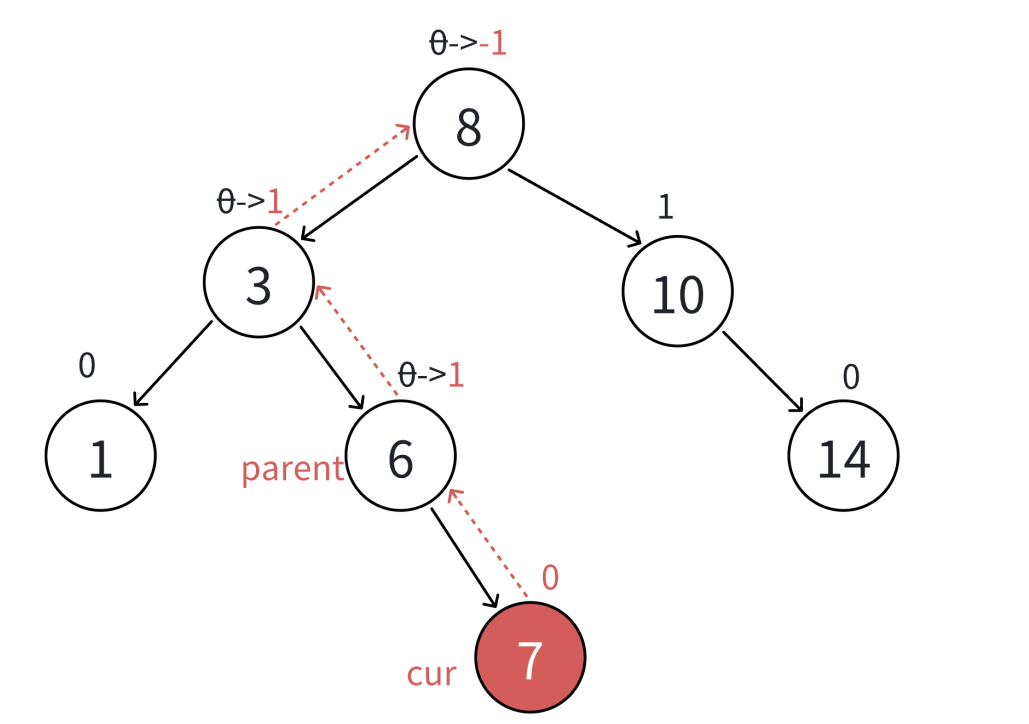
那么就将cur = parent;parent = parent->_parent;继续向上更新
因为想要该结点的平衡因子更新之后为-1/ 1,那么该结点在更新平衡因子之前就为0
那么就表示该结点的左右子树的高度相等,此时是在左右子树的其中一颗子树插入的
该结点的左右子树的高度变化了,该节点的平衡因子进行更新
但是该结点所在的子树的整体高度也变化了,所以需要继续向上更新
最坏不断更新,更新到根,根的平衡因子为-1 / 1也就停止了
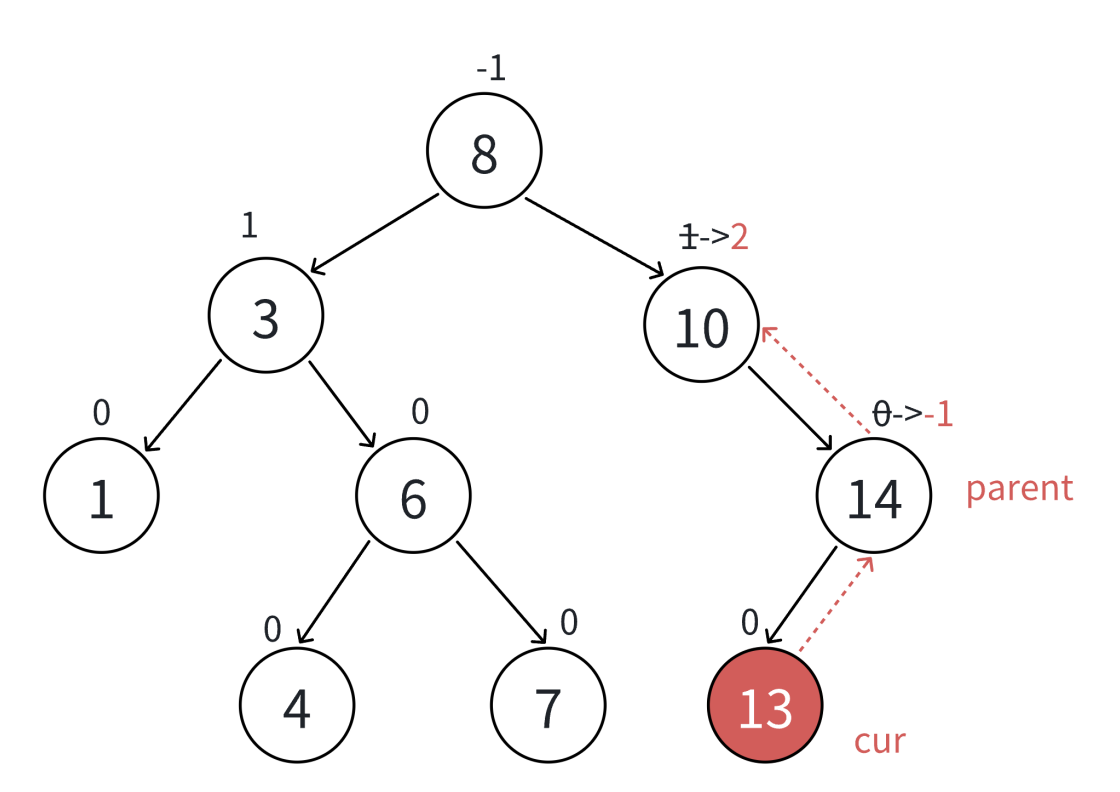
(3)当更新平衡因子之后,此时该结点的平衡因子为-2 / 2,停止更新
通过旋转将其进行修整,因为平衡因子为-2 / 2就已经违反了AVL树的规则
当更新该结点的平衡因子之后,该结点的平衡因子为-2 / 2那么就表明
在插入新的结点之前,该结点的左右子树的高度差已经为1了,一边高,一边低
而插入新的结点,又插入在了高的那一边,parent子树高的那一边更高了,
破坏了平衡,此时通过旋转将其进行修正
(4)代码实现
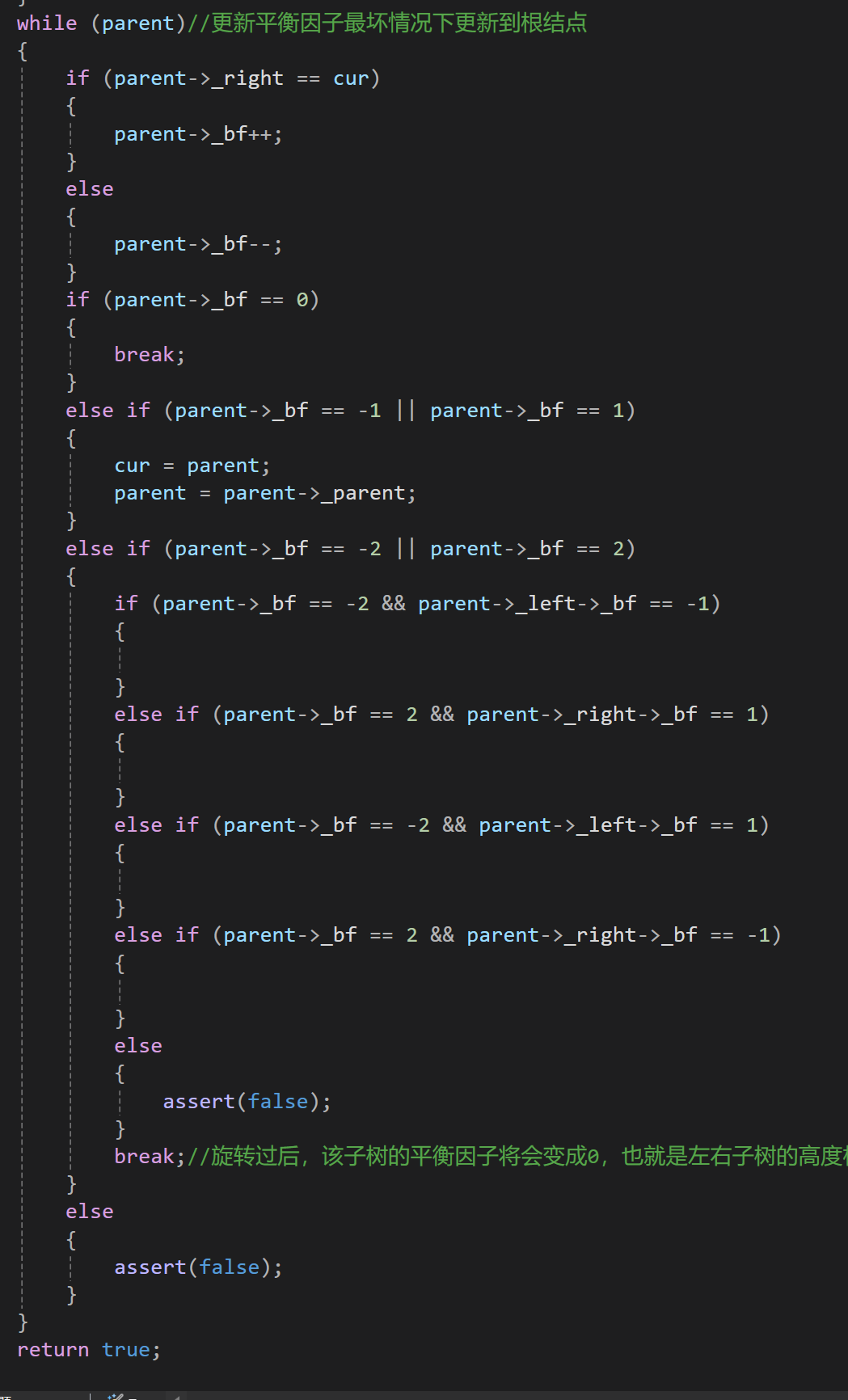
5.旋转
(1)右单旋
当该结点的平衡因子为-2以及该结点的_left的平衡因子为-1时
也就是单纯的左边高,使用右单旋
a.该结点平衡因子更新之后为-2,表明在更新平衡因子之前,该结点的平衡因子为-1,
表明插入之前,该结点左子树比右子树高1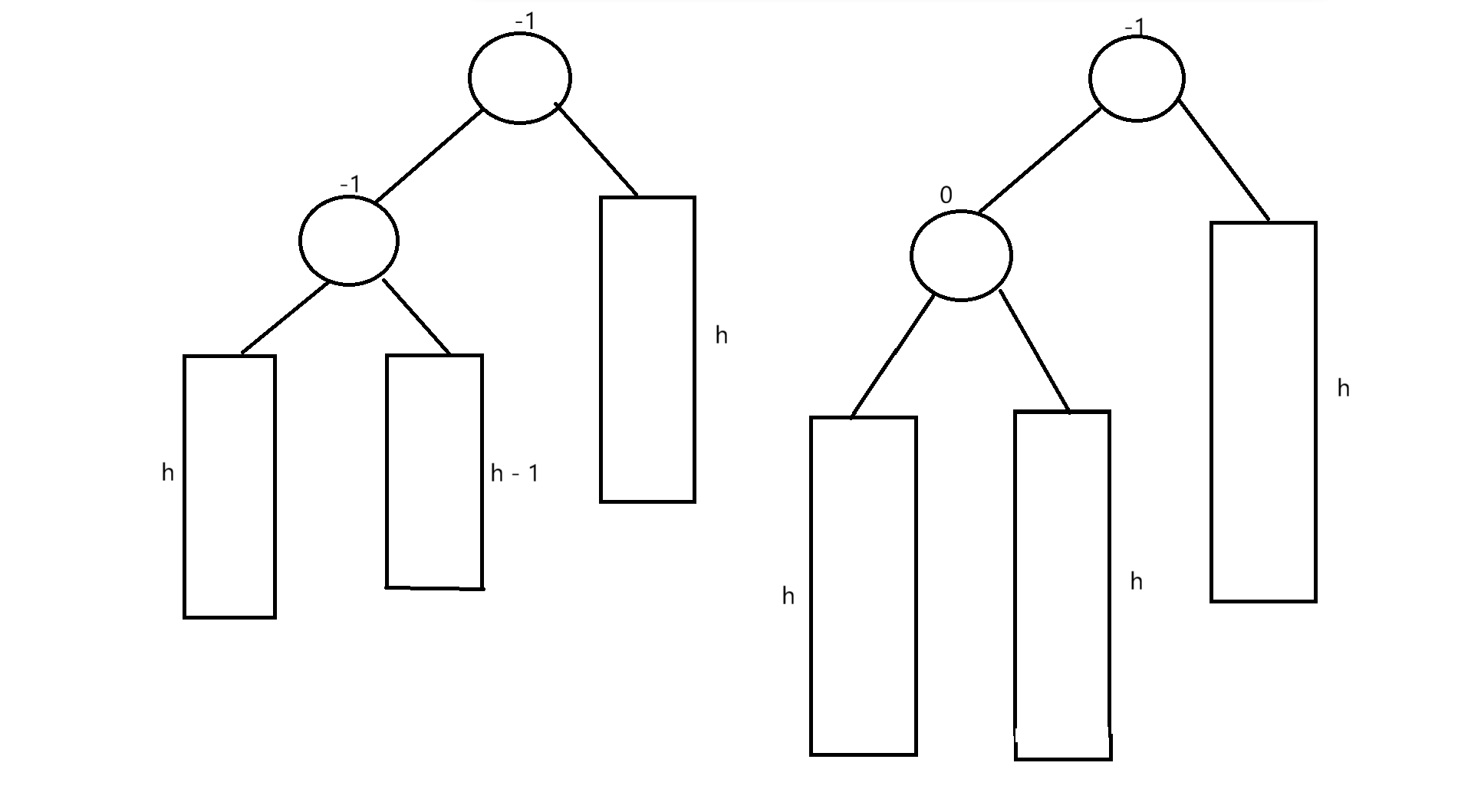
b.此时该结点的平衡因子为-1,那么想要使得该结点的平衡因子由-1 -> -2
那么就需要在左子树进行插入
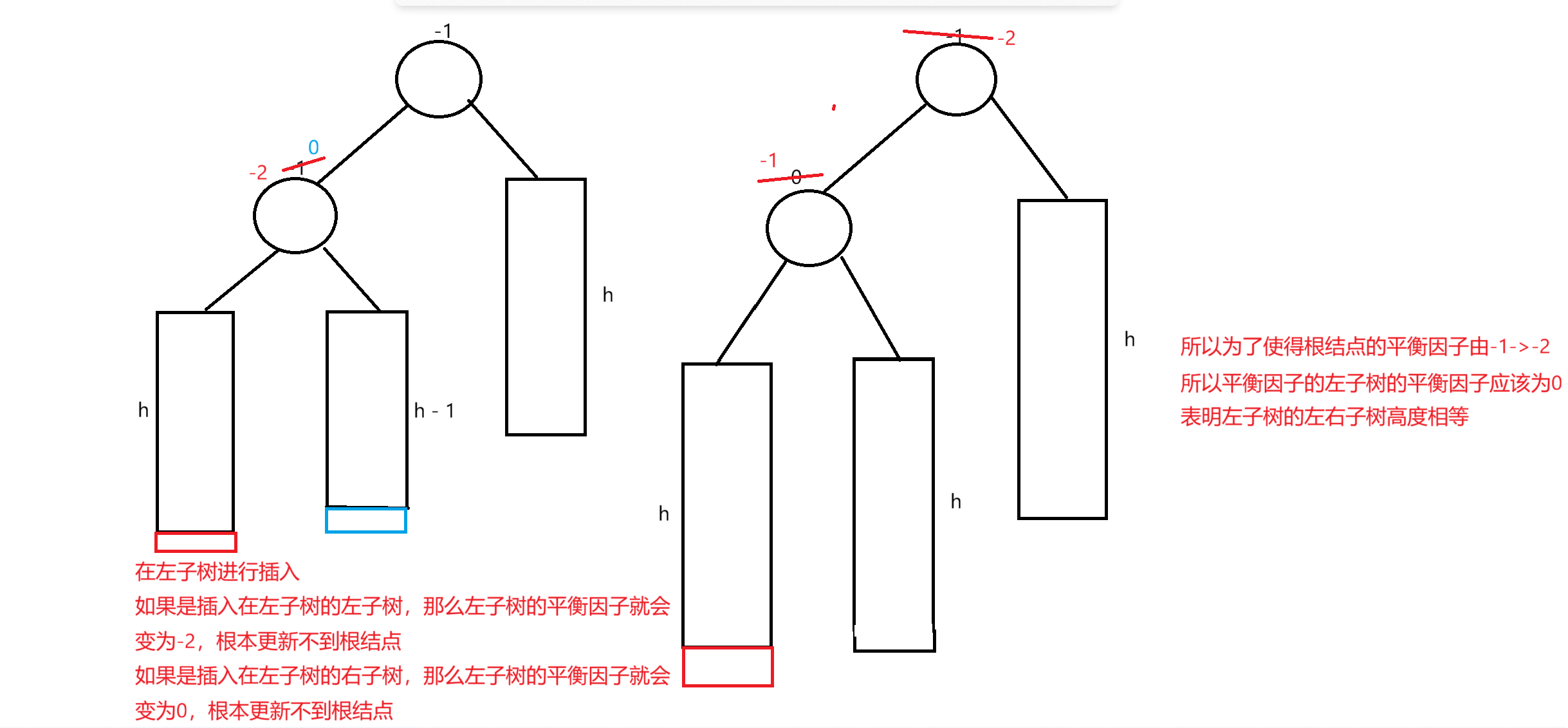
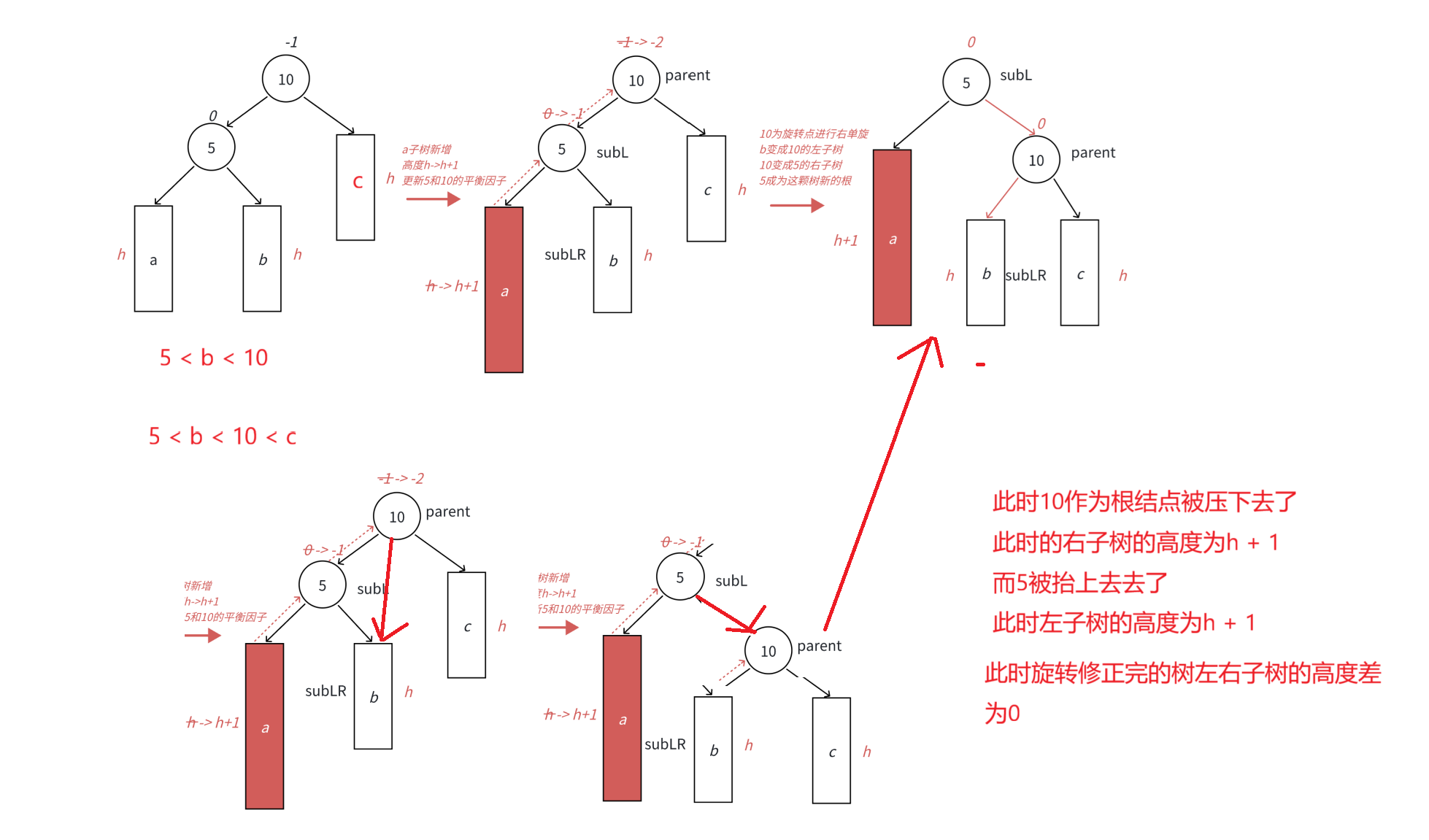
c.此时是左子树右子树的高度差为2,那么为了使得这一颗树平衡,我们需要
将左子树的右子树作为根结点的左子树,然后将根连带着新的左子树和右子树压下去
作为左子树的右子树,那么此时右子树的高度为h + 1
然后将左子树的根结点作为整颗树的根结点抬上来,此时左子树的高度为h + 1
此时左右子树的高度差就为0,左右子树的高度相等
并且在插入之前整棵树的高度为h + 2,旋转修正完的整棵树的高度也为h + 2
所以并不需要继续往上调整平衡因子
d.代码实现
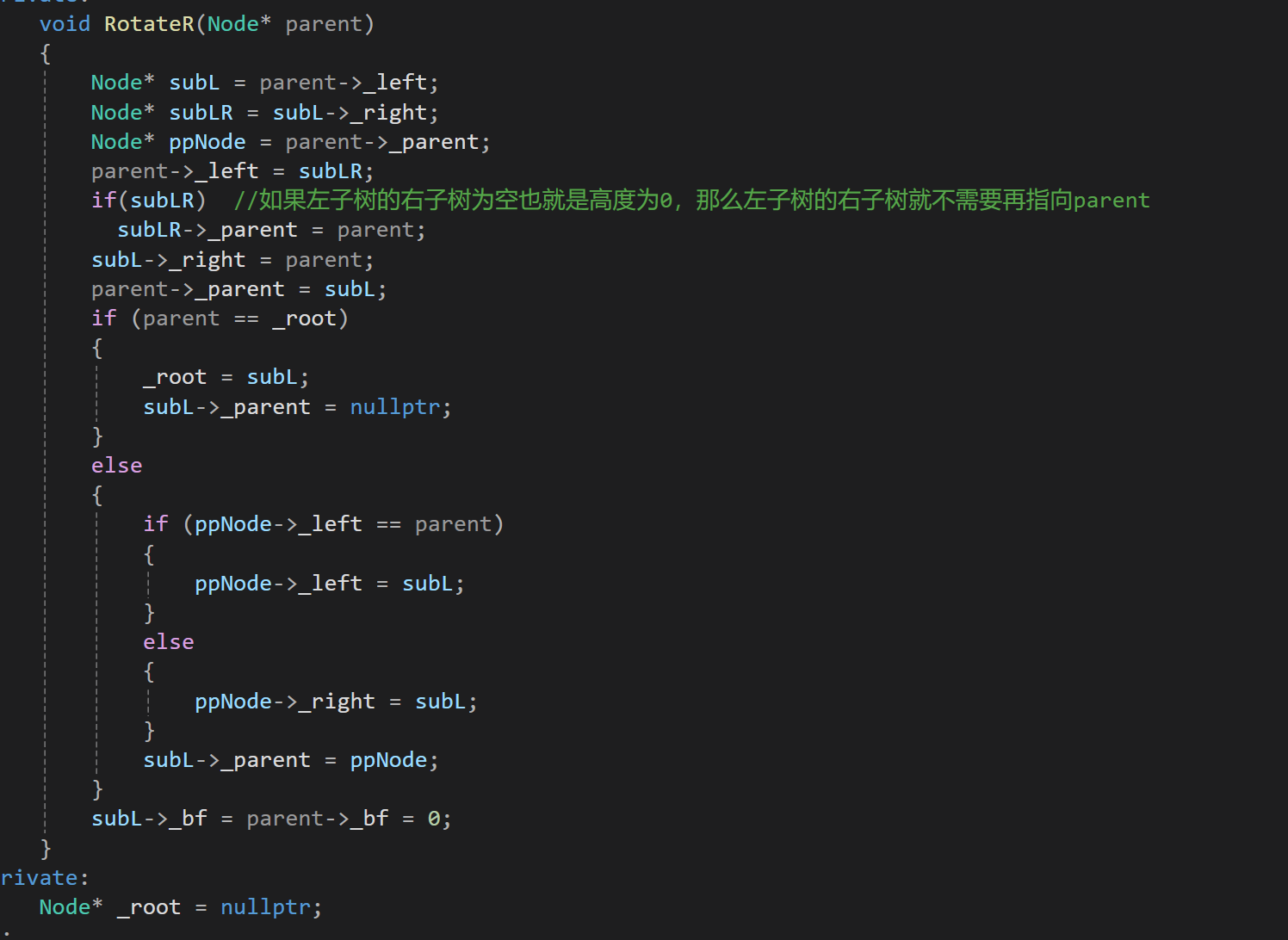
(2)左单旋
当该结点的平衡因子为2时以及该结点的右子树的根结点的平衡因子为1时
也就是单纯的右边高,使用左单旋
a.当该结点的平衡因子更新之后为2,那么就表明该结点在更新平衡因子之前为1
表明右子树比左子树高1
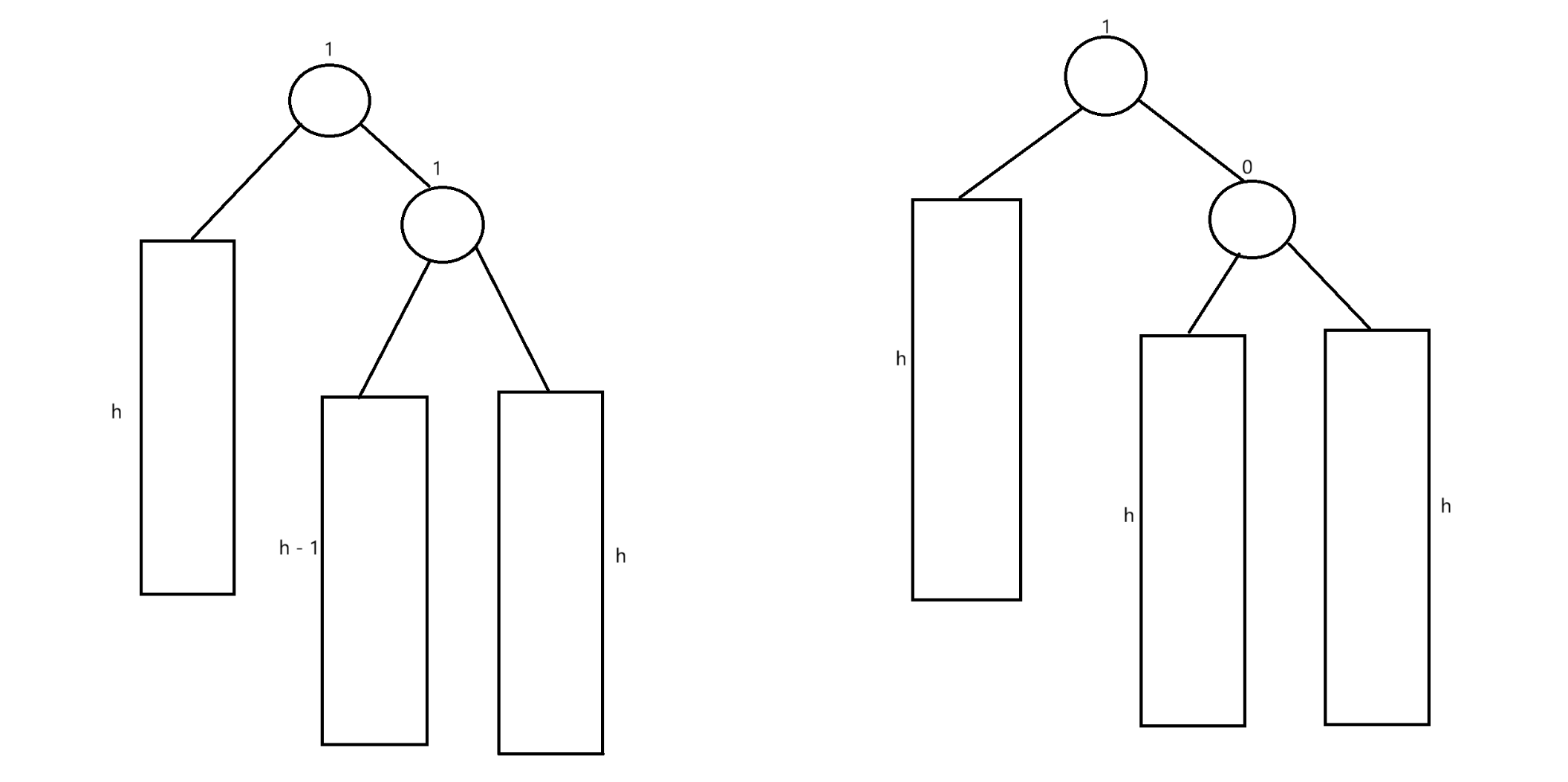
b.此时该结点的平衡因子为1,那么想要使得该结点的平衡因子由1 -> 2
那么就需要在右子树进行插入
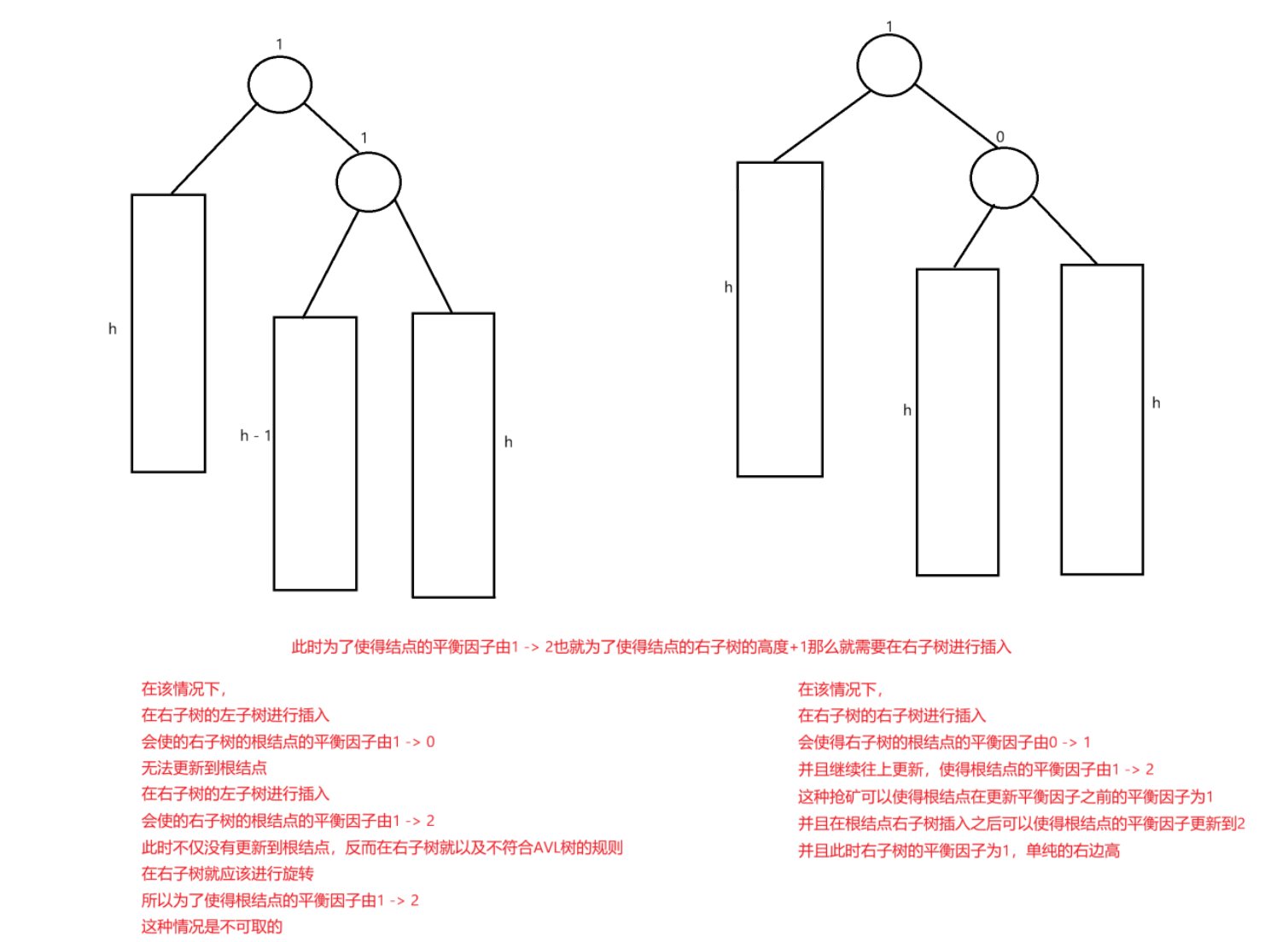
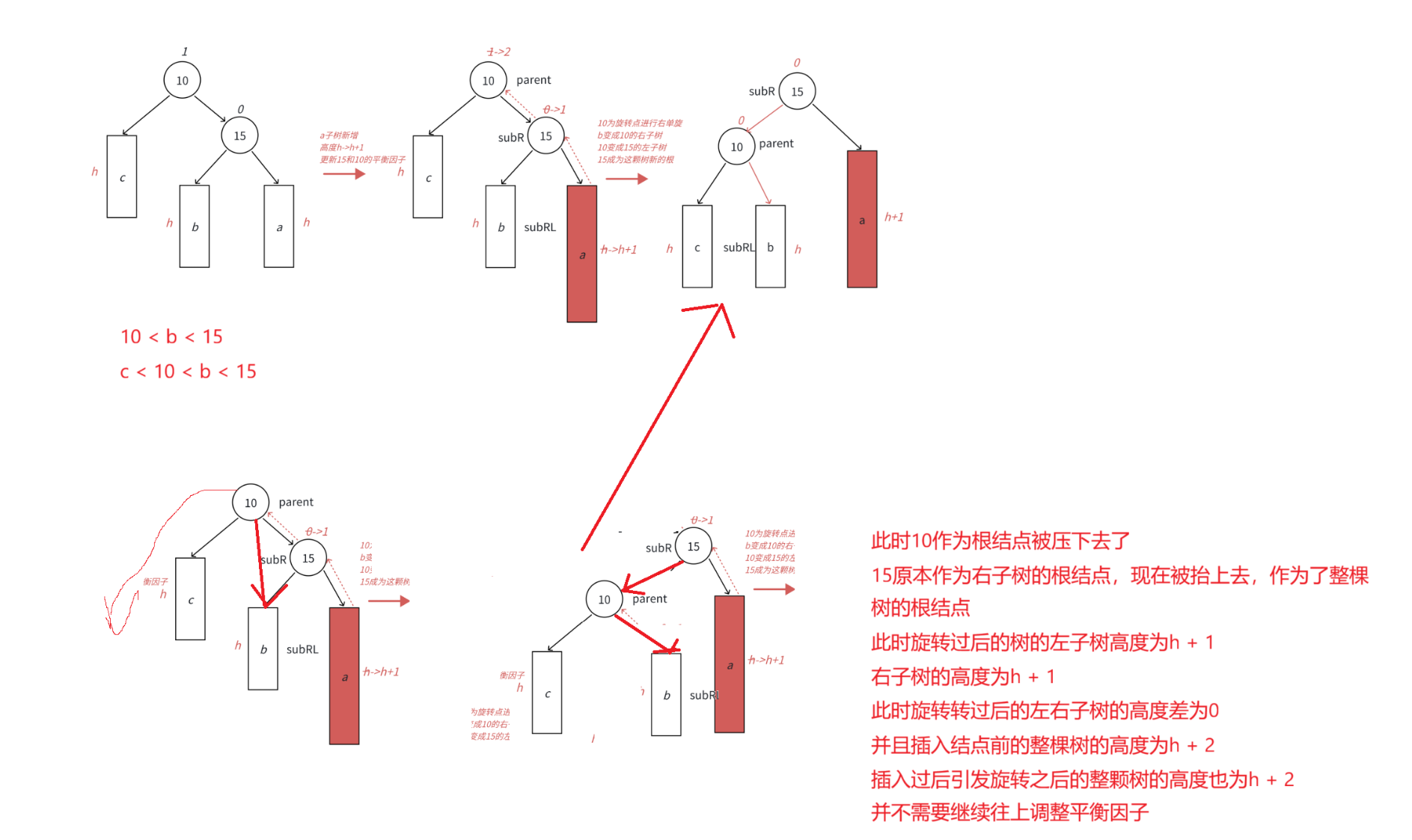
c.此时该结点的左右子树的高度差为2,为了使得这一颗树平衡,我们需要
将右子树的左子树给根结点的右子树,再将根结点作为右子树的左子树
将根结点往下压,将右子树往上抬,此时右子树的根结点作为整棵树的根结点
此时原本的根结点以及他目前的左右子树作为了新的根结点的左子树,高度为h + 1
原本的右子树的根结点作为了在目前整棵树的根结点,此时他的右子树高度为h + 1
此时通过旋转调整过后的树,左右子树的高度皆为h + 1,左右子树高度差为0,很平衡
并且添加新结点之前的整棵树的高度为h + 2,旋转修正后的高度也为h + 2
所以如果该树是其他树的子树,那么也不需要继续向上调整其_parent平衡因子
d.代码实现
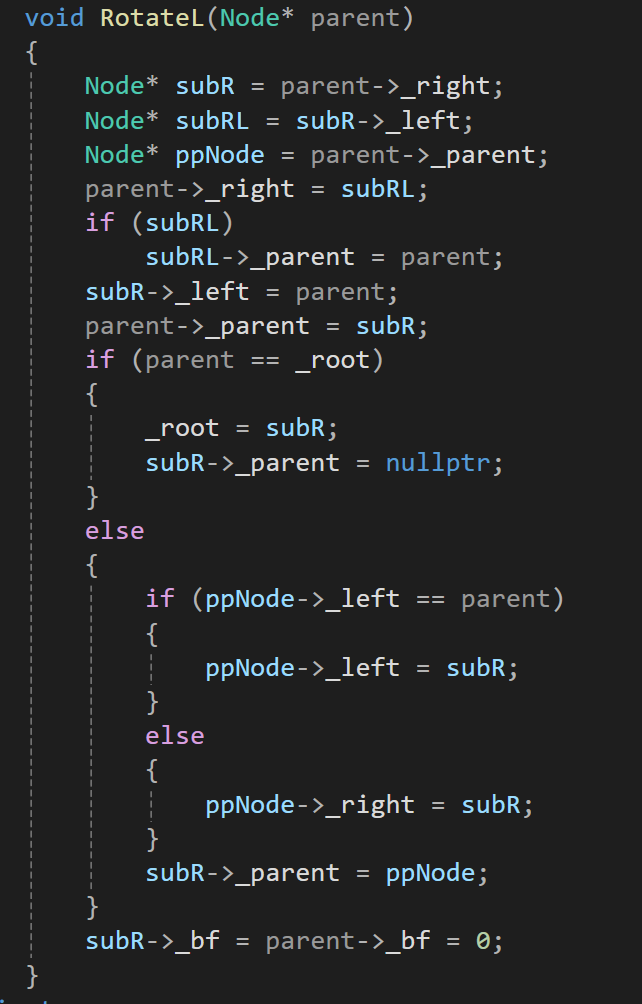
(3)左右双旋
当该结点的平衡因子为-2并且左子树的根结点的平衡因子为1,左边高的右边高
使用左右双旋进行旋转
a.该结点更新平衡因子之后为-2,表明在该结点更新平衡因子前该结点的平衡因子为
-1,左子树比右子树高1,并且新增结点是新增在该结点的左子树往上更新平衡因子时
将平衡因子更新为-2
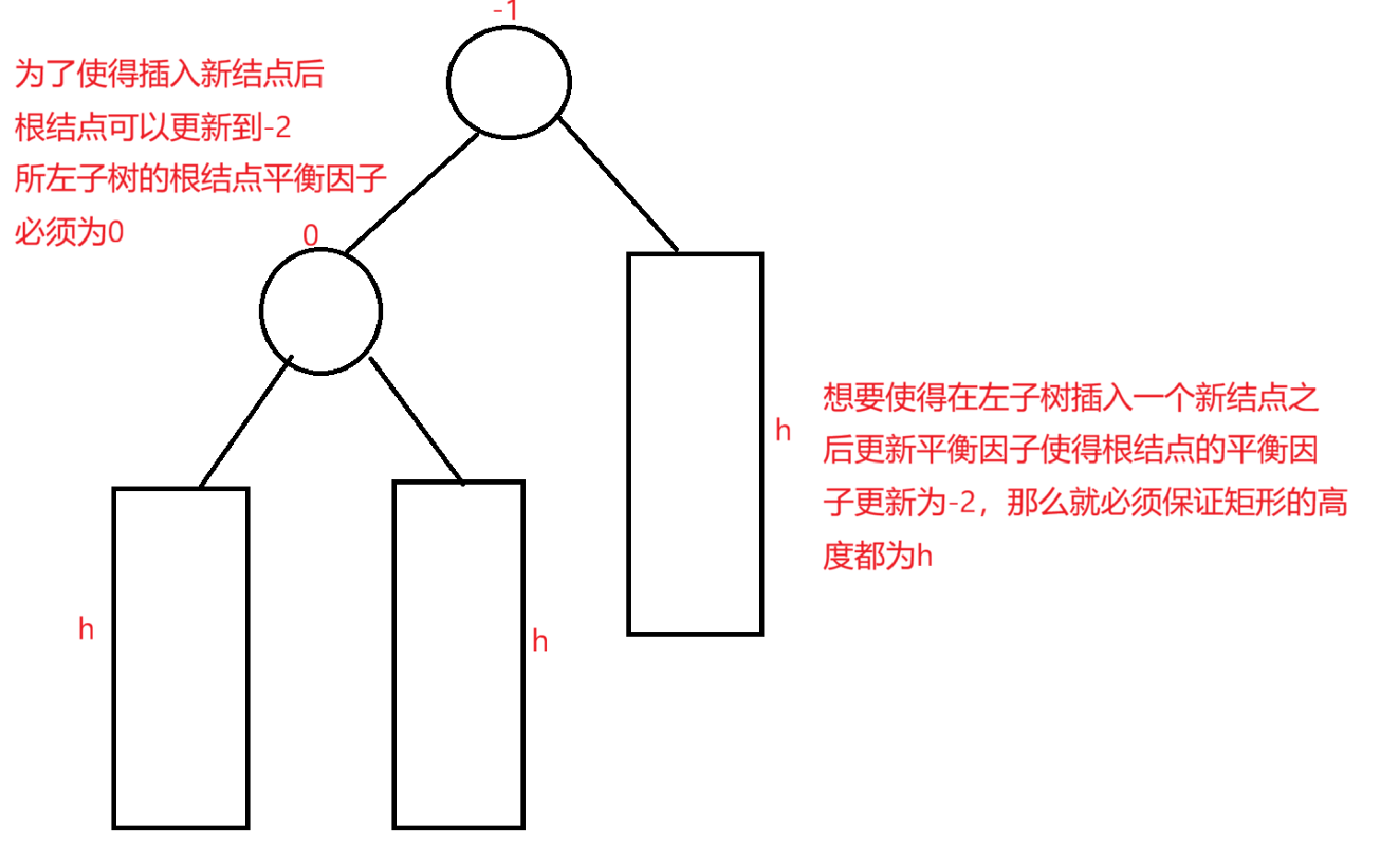
b.要使得插入之后更新的根结点平衡因子为-2,根结点的左子树的根结点为1
那么就必须在左子树的右子树中插入新的结点,如果此时使用单旋,就会变为
右边高的左边高,所以不可以使用单旋
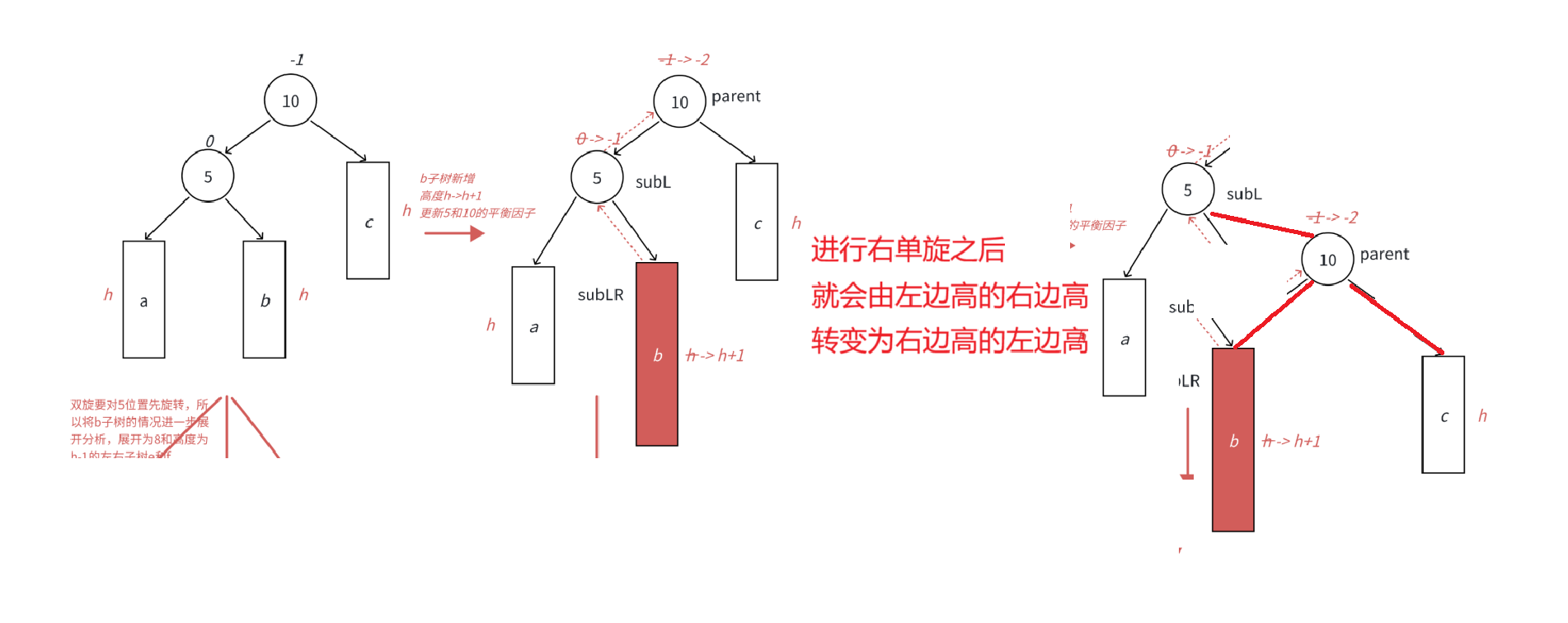
c.左右双旋本质上是使用两次单旋
逻辑上是:左边高的右边高不会旋转,但是左边高的左边高会啊不就是右单旋
所以首先需要使用一次左单旋使得左边高的右边高变为左边高的左边高
然后再对左边高的左边高采用右单旋
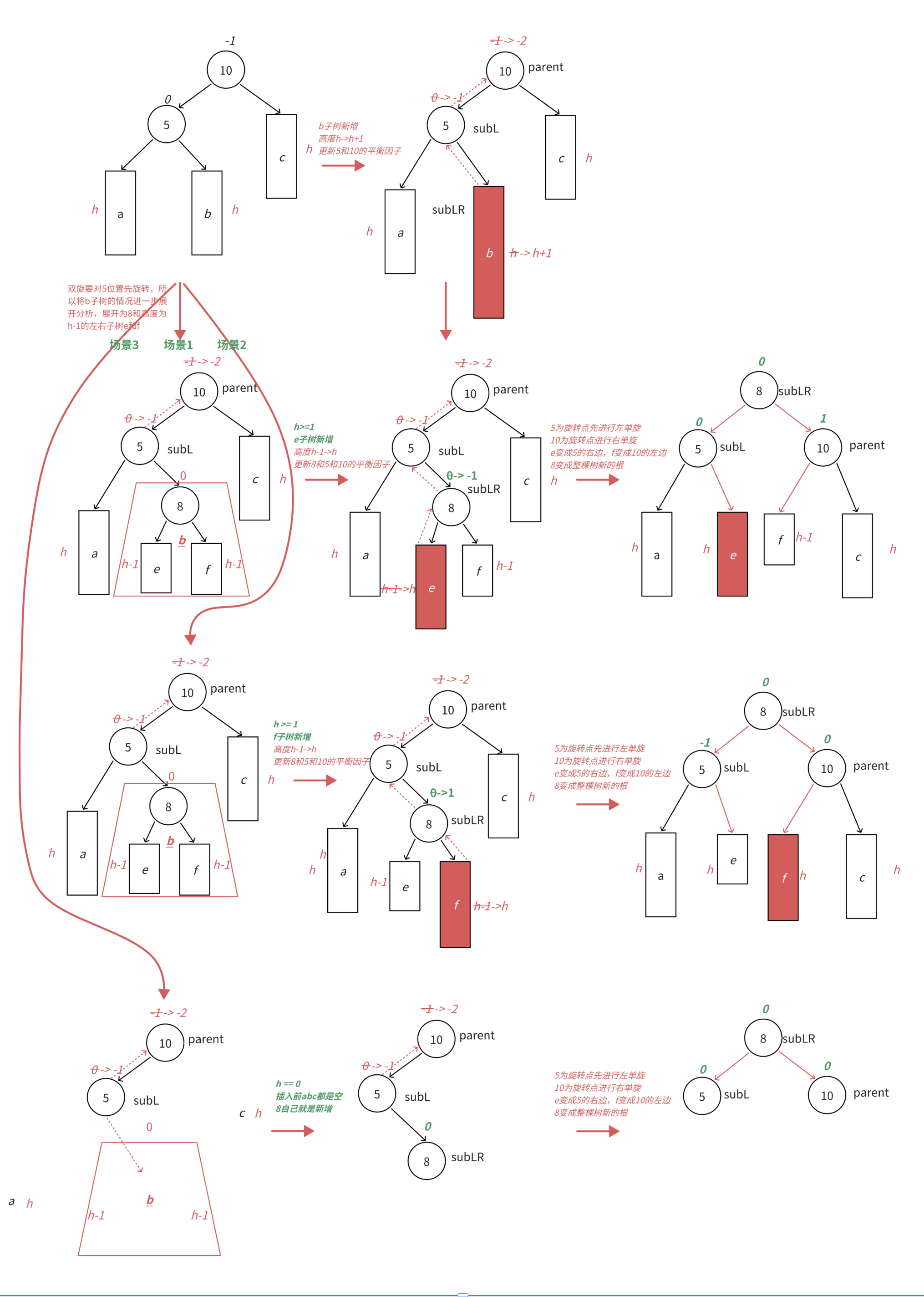
以下图为例:
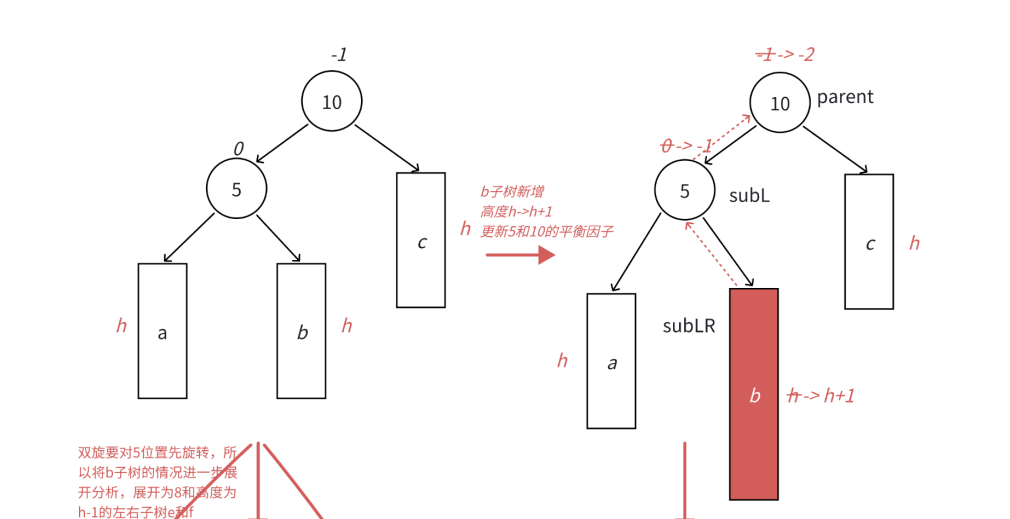
首先将5进行左旋转,将b的左子树作为5的右子树,然后5作为b的左子树
然后对10进行右旋转,将b的右子树作为10的左子树,然后10作为b的右子树
此时双旋就讨论到了b的左右子树,所以b必须展开讨论
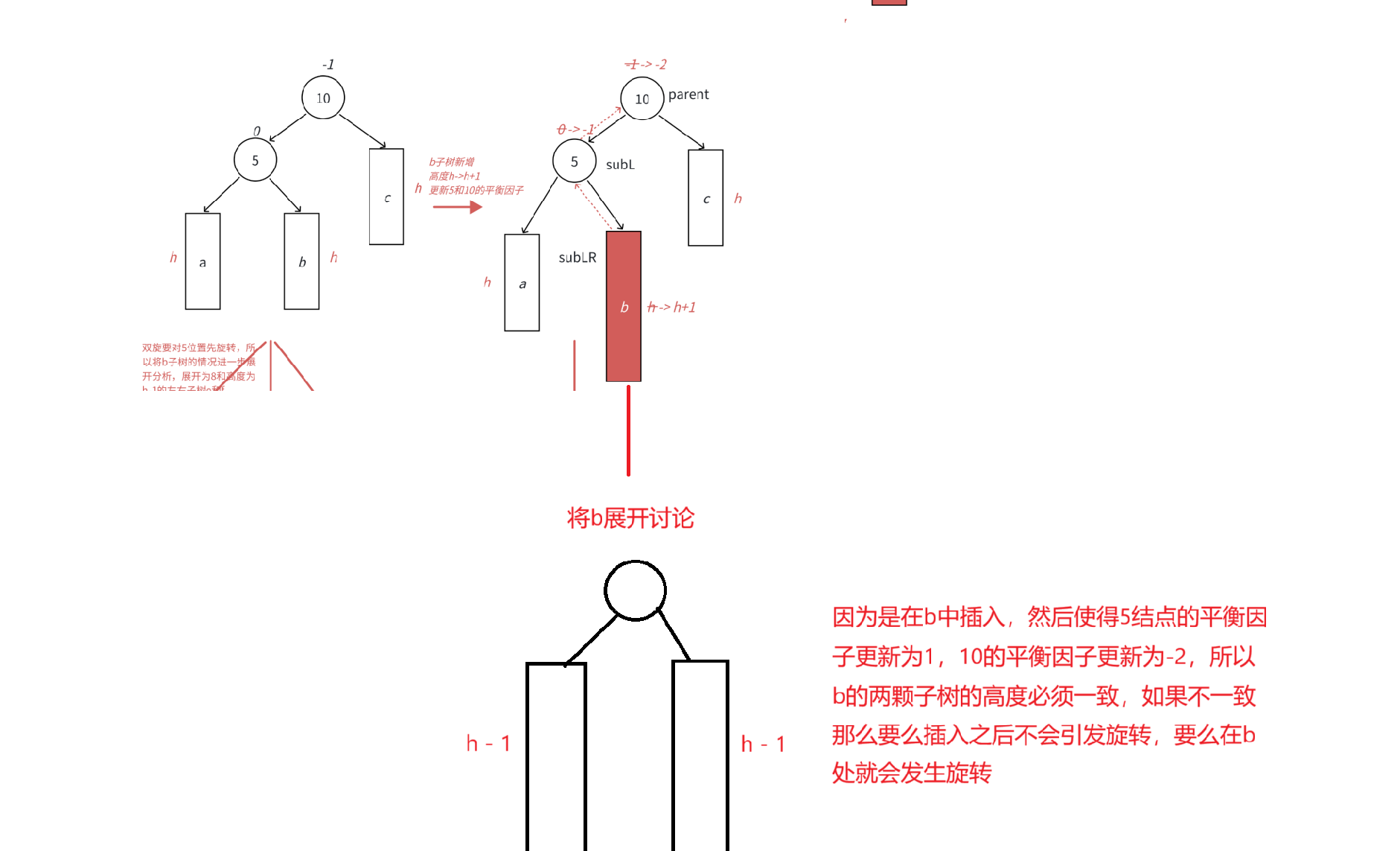
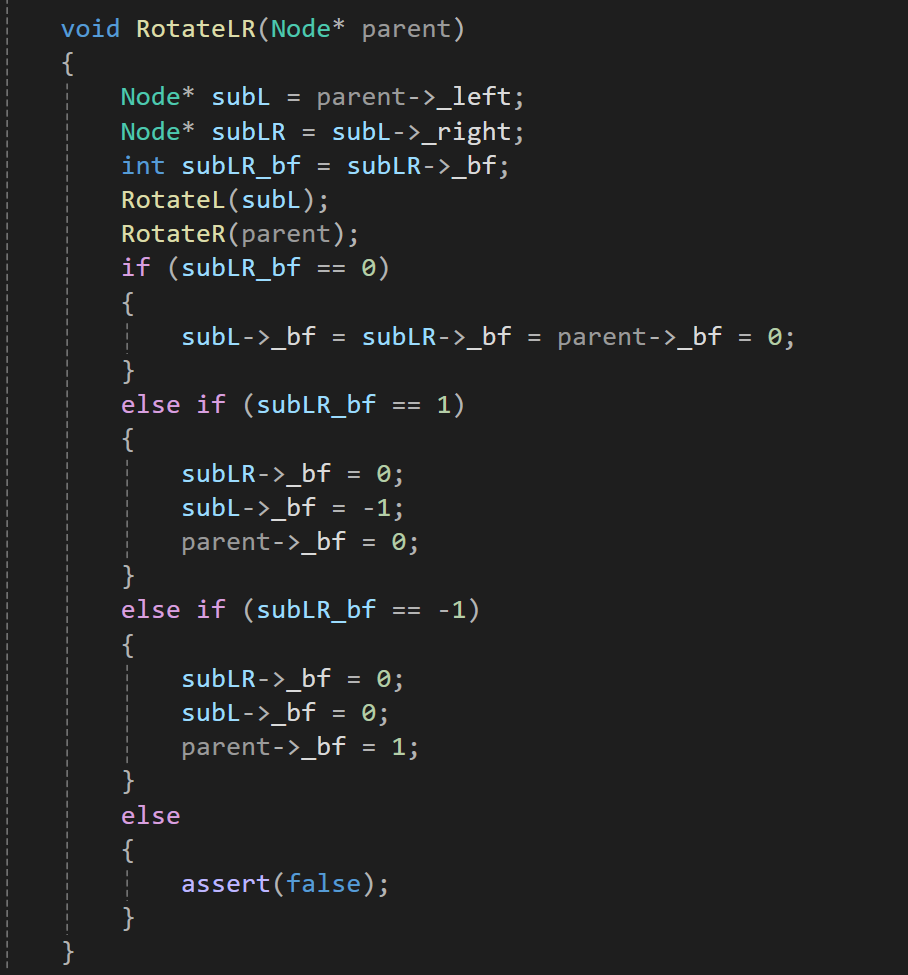
左右双旋细节:
在b的左子树进行插入新的结点
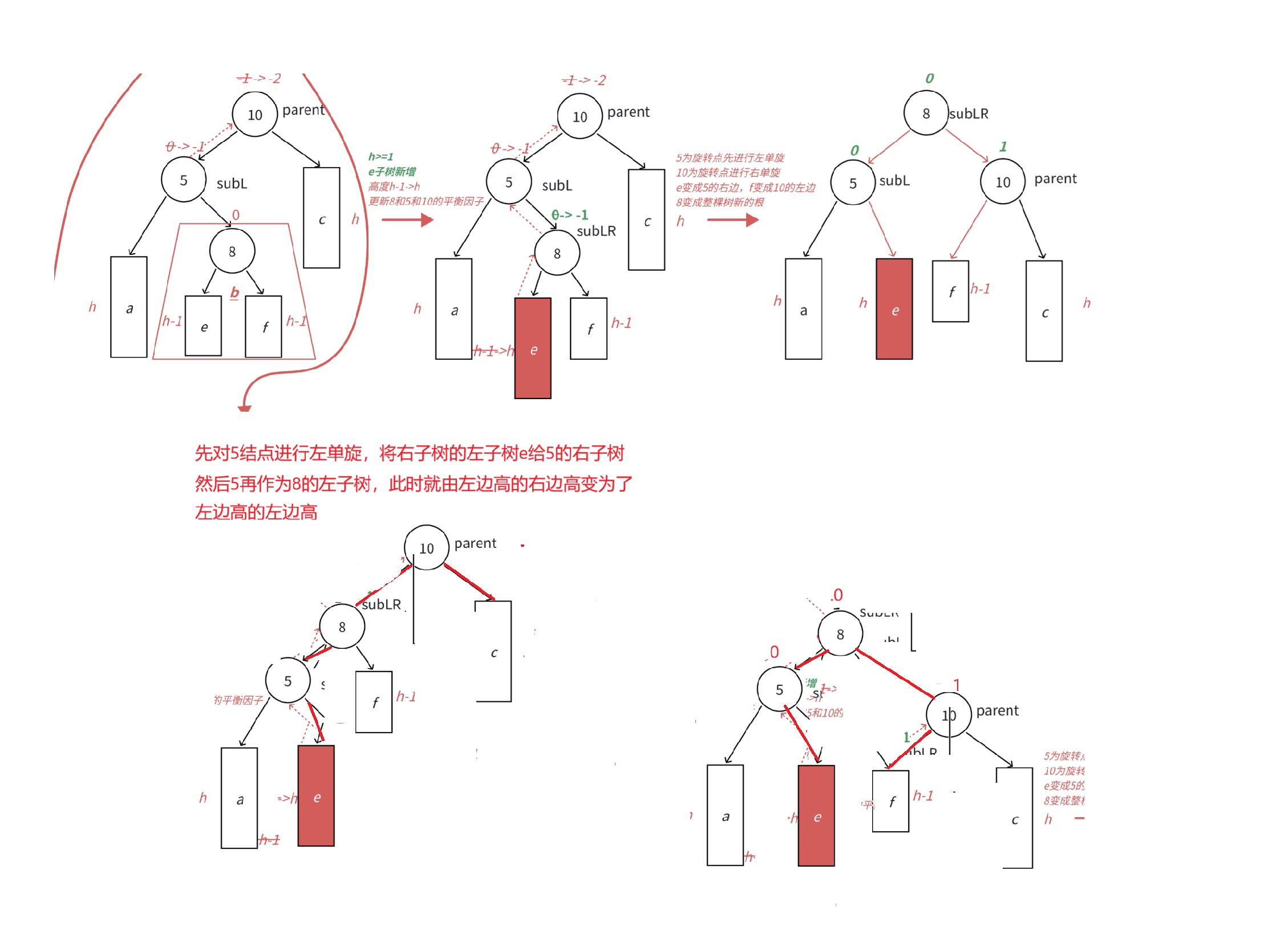
此时subLR的平衡因子为0,subL的平衡因子为0,parent的平衡因子为1
在b的右子树进行插入结点
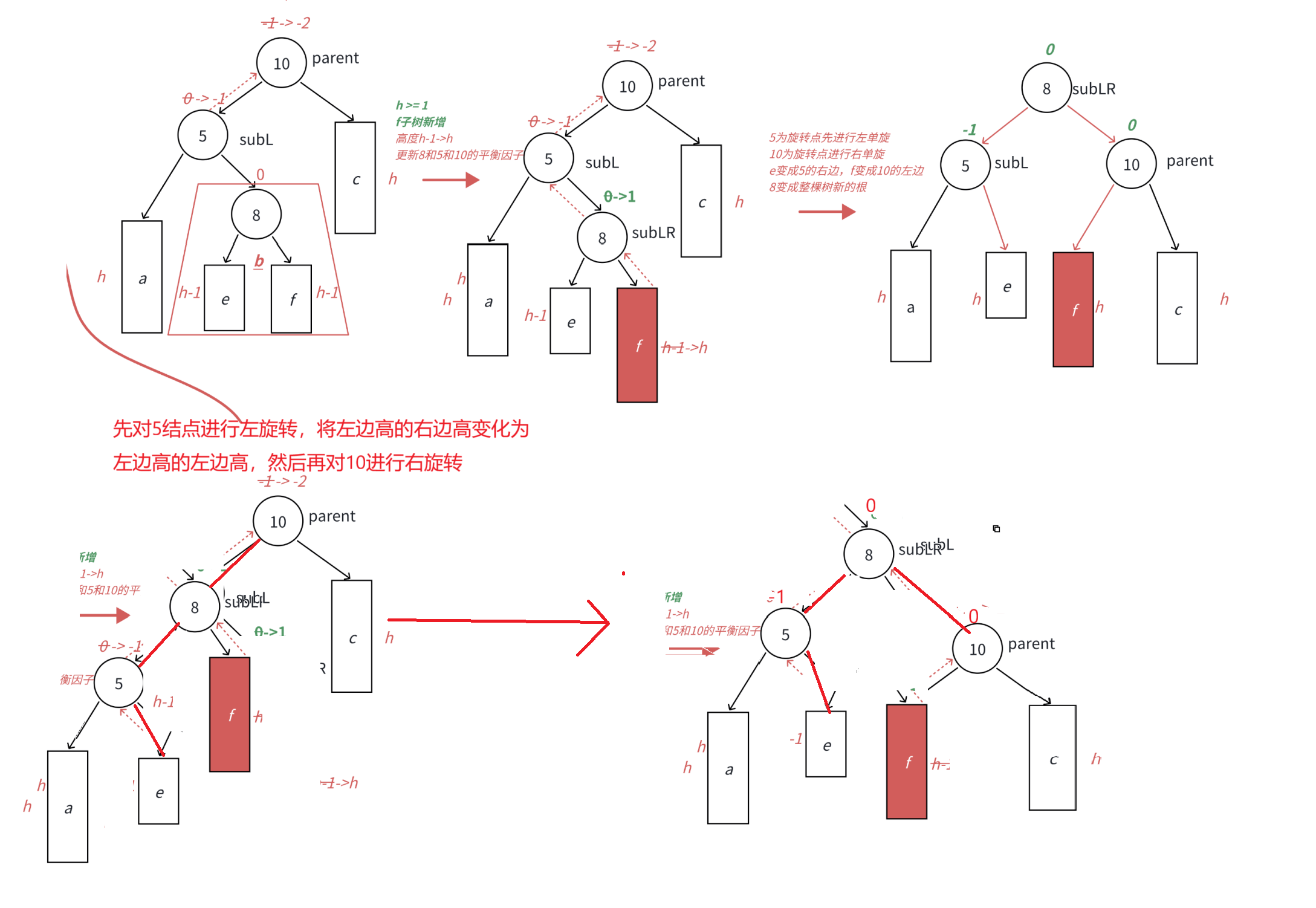
此时subRL的平衡因子为0,subL的平衡因子为-1,parent的平衡因子为0
当h == 0时,也就是b就为新增结点时
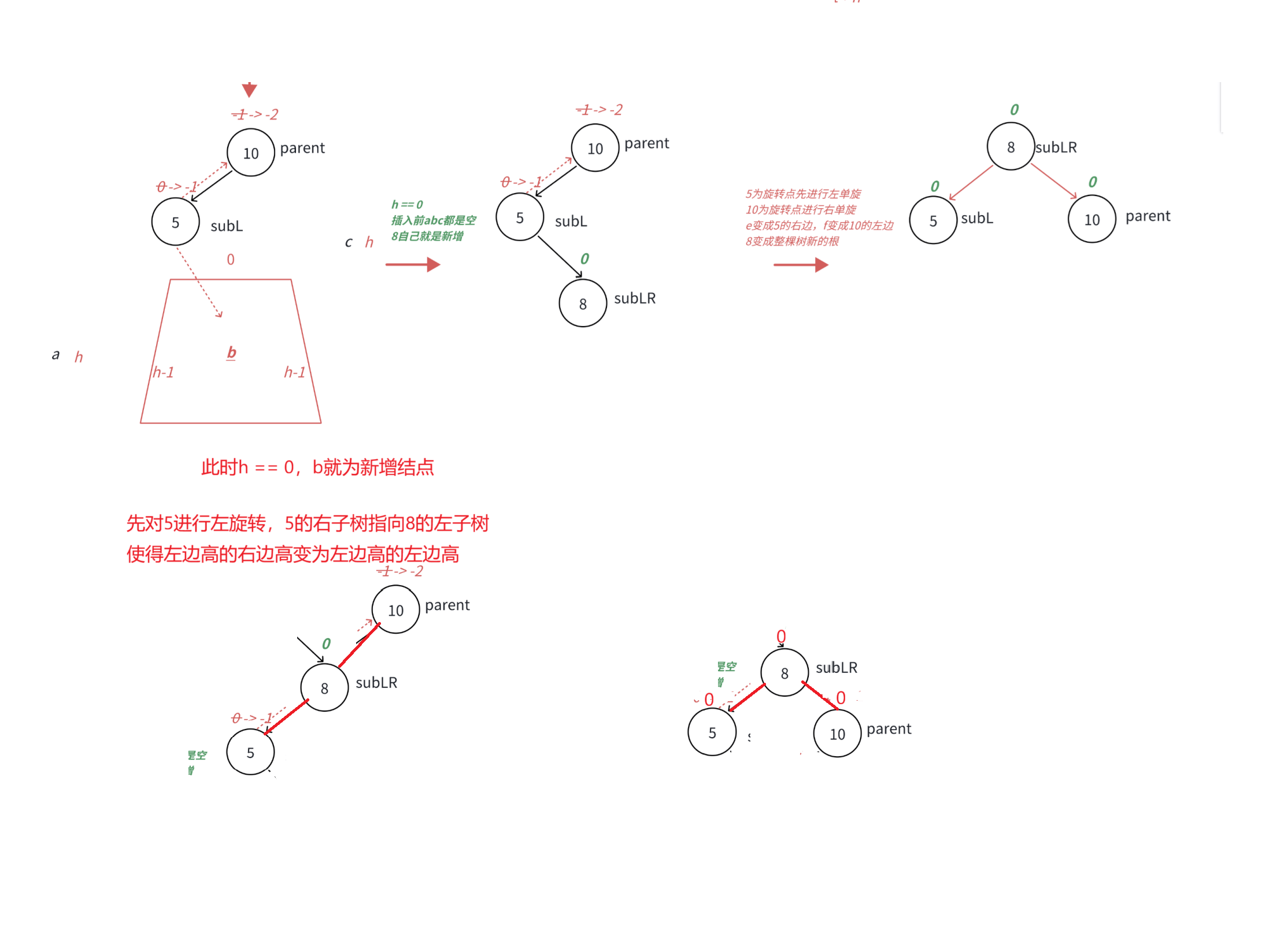
此时subRL,subR,parent的平衡因子皆为0
通过上述可以发现:
随着新增结点的位置不同,那么subRL,subR,parent的平衡因子都不一致
通过观察可以发现subLR的平衡因子决定了,旋转之后subRL,subR,parent的
平衡因子
双旋完毕后,左右子树的高度皆为h + 1,并且整体树的高度和插入前的高度一致
都为h + 2
d.代码实现
(4)右左双旋
当该结点的平衡因子为2时并且右子树的平衡因子为-1时,右高左高,采用右左双旋
a.该结点更新平衡因子之后为2,表明该结点在更新平衡因子之前为1,左右子树高度差为1
那么想要使得在右子树插入新的结点使得该结点的平衡因子更新为2,那么左子树的高度为
h,右子树的左右子树的高度为h
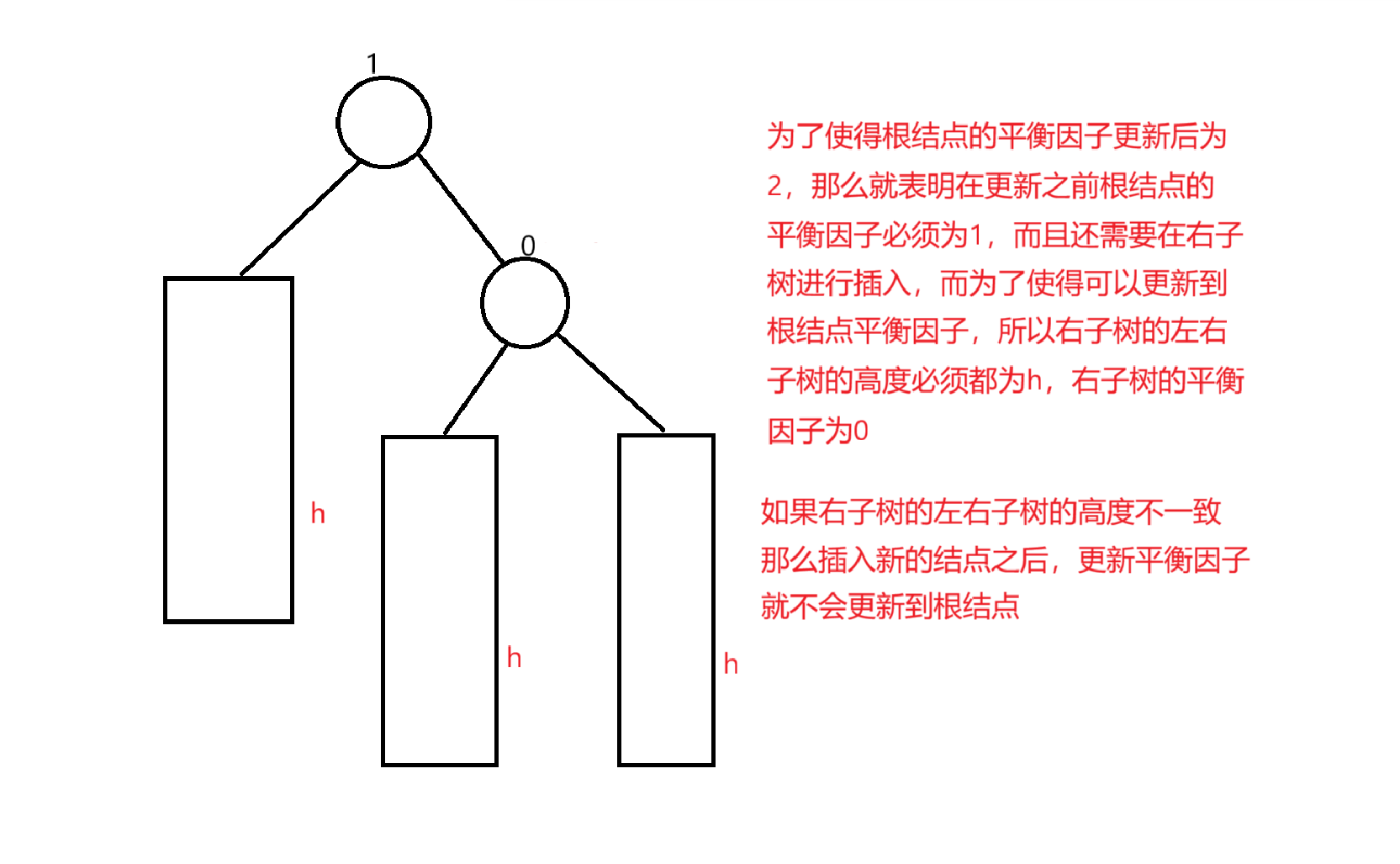
b.为了使得插入新结点之后根结点的平衡因子为2,右子树根节点的平衡因子为-1
那么就需要在右子树的左子树中进行插入,如果此时使用左单旋,会使得右边高
的左边高变化为左边高的右边高,必须使用双旋来解决问题
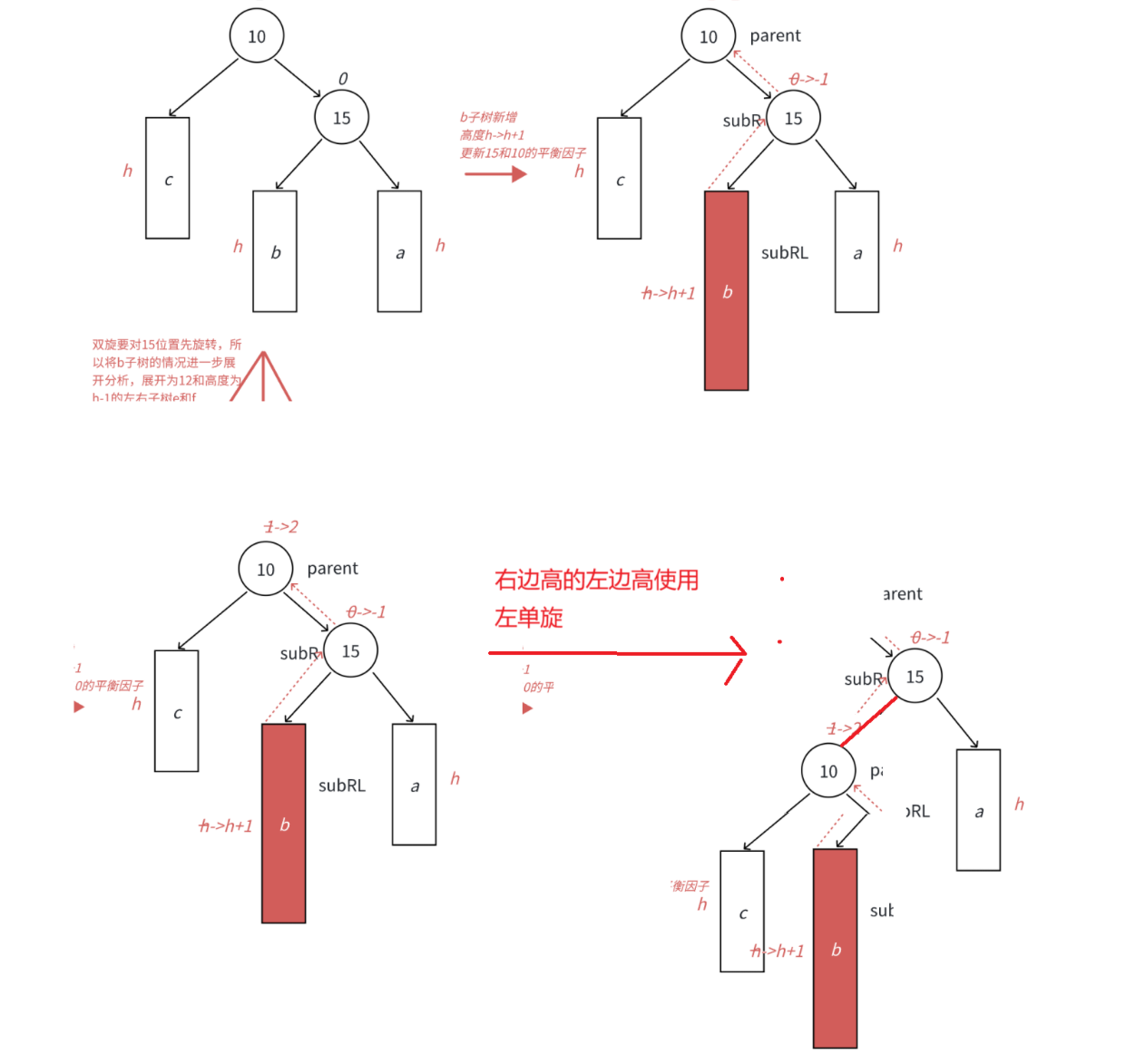
c.右左双旋本质上是使用两次单旋
逻辑上是:右边高的左边高不会进行修正,但是右边高的右边高会啊使用左单旋
首先对右子树的根节点进行一次右旋转,使得右边高的左边高变为右边高的右边高
然后再对根结点进行左旋转
以下图为例:
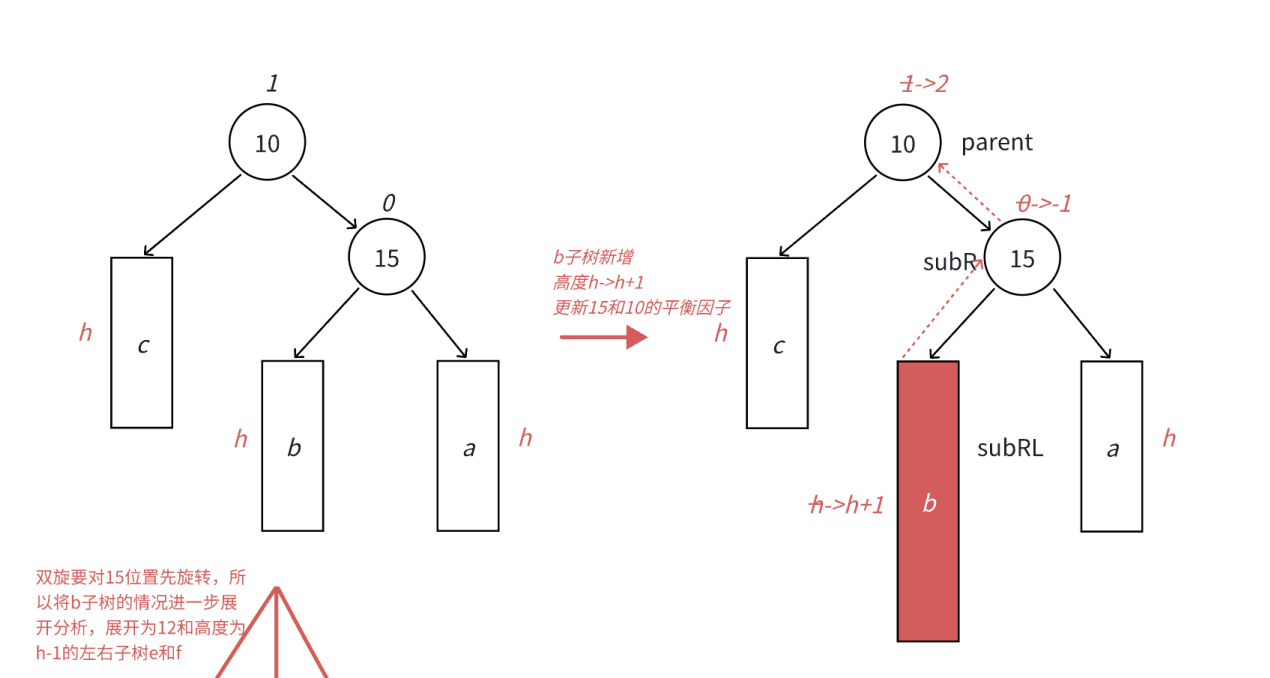
首先对15结点进行右旋转,将b的右子树作为15的左子树,然后15作为b的右子树
然后再对10进行左旋转,将b的左子树作为10的右子树,然后10作为b的左子树
此时双旋就谈论到了b的左子树和右子树,所以b必须展开讨论
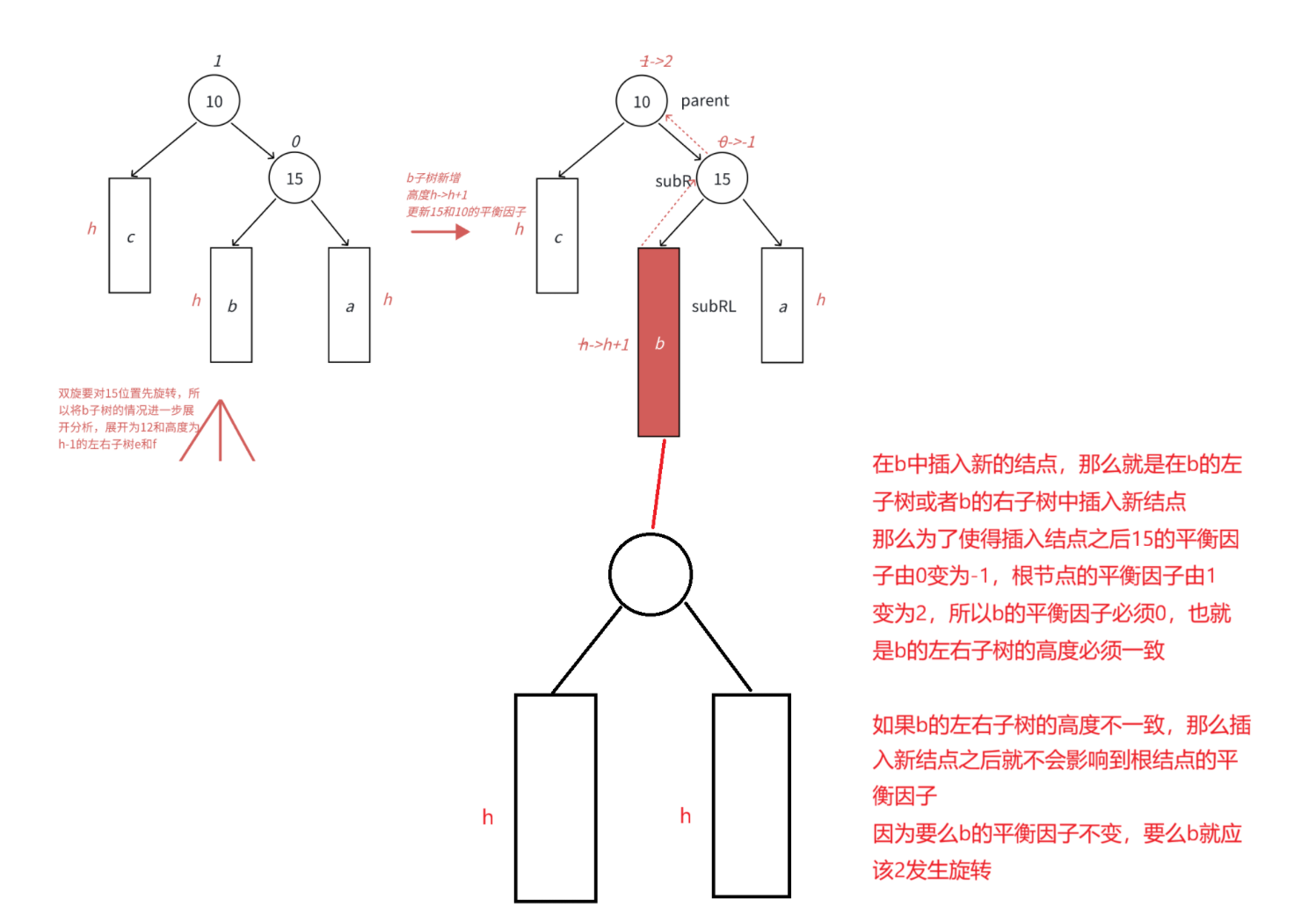
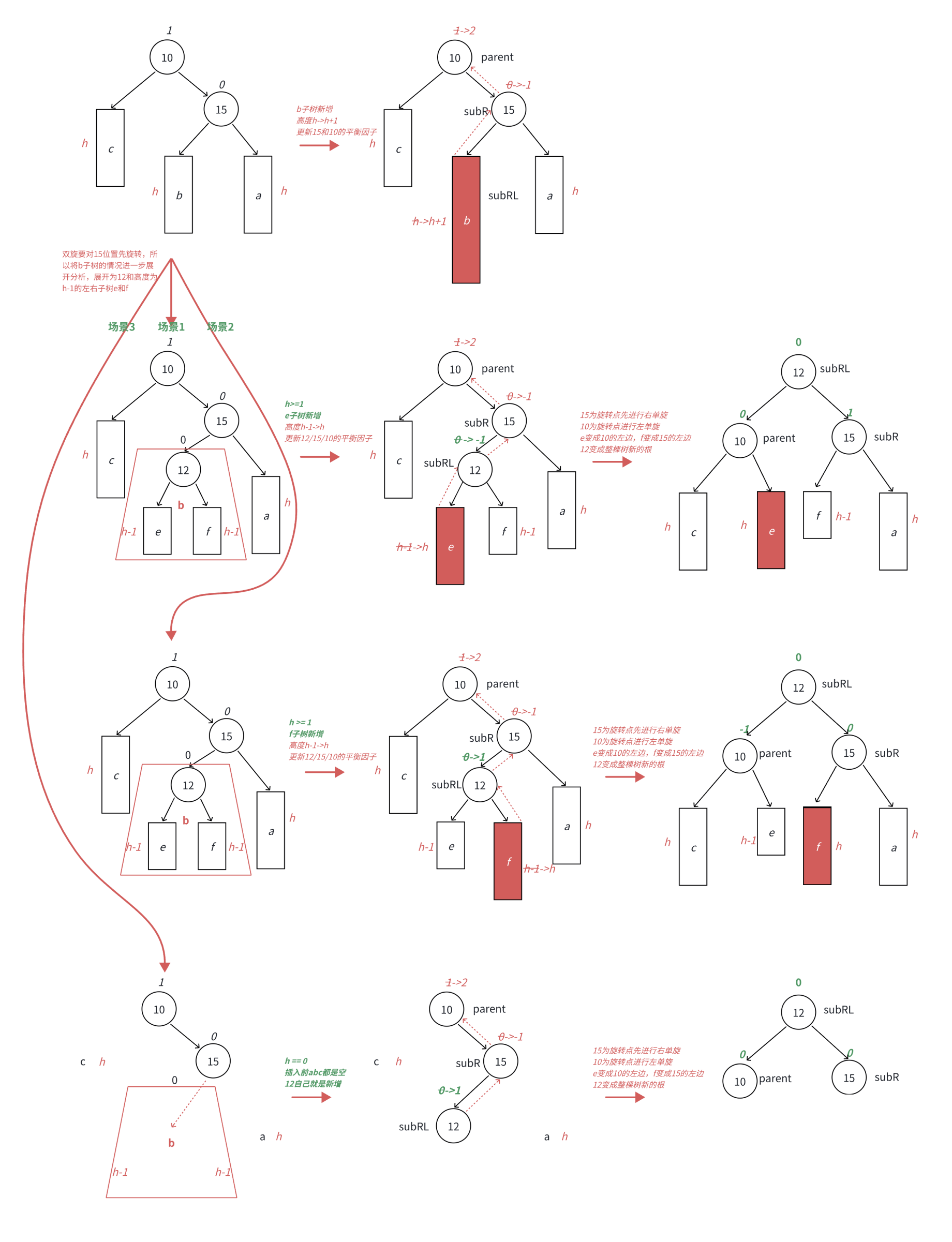
右左旋转细节:
在b的左子树中插入新的结点
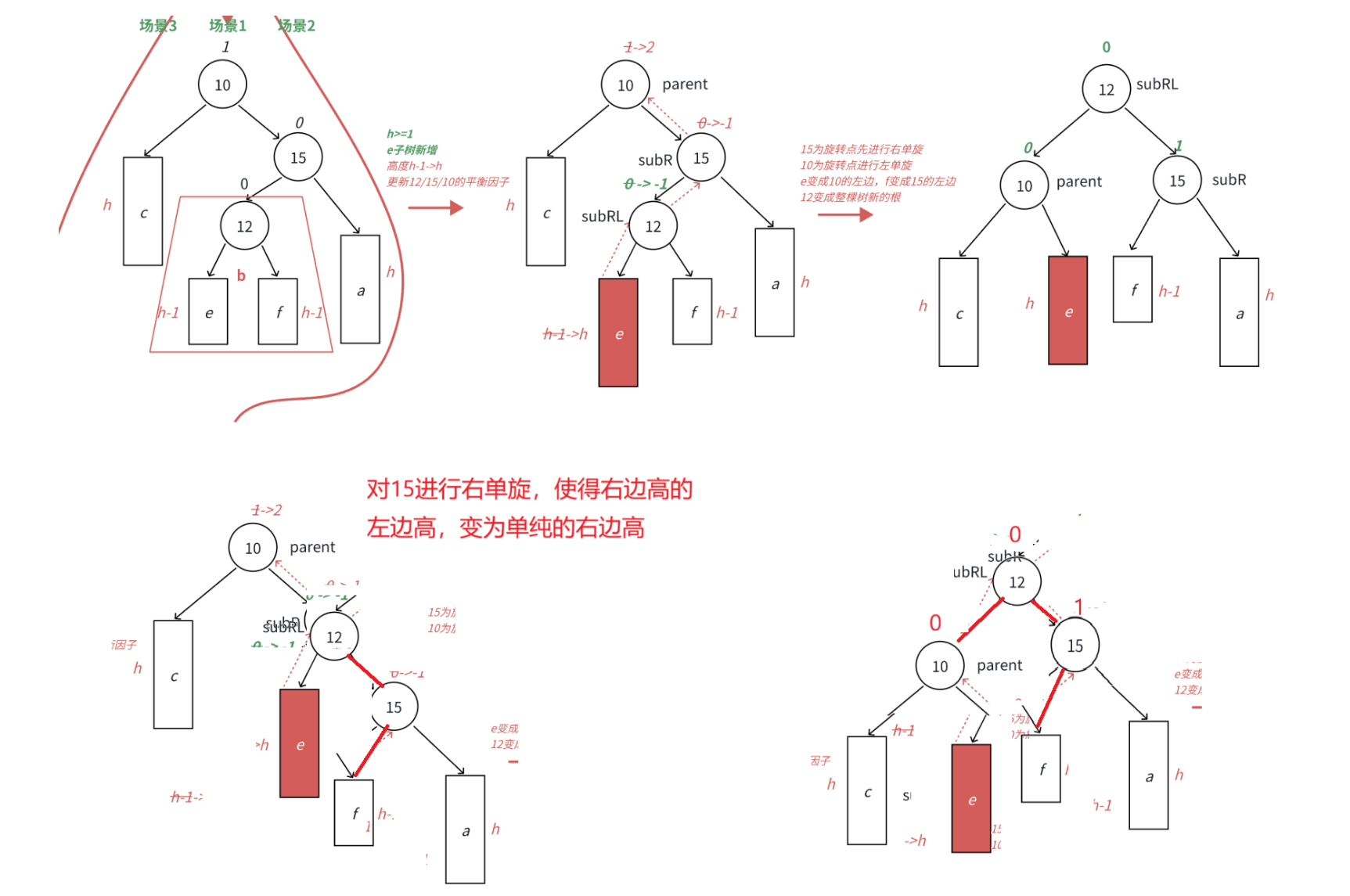
此时subRL的平衡因子为0,subR的平衡因子为1,parent的平衡因子为0
在b的右子树中插入新的结点
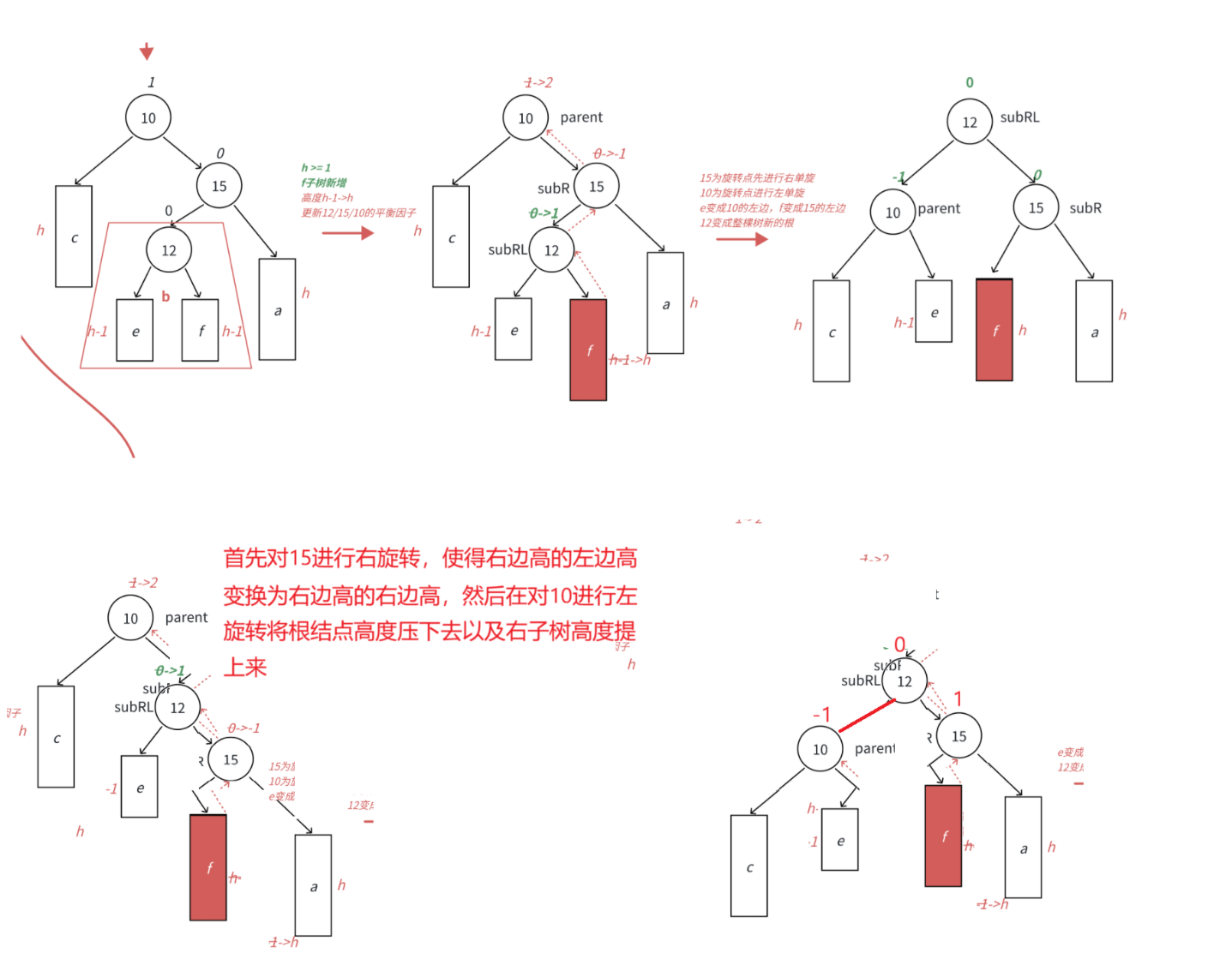
此时subRL的平衡因子为0,subR的平衡因子为0,parent的平衡因子为-1
当b就是新增结点时,也就是高度h == 0
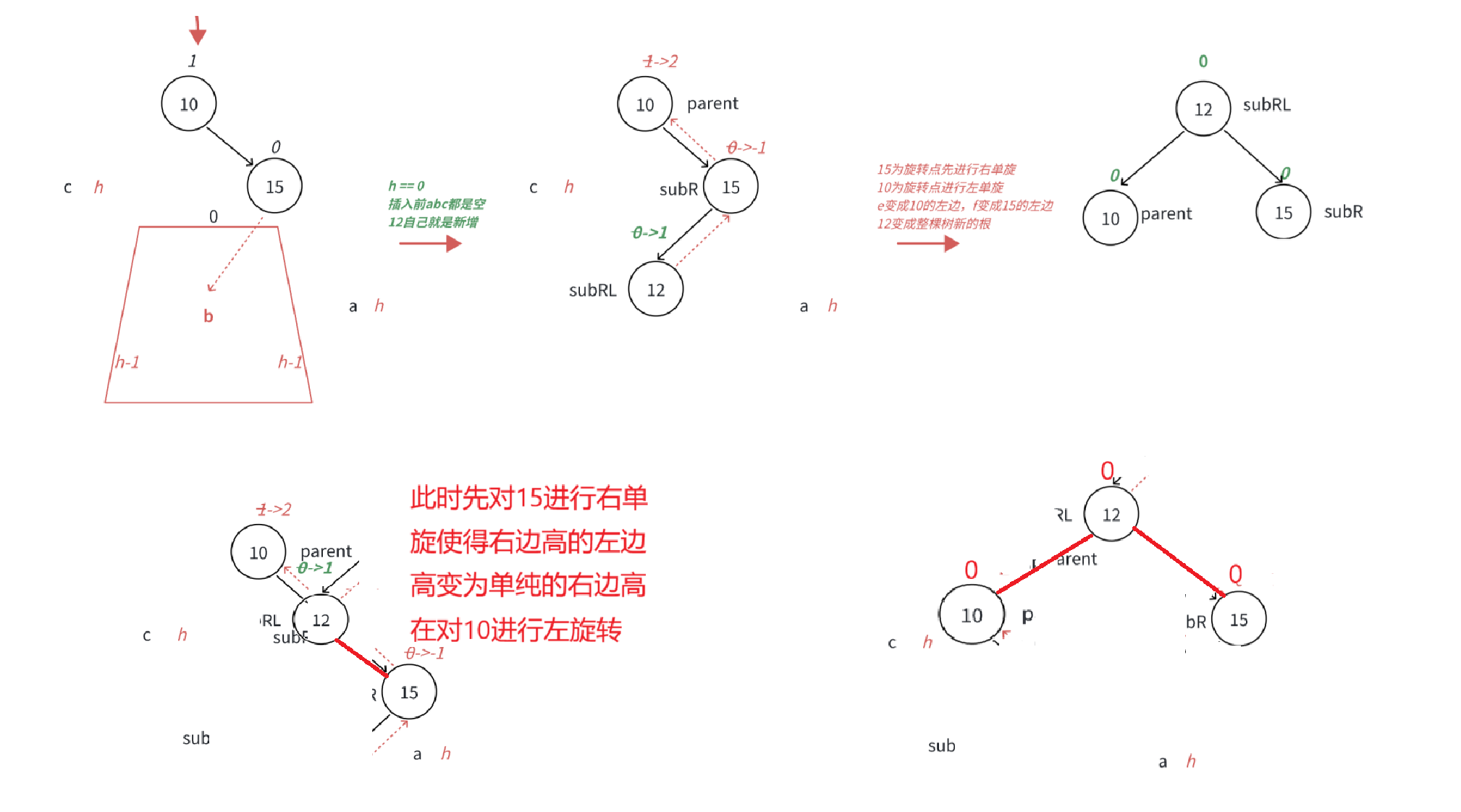
此时subRL,subR,parent的平衡因子皆为0
通过上述可以发现:
随着新增结点的位置不同,subRL,subR,parent旋转过后的平衡因子都不一样
通过观察可以发现subRL的平衡因子决定了,旋转之后subRL,subR,parent的
平衡因子
并且旋转过后左右子树的高度皆为h + 1,整颗树的高度和插入结点之前的高度也一致
皆为h + 2
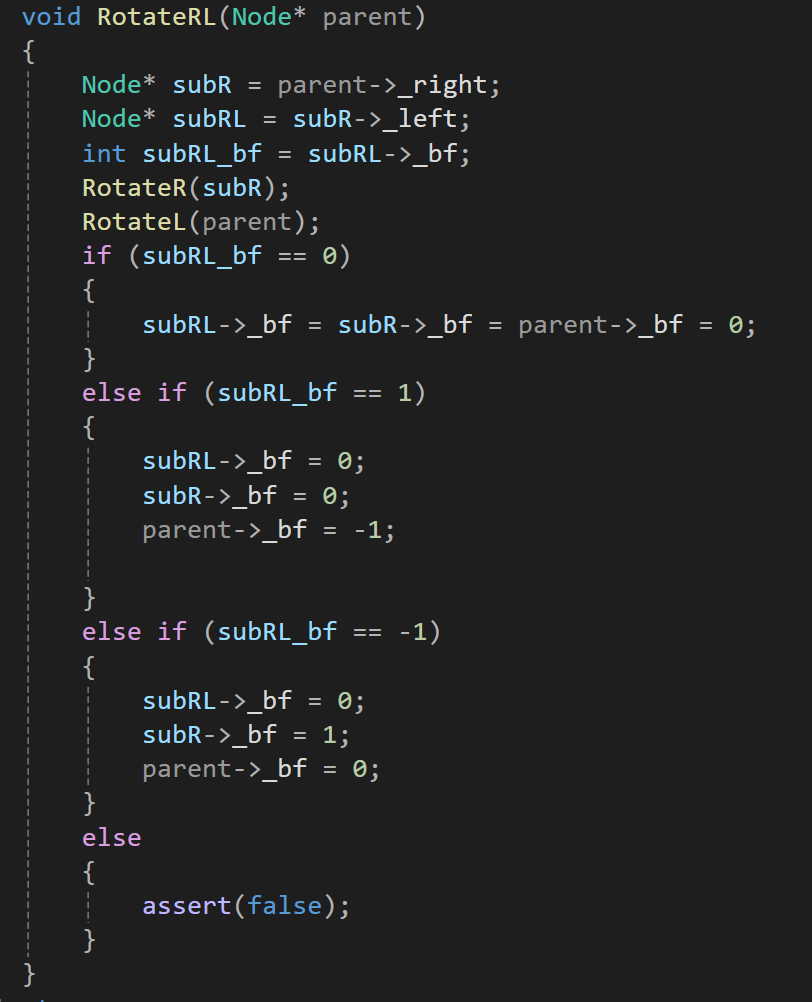
d.代码实现
6.完整代码

