双指针算法_移动零

移动零

题目链接：移动零

题目解析：

例如：[0，1，0，3，12]，在不复制数组的情况下，对它进行操作，结果如下：
[1，3，12，0，0]，可以看到，满足了题目的两个要求：

1. 0 都在数组的末尾
2. 非零元素的相对顺序，是有序的，由小到大

讲解算法原理

类似于这种对数组内容进行操作的题目，可以理解为 数组划分 或 数组分块 问题。

数组划分问题的特点：
给定一个数组，根据某种规则，将数组的内容，划分为若干个区间。

例如这道 移动零 的题目：
给定一个数组：[0，1，0，3，12]
规则：非零元素移动到数组的左边，0 移动到数组的右边（末尾），同时非零元素的相对顺序得保持。

解决这类题目，有一个很经典的算法：双指针算法

双指针算法的介绍：

这里的指针，并 不是 C语言 当中的指针。

这里的指针，指的是 数组下标 来作为指针。因为数组里面，有个很好的特性，我们可以通过数组的下标，来索引（寻找）到数组的元素。

（对于本题）双指针算法的效果：

首先，先定义两个 int 类型的整数，作为指针。

变量名是自定义的，这里使用 dest 和 cur 。
dest => destination 终点，目的地
cur => current 最近的

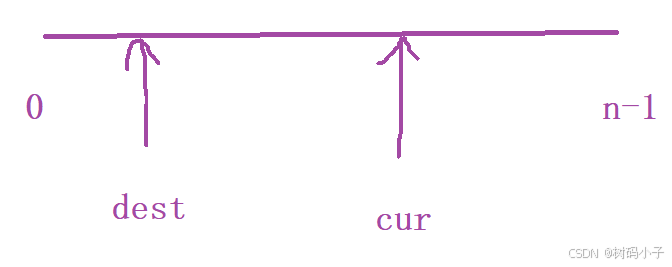
两个指针的作用：
cur：从左往右扫描数组，遍历数组
dest：已处理的区间内，非零元素的最后一个位置（作为一个分割线）

画一个图来展示这两个指针的作用：

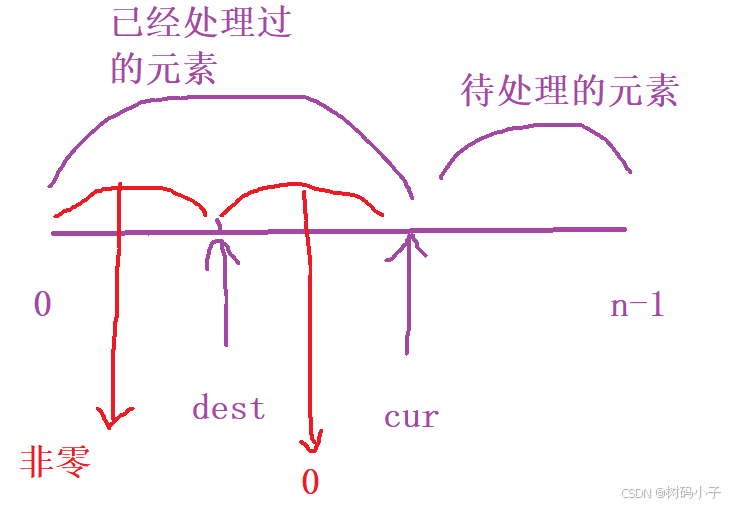
利用这两个变量，将这个数组的内容划分为三个区间：
第一个：[ 0，dest ] ，已经处理过的区间，里面全都是 非零元素
第二个：[ dest+1，cur-1 ] ，已经处理过的区间，里面全都是 0
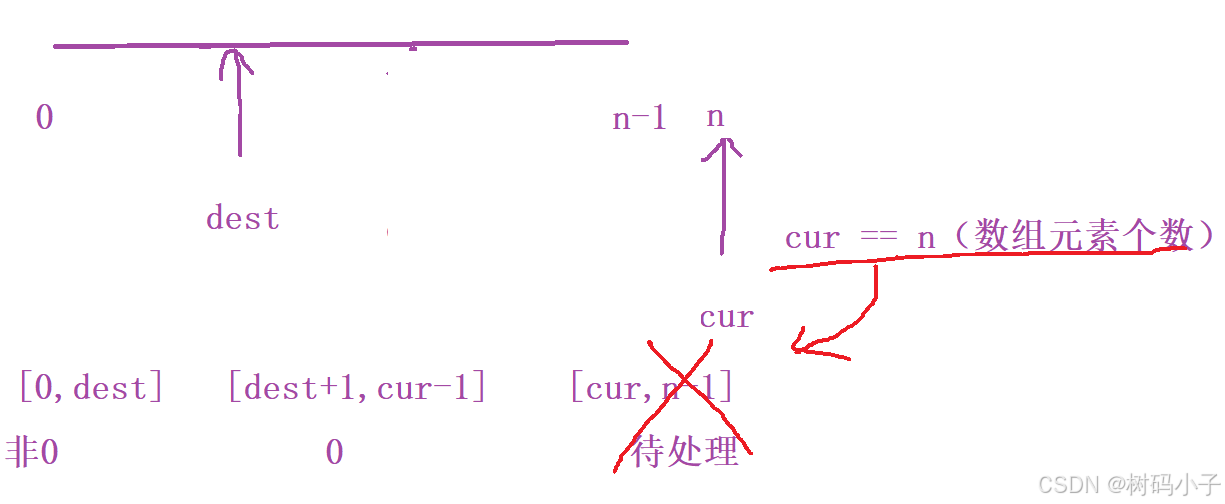
第三个：[ cur，n-1 ] ，cur当前所指向的元素，是没有被处理过的元素，n-1 是因为数组的下标是从 0下标 开始的，下标的最大值为 数组元素个数（n）-1 ，这个区间表示的是待处理的元素

当 dest 和 cur 从左向右走的过程中，三个一直保持这样的性质的话，当 cur 这个指针 等于 n 时，也就是把整个数组扫描过一遍之后（cur == n），待处理的区间的没有了。

解题分析：

对这两个指针进行初始化：
cur：初始化为 0，因为它是要从左到右遍历整一个数组的。
dest：由于刚开始进行数组扫描的时候，是没有 非零元素 的，所以，初始化为 -1。

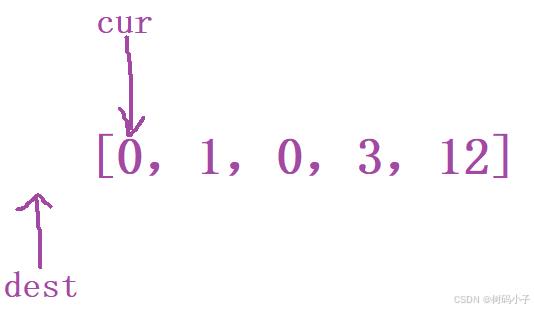
算法演示：

解题代码：

//这是力扣提交的代码部分
class Solution {public void moveZeroes(int[] nums) {
//        刚开始时没有非零元素的，dest初始化为 -1int dest = -1;for(int cur = 0;cur < nums.length;cur++) {
//            由于遇到 0 ，不做处理，仅 cur++
//            而for循环结束的最后，就会进行 cur++
//            所以，仅需要处理遇到 非零元素 的情况if(nums[cur] != 0) {dest++;int tmp = nums[cur];nums[cur] = nums[dest];nums[dest] = tmp;}}}
}