预测赢家-区间dp

486. 预测赢家 - 力扣（LeetCode）

Solution

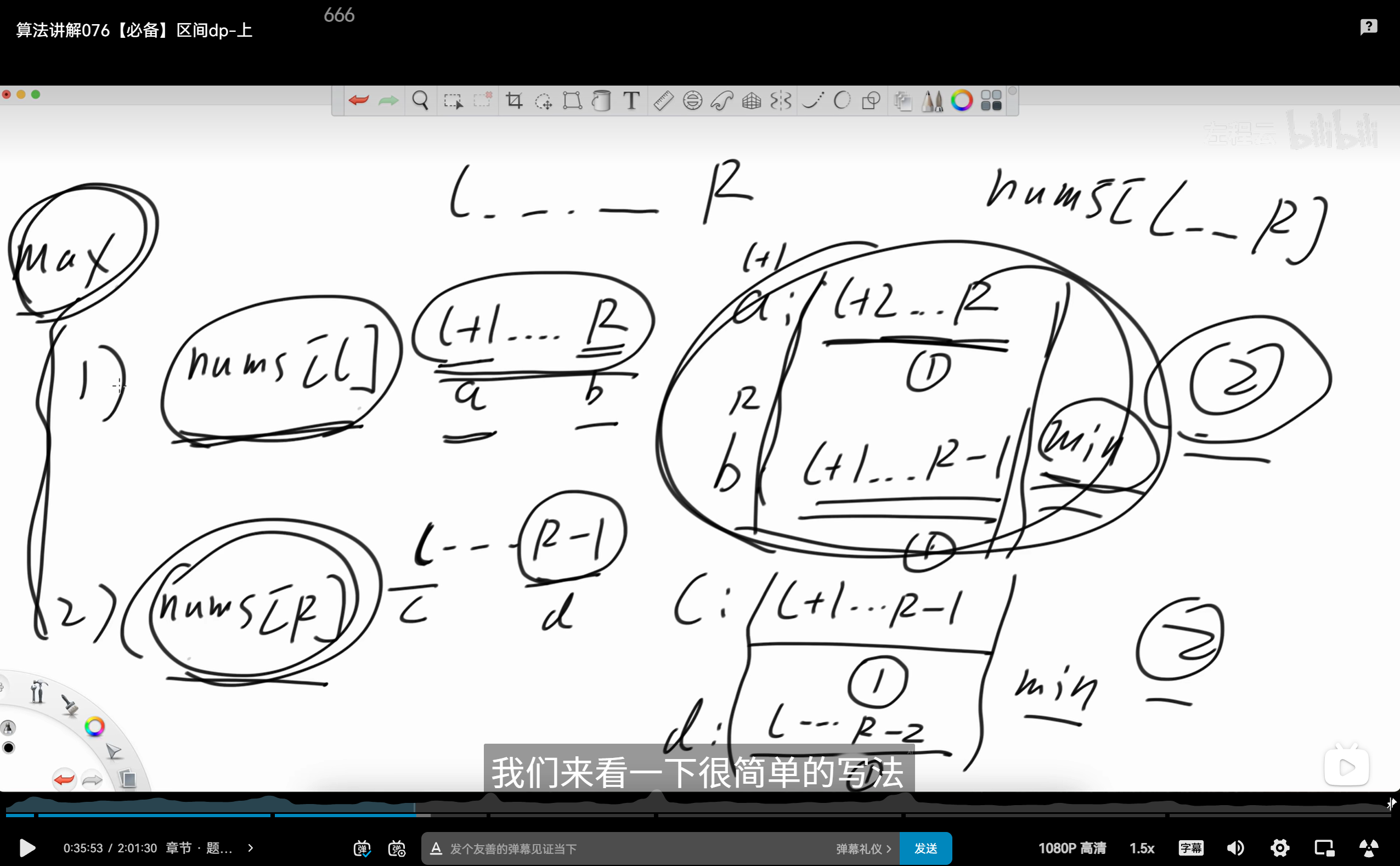
这题的关键在于理解这个最佳策略，两边都是绝顶聪明的，都会使自己的策略最优。

#include<iostream>
#include<vector>
using namespace std;class Solution {
public:bool predictTheWinner(vector<int>& nums) {int n = nums.size();vector<vector<int>>dp(n + 1, vector<int>(n + 1, -1));int sum = 0;for (int num : nums)sum += num;int s1 = f2(nums, 0, n - 1, dp);int s2 = sum - s1;return s1 >= s2;}//递归做法int f1(vector<int>& nums, int l, int r) {if (l == r) return nums[l];if (l + 1 == r) return max(nums[l], nums[r]);int p1 = nums[l] + min(f1(nums, l + 2, r), f1(nums, l + 1, r - 1));int p2 = nums[r] + min(f1(nums, l, r - 2), f1(nums, l + 1, r - 1));return max(p1, p2);}//带缓存表的递归int f2(vector<int>& nums, int l, int r, vector<vector<int>>& dp) {if (dp[l][r] != -1) return dp[l][r];if (l == r) return nums[l];if (l + 1 == r) return max(nums[l], nums[r]);int p1 = nums[l] + min(f2(nums, l + 2, r, dp), f2(nums, l + 1, r - 1, dp));int p2 = nums[r] + min(f2(nums, l, r - 2, dp), f2(nums, l + 1, r - 1, dp));dp[l][r] = max(p1, p2);return dp[l][r];}
};int main() {return 0;
}