当前位置：首页 > news >正文

2023年EAAI SCI1区TOP，基于差分进化的自适应圆柱矢量粒子群优化无人机路径规划，深度解析+性能实测

news 2025/9/12 5:28:29

1.摘要

粒子群优化（PSO）算法在无人机（UAV）路径规划中具有潜力，但在复杂多威胁的环境中，传统PSO算法容易陷入局部最优。为提高算法在复杂环境中的性能，本文提出了具备自适应调整参数、圆柱向量和差分进化算子的粒子群算法（ACVDEPSO）。在ACVDEPSO中，粒子的速度被转换为圆柱向量，以便更有效地进行路径搜索。同时，算法的参数根据粒子的时间和适应度自动调整。此外，差分进化算子的引入有效减少了局部最优的发生概率，加速了算法的收敛速度。

2.数学模型

常见UAV模型，略~

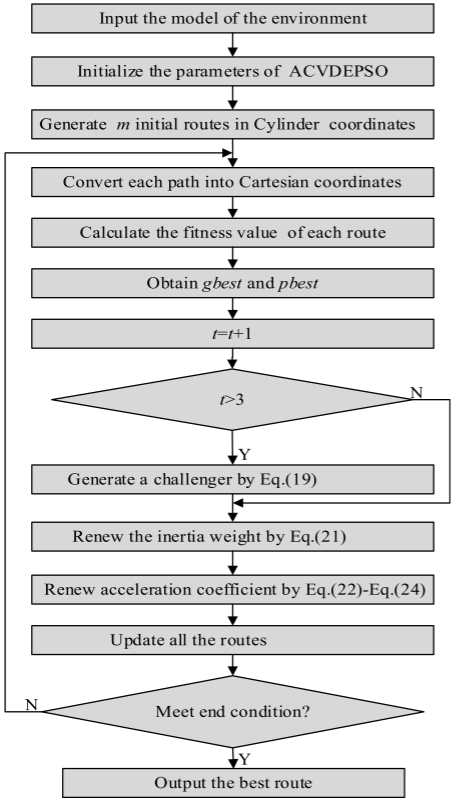
3.改进粒子群算法

为提高粒子群优化（PSO）算法的效率，本文提出了一种自适应参数策略，结合粒子适应度、个体信息和演化时间，同时引入差分进化策略。在无人机路径规划中，采用圆柱坐标替代笛卡尔坐标来表示航路点：
$Pi=(ri1,θi1,zi1,ri2,θi2,zi2,...,riN,θiN,ziN)P_{i}=(r_{i1},\theta_{i1},z_{i1},r_{i2},\theta_{i2},z_{i2},...,r_{iN},\theta_{iN},z_{iN})$

将每个粒子视为一条飞行路径，相应的速度可用增量矢量表示:
$ΔPi=(Δri1,Δθi1,Δzi1,Δri2,Δθi2,Δzi2,…,ΔriD,ΔθiD,ΔziD)\Delta P_i=(\Delta r_{i1},\Delta\theta_{i1},\Delta z_{i1},\Delta r_{i2},\Delta\theta_{i2},\Delta z_{i2},\ldots,\Delta r_{iD},\Delta\theta_{iD},\Delta z_{iD})$

每个粒子的更新方程:
${Δqijk+1=ωΔqijk+c1r1(pijk−qijk)+c2r2(gjk−qijk)qijk+1=qijk+Δqijk+1,(i=1,2,…,m;j=1,2,…,N)\begin{cases} \Delta q_{ij}^{k+1} = \omega \Delta q_{ij}^{k} + c_1 r_1 (p_{ij}^{k} - q_{ij}^{k}) + c_2 r_2 (g_{j}^{k} - q_{ij}^{k}) \\ q_{ij}^{k+1} = q_{ij}^{k} + \Delta q_{ij}^{k+1}, \quad (i = 1, 2, \dots, m; j = 1, 2, \dots, N) \end{cases}$

将航路点 $W$ 投影到 Oxy 平面上，可以将圆柱坐标转换为笛卡尔坐标：
${xj=xj−1+rjcos⁡θijyj=yj−1+rjsin⁡θijzj=zj−1+Δzj\begin{cases} x_j=x_{j-1}+r_j\cos\theta_{ij} \\ y_j=y_{j-1}+r_j\sin\theta_{ij} \\ z_j=z_{j-1}+\Delta z_j & \end{cases}$

圆柱坐标 $r$ 和 $θ\theta$ 范围

为了加速搜索速度并使得生成的航路点均匀分布， $r$ 范围：
$0≤r≤2∣∣G−S∣∣N0\leq r\leq\frac{2||G-S||}{N}$

$θ\theta$ 范围：
$θmin⁡=arctan⁡(yG−ySxG−xS)−θr\theta_{\min}=\arctan\left(\frac{y_G-y_S}{x_G-x_S}\right)-\theta_r$

$θmax⁡=arctan⁡(yG−ySxG−xS)+θr\theta_{\max}=\arctan\left(\frac{y_G-y_S}{x_G-x_S}\right)+\theta_r$

引入差分进化算子，根据上一代的全局最优解生成新解：
$qjk+1=gbjr1+rand(0,1)⋅(gbjr2−gbjr3),(k≥3,j=1,2,…,N)q_{j}^{k+1}=gb_{j}^{r_{1}}+rand(0,1)\cdot(gb_{j}^{r_{2}}-gb_{j}^{r_{3}}),(k\geq3,j=1,2,\ldots,N)$

The flow of the ACVDEPSO algorithm

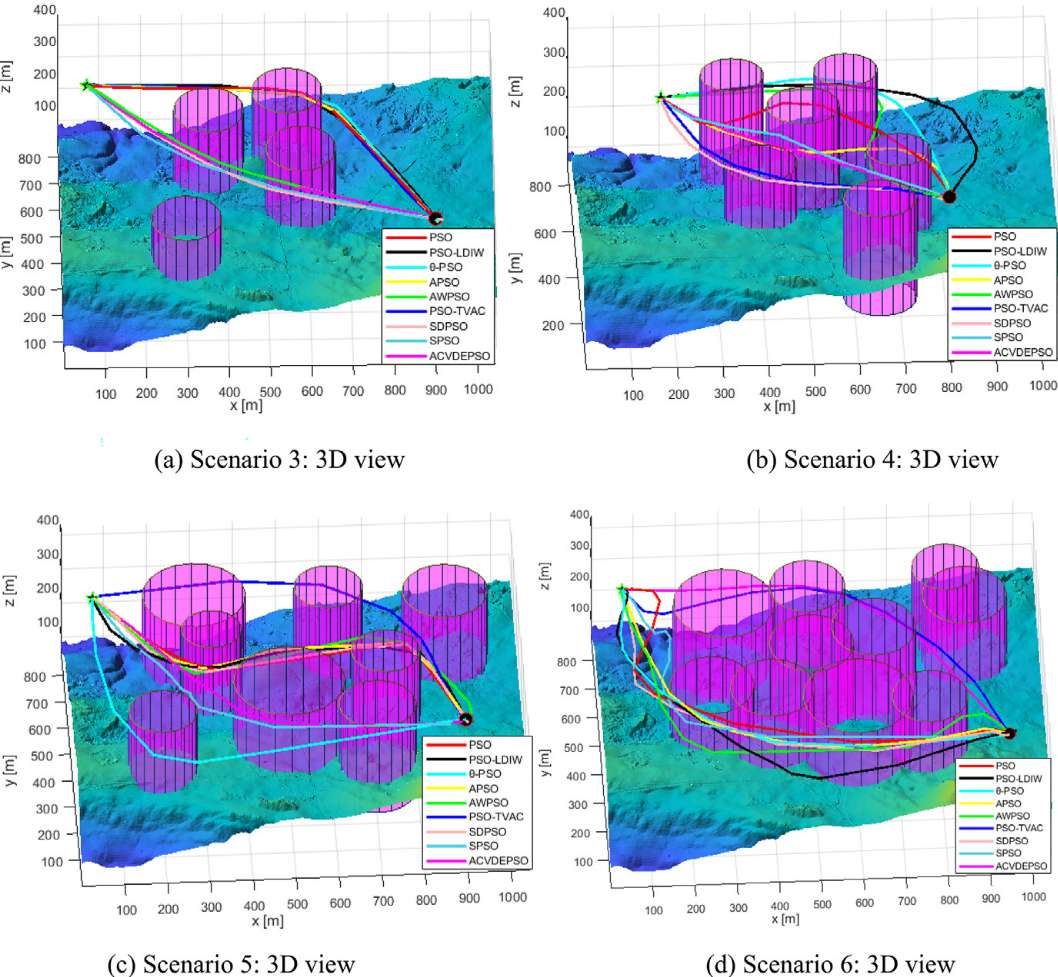
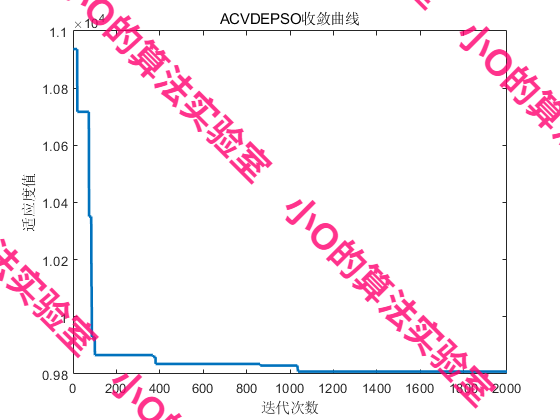
4.结果展示

论文仿真

5.参考文献

[1] Huang C, Zhou X, Ran X, et al. Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning[J]. Engineering Applications of Artificial Intelligence, 2023, 121: 105942.