【leetcode】63. 不同路径 II

题目

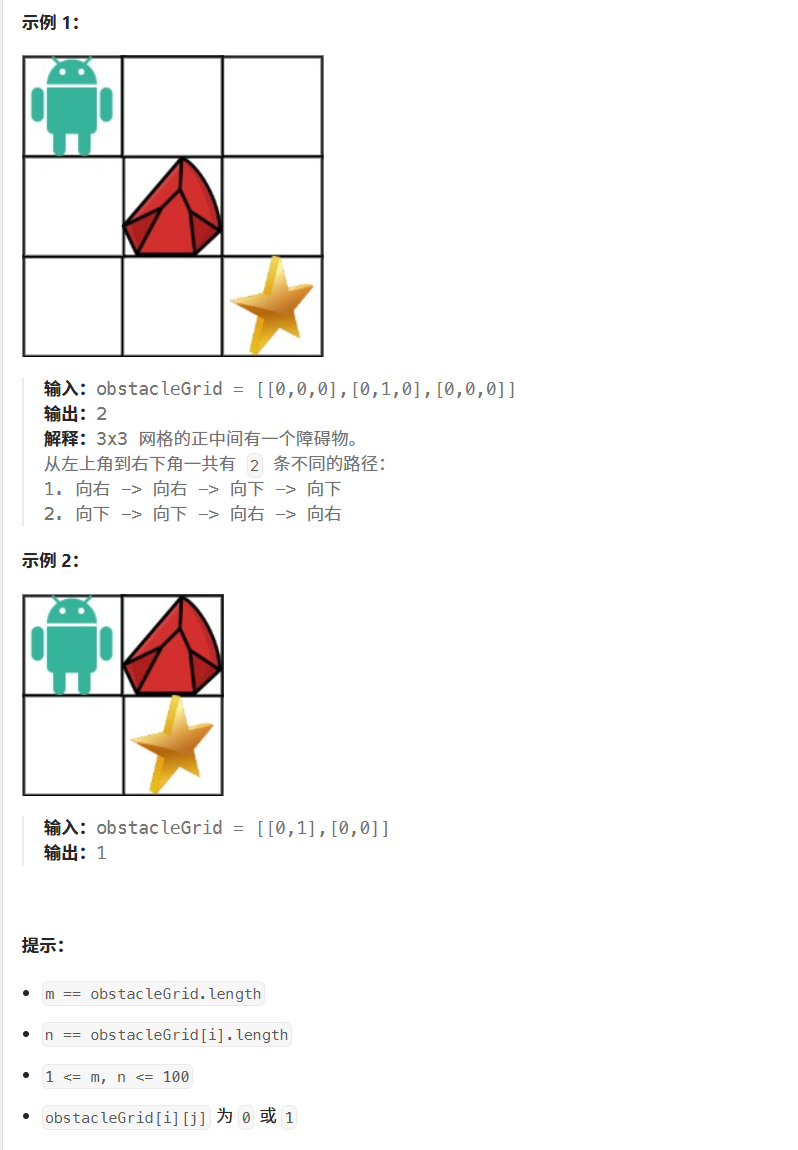
63. 不同路径 II

给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。

返回机器人能够到达右下角的不同路径数量。

测试用例保证答案小于等于 2 * 109。

题解

1. 在初始位置或者结束位置有障碍物，则返回0
2. 在第一行或者第一列上移动，只有一种方式，且遇到障碍物，之后的路径与之前一样的状态
3. obstacleGrid[i][j]有障碍物，dp[i][j] = 0
4. 若没有障碍物，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

class Solution(object):def uniquePathsWithObstacles(self, obstacleGrid):""":type obstacleGrid: List[List[int]]:rtype: int"""if obstacleGrid[0][0] == 1 or obstacleGrid[-1][-1] == 1:return 0m = len(obstacleGrid)n = len(obstacleGrid[0])dp = [[0] * n for _ in range(m)]dp[0][0] = 1for i in range(1, m):if obstacleGrid[i][0] == 0:dp[i][0] = dp[i - 1][0]else:dp[i][0] = 0for j in range(1, n):if obstacleGrid[0][j] == 0:dp[0][j] = dp[0][j - 1]else:dp[0][j] = 0for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:dp[i][j] = 0else:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[-1][-1]