【Python/Pytorch】-- 贝叶斯定理

文章目录

01 贝叶斯定理的理解

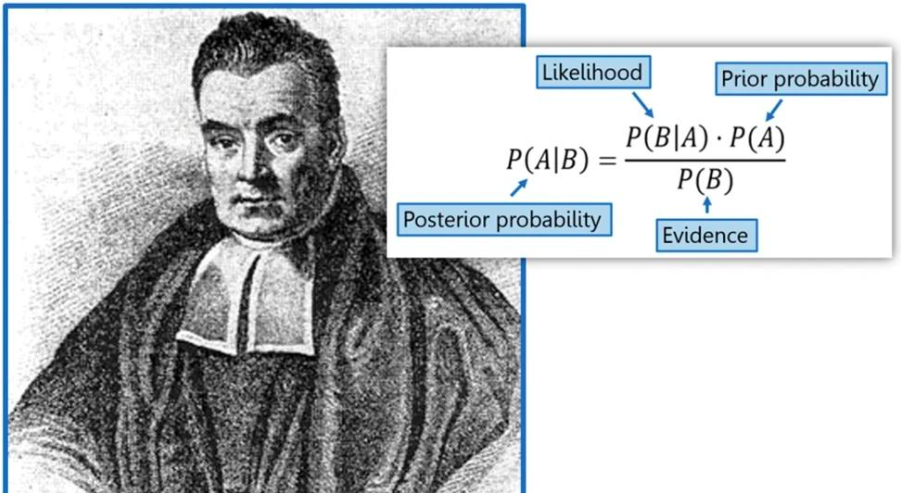
贝叶斯定理的基本公式：P(A|B)=P(B|A)*P(A) / P(B)
首先是如何理解这个公式？
在B事件发生的条件下，A发生的概率 P(A|B) = 在B事件发生的条件下，A和B同时发生的概率P(A∩B)；
同理，在A事件发生的条件下，B发生的概率 P(B|A) = 在A事件发生的条件下，A和B同时发生的概率P(A∩B)；
两个等式，即可推出贝叶斯定理：P(A|B)=P(B|A)*P(A) / P(B)

如果是连续变量，比如图像x、观测数据y，公式为：P(x|y)=P(y|x)*P(x) / P(y)
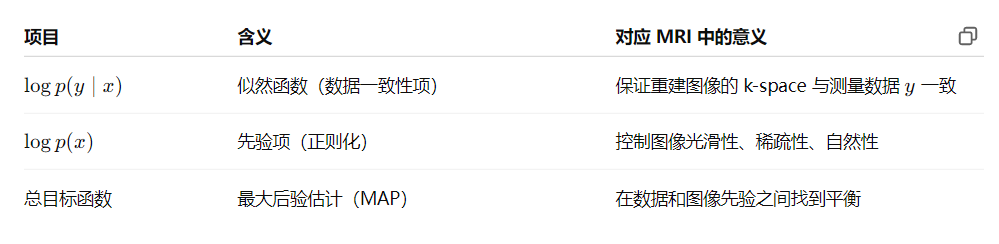
P(x|y) 后验概率（我们想求的）
P(y|x) 似然（生成观测数据的过程）
P(x) 先验（我们对图像的经验，平滑、低秩、稀疏）
P(y) 边际似然（归一化常数）

02 在MRI重建领域应用