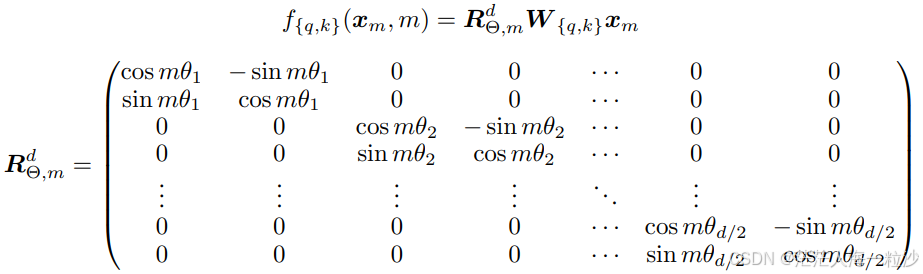大模型中的位置编码详解
在大语言模型(LLM, Large Language Model)中,位置编码(Positional Encoding, PE)是一项关键技术。由于 Transformer 架构本身并不具备序列顺序的建模能力,因此必须引入额外的位置信息,使模型能够区分输入序列中 token 的先后关系。
本文将介绍 三种常见的位置编码方式:绝对位置编码、相对位置编码、旋转位置编码(RoPE),并结合代码示例和可视化来说明它们的工作原理。
1. 为什么需要位置编码?
Transformer 的核心是自注意力机制(Self-Attention),其计算公式为:
![]()
这里 $Q, K, V$ 都是由输入序列映射得到的向量。如果没有位置编码,不同顺序的输入(如 "我爱你" vs "你爱我")在注意力层中会被视为同一组词袋,完全丧失序列信息。因此,需要为每个位置注入 唯一的位置信息。
2. 绝对位置编码
原理
绝对位置编码是最早在 Transformer 论文《Attention is All You Need》中提出的方法。它通过正弦和余弦函数生成一组固定向量,并将其加到输入 embedding 上。
公式:
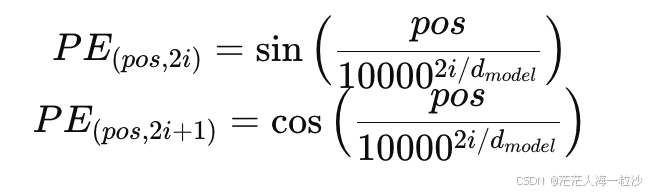
代码示例
import numpy as npdef sinusoidal_pos_encoding(seq_len, dim):position = np.arange(seq_len)[:, np.newaxis]div_term = np.exp(np.arange(0, dim, 2) * -(np.log(10000.0) / dim))pe = np.zeros((seq_len, dim))pe[:, 0::2] = np.sin(position * div_term)pe[:, 1::2] = np.cos(position * div_term)return pepe = sinusoidal_pos_encoding(seq_len=10, dim=4)
print(pe)
特点
-
简单,参数量为零(无需学习)。
-
能捕捉到 绝对位置,但无法直接表示相对位置信息。
3. 相对位置编码
原理
相对位置编码(Relative Position Encoding)由 Transformer-XL、T5 等模型引入。它不直接表示某个 token 的绝对位置,而是建模 两个 token 之间的相对距离。例如:
-
词 A 在位置 5
-
词 B 在位置 8
-
相对距离 = 8 - 5 = 3
这样,注意力权重不仅依赖于 $Q, K$ 的相似度,还会额外考虑它们的相对位置信息。
代码示例(简化版)
import torchdef relative_position_matrix(seq_len):# 构建 [i - j] 相对距离矩阵range_vec = torch.arange(seq_len)rel_pos = range_vec[None, :] - range_vec[:, None]return rel_posprint(relative_position_matrix(5))
输出:
tensor([[ 0, -1, -2, -3, -4],[ 1, 0, -1, -2, -3],[ 2, 1, 0, -1, -2],[ 3, 2, 1, 0, -1],[ 4, 3, 2, 1, 0]])
特点
-
能直接捕捉相对关系,更适合长文本。
-
复杂度更高,实现较为复杂。
4. 旋转位置编码(RoPE, Rotary Position Embedding)
原理
RoPE 在 LLaMA 等大模型中被广泛采用。其核心思想是:将每个向量在二维平面上 按位置角度旋转,这样位置信息自然融入 embedding。
数学形式:
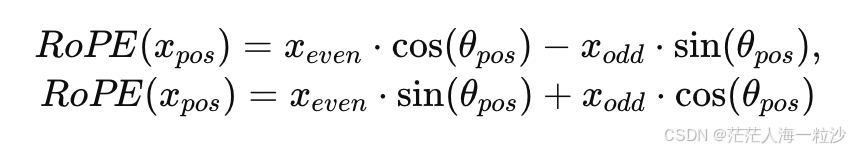
其中 $\theta_{pos}$ 与位置 $pos$ 有关。
代码示例
import torch
import mathdef build_rope_cache(seq_len, dim, base=10000):half_dim = dim // 2freqs = torch.arange(half_dim, dtype=torch.float32)inv_freq = 1.0 / (base ** (freqs / half_dim))t = torch.arange(seq_len, dtype=torch.float32)freqs = torch.outer(t, inv_freq)cos, sin = freqs.cos(), freqs.sin()return cos, sindef apply_rope(x, cos, sin):x1 = x[..., ::2]x2 = x[..., 1::2]cos = cos.unsqueeze(-1)sin = sin.unsqueeze(-1)x1_new = x1 * cos.squeeze(-1) - x2 * sin.squeeze(-1)x2_new = x1 * sin.squeeze(-1) + x2 * cos.squeeze(-1)return torch.stack([x1_new, x2_new], dim=-1).flatten(-2)# 示例
x = torch.randn(4, 4) # 输入向量
cos, sin = build_rope_cache(seq_len=4, dim=4)
x_rope = apply_rope(x, cos, sin)
print(x_rope)
可视化

RoPE 的效果可以用二维向量旋转来理解:同一个向量 [1, 0],随着位置递增被不断旋转,最终形成一个圆形轨迹。这种旋转过程,恰好把位置信息自然编码到向量中。
特点
-
简洁,几何直观。
-
能同时表达绝对和相对位置信息。
-
已成为当前 LLM 的主流选择。
5. 三种方法对比
| 方法 | 是否捕捉相对关系 | 实现复杂度 | 大模型使用情况 |
|---|---|---|---|
| 绝对位置编码 | ❌ | ⭐ | 基础 Transformer |
| 相对位置编码 | ✅ | ⭐⭐⭐ | Transformer-XL, T5 |
| RoPE | ✅ (间接) | ⭐⭐ | GPT-NeoX, LLaMA, ChatGLM |
6. 总结
-
绝对位置编码简单,但无法处理长序列和相对位置信息。
-
相对位置编码更强大,但实现复杂。
-
RoPE 通过旋转实现位置感知,兼具直观性和高效性,已成为当前大模型的事实标准。
随着 LLM 的发展,位置信息的建模方式也在不断演进,而 RoPE 可能会在相当长的一段时间里继续主导大模型的设计。
https://www.interdb.jp/dl/part04/ch17/sec02.html