【硬件-笔试面试题-77】硬件/电子工程师,笔试面试题(知识点:滤波电路中截止频率的计算)
题目汇总版--链接:
【硬件-笔试面试题】硬件/电子工程师,笔试面试题汇总版,持续更新学习,加油!!!-CSDN博客
【硬件-笔试面试题-77】硬件/电子工程师,笔试面试题(知识点:滤波电路中截止频率的计算)
1、题目
滤波电路中截止频率的计算
2、解答
滤波电路的截止频率(又称截止点、半功率点)是指信号功率衰减至输入功率的 1/2(电压 / 电流衰减至 1/√2 ≈ 0.707 倍)时的频率,是衡量滤波电路通带与阻带分界的关键参数。不同类型的滤波电路(RC、RL、LC、有源滤波等),其截止频率的计算方式不同,以下按常见电路类型详细说明:
一、RC 滤波电路(最基础的滤波电路)
RC 电路由电阻(R)和电容(C)组成,分为低通和高通两种,截止频率仅与 R 和 C 的参数相关。
1. RC 低通滤波电路
- 电路结构:输入信号经电阻 R 串联,电容 C 并联接地,输出信号从电容两端取出。
- 工作原理:低频信号可通过电容(容抗大,近似开路),高频信号被电容短路(容抗小)。
- 截止频率公式:\(f_c = \frac{1}{2\pi RC}\) 其中,R 为电阻值(单位:Ω),C 为电容值(单位:F),\(f_c\) 为截止频率(单位:Hz)。
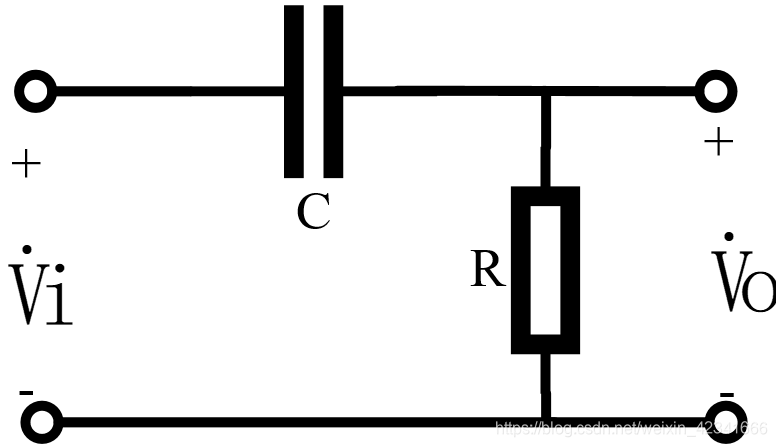
2. RC 高通滤波电路
- 电路结构:输入信号经电容 C 串联,电阻 R 并联接地,输出信号从电阻两端取出。
- 工作原理:高频信号可通过电容(容抗小),低频信号被电容阻断(容抗大)。
- 截止频率公式: 与低通电路相同(因 RC 的阻抗特性对称):\(f_c = \frac{1}{2\pi RC}\)
二、RL 滤波电路(电感与电阻组成)
RL 电路由电阻(R)和电感(L)组成,同样分为低通和高通,截止频率与 R 和 L 相关。
1. RL 低通滤波电路
- 电路结构:输入信号经电感 L 串联,电阻 R 并联接地,输出信号从电阻两端取出。
- 工作原理:低频信号可通过电感(感抗小),高频信号被电感阻断(感抗大)。
- 截止频率公式: 感抗 \(X_L = 2\pi fL\),当 \(X_L = R\) 时(阻抗匹配点),即为截止频率:\(f_c = \frac{R}{2\pi L}\) 其中,R 为电阻值(Ω),L 为电感值(H)。
2. RL 高通滤波电路
- 电路结构:输入信号经电阻 R 串联,电感 L 并联接地,输出信号从电感两端取出。
- 工作原理:高频信号可通过电感(感抗大,近似开路),低频信号被电感短路(感抗小)。
- 截止频率公式: 与低通电路相同(因 RL 的阻抗特性对称):\(f_c = \frac{R}{2\pi L}\)
三、LC 滤波电路(电感与电容组成,无源滤波)
LC 电路利用电感(L)和电容(C)的谐振特性,常见于带通、带阻滤波,或作为高阶滤波的基础单元。
1. LC 串联谐振(带通滤波核心)
- 电路结构:电感 L 与电容 C 串联,输入信号加在串联电路两端,输出信号从负载(或串联节点)取出。
- 谐振特性:当信号频率等于谐振频率时,LC 串联阻抗最小(近似短路),信号衰减最小(通带);偏离谐振频率时,阻抗增大(阻带)。
- 截止频率与谐振频率: 谐振频率(中心频率)\(f_0\) 为:\(f_0 = \frac{1}{2\pi \sqrt{LC}}\) 实际带通滤波的截止频率需结合品质因数(Q)计算,上下截止频率 \(f_{c1}\)(低截止)和 \(f_{c2}\)(高截止)为:\(f_{c1} = f_0 \left( -\frac{1}{2Q} + \sqrt{1 + \left( \frac{1}{2Q} \right)^2} \right)\)\(f_{c2} = f_0 \left( \frac{1}{2Q} + \sqrt{1 + \left( \frac{1}{2Q} \right)^2} \right)\) 其中,品质因数 \(Q = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 CR}\)(R 为电路总电阻),Q 值越大,通带越窄。
2. LC 并联谐振(带阻滤波核心)
- 电路结构:电感 L 与电容 C 并联,输入信号加在并联电路两端,输出信号从负载取出。
- 谐振特性:谐振时并联阻抗最大(近似开路),信号衰减最大(阻带);偏离频率时阻抗减小(通带)。
- 截止频率:与串联谐振类似,上下截止频率围绕谐振频率 \(f_0 = \frac{1}{2\pi \sqrt{LC}}\),计算公式同上(需结合 Q 值)。
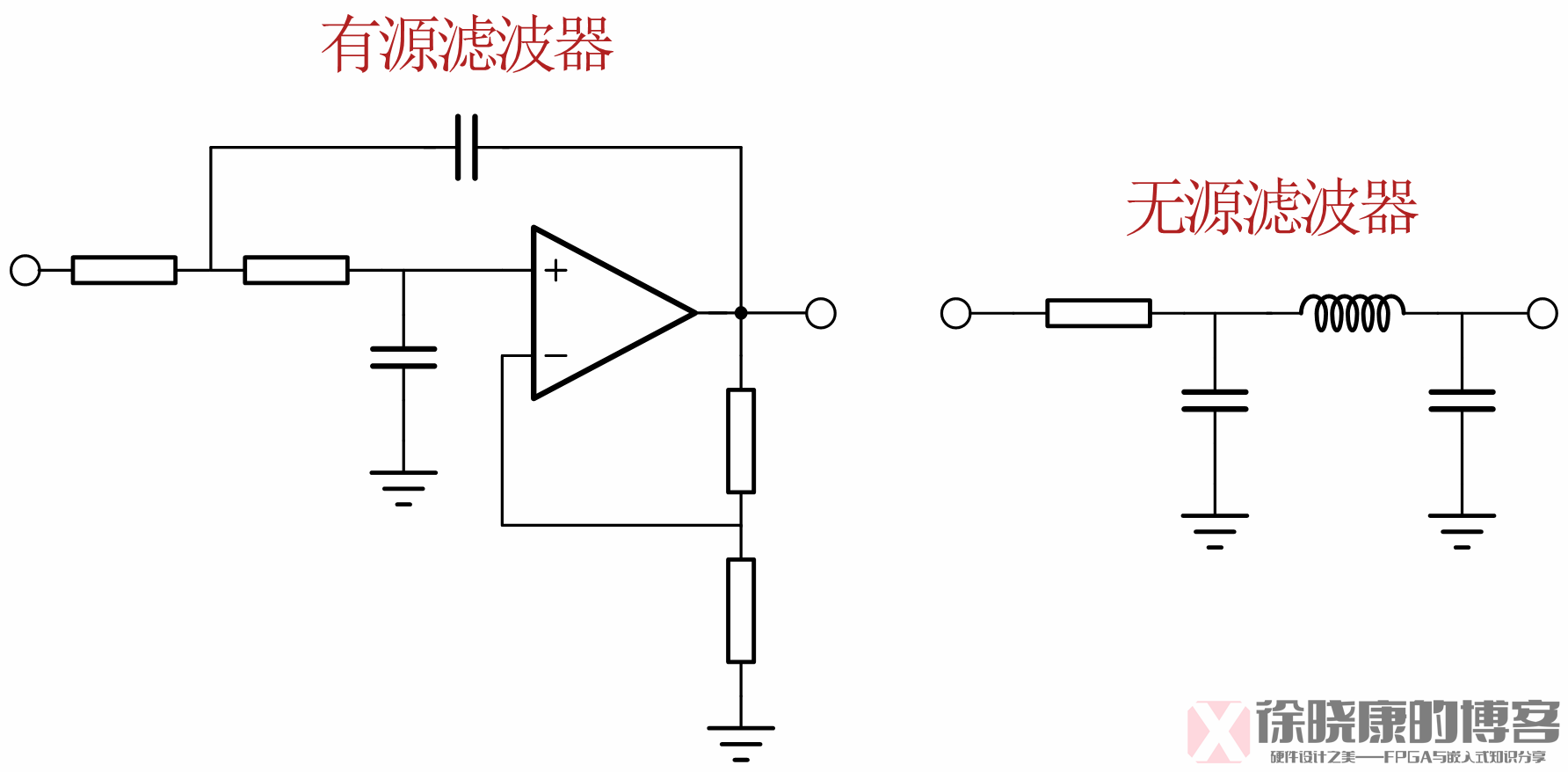
四、有源滤波电路(含运算放大器)
有源滤波电路由 RC 网络与运算放大器组成,可实现低通、高通、带通、带阻等特性,截止频率主要由 RC 网络决定,运算放大器仅起放大或缓冲作用(不影响频率特性)。
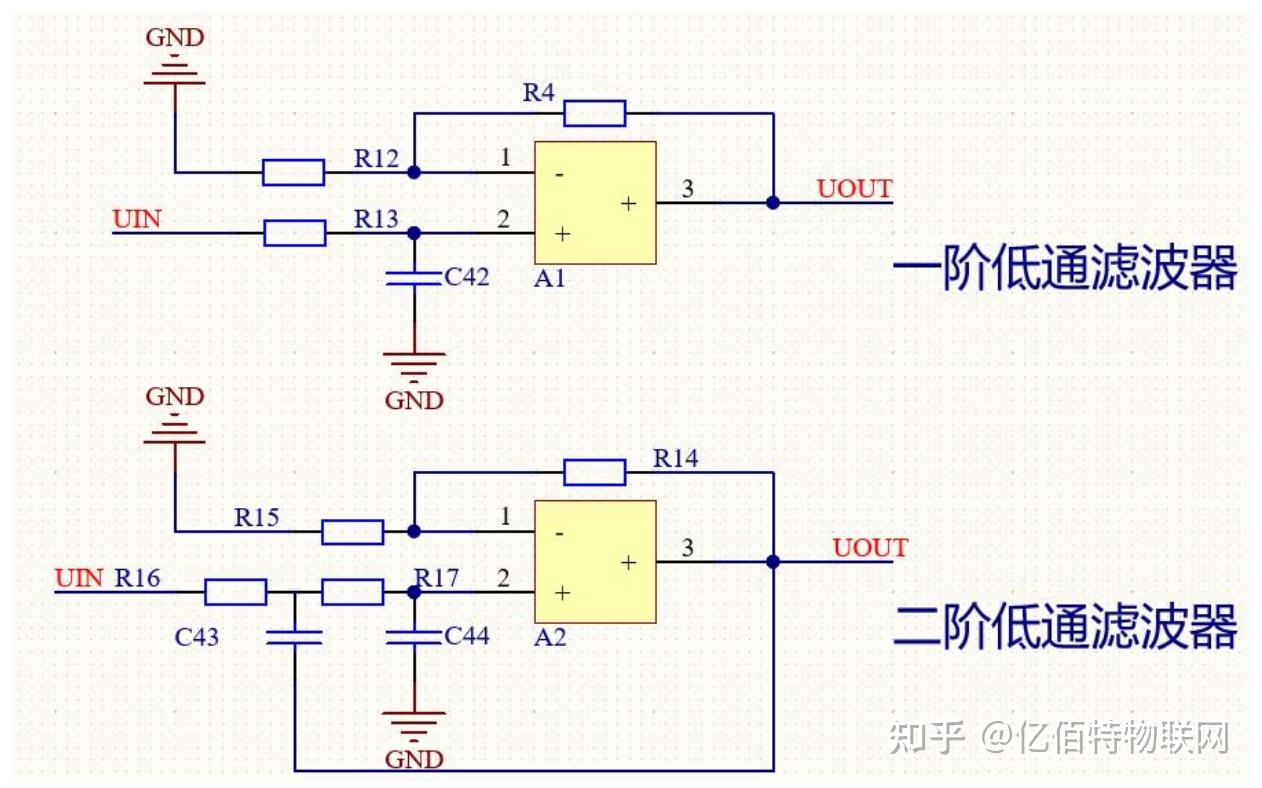
1. 一阶有源低通 / 高通滤波
- 电路结构:在 RC 低通 / 高通电路后级加运算放大器(同相或反相放大)。
- 截止频率:与 RC 滤波电路相同,即 \(f_c = \frac{1}{2\pi RC}\)(低通、高通公式一致)。
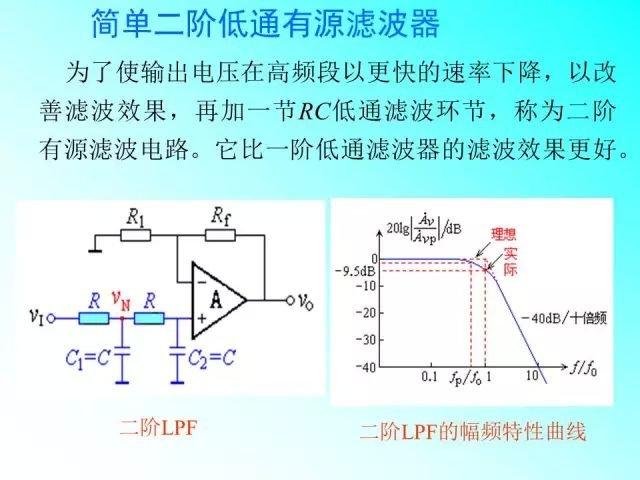
2. 二阶有源滤波(如巴特沃斯滤波)
- 电路结构:由两级 RC 网络与运算放大器组成,可降低通带纹波,提高阻带衰减速度(-40dB / 十倍频,一阶为 - 20dB / 十倍频)。
- 截止频率公式(巴特沃斯型,最平坦通带): 对于二阶低通滤波,截止频率为:\(f_c = \frac{1}{2\pi \sqrt{R_1 R_2 C_1 C_2}}\) 若对称设计(\(R_1 = R_2 = R\),\(C_1 = C_2 = C\)),则简化为:\(f_c = \frac{1}{2\pi RC}\) (注:二阶滤波的元件参数需满足特定比例以实现巴特沃斯特性,如 \(R_2 = 2R_1\) 等,具体需结合电路拓扑。)
五、关键说明
- 截止频率的物理意义:信号在截止频率处衰减 3dB(\(20\log_{10}(1/\sqrt{2}) \approx -3dB\)),并非完全截止,而是通带与阻带的分界点。
- 元件参数误差:实际电路中,电阻、电容、电感的标称值存在误差(如 ±5%、±10%),会导致截止频率偏离理论值,设计时需预留余量。
- 负载影响:无源滤波电路(RC、RL、LC)的截止频率会受负载阻抗影响(负载会改变等效电阻 / 电容),有源滤波因运算放大器输入阻抗高,负载影响可忽略。
- 高阶滤波:三阶及以上滤波电路的截止频率计算需结合传递函数推导,通常基于低阶电路的级联,总截止频率近似等于各阶截止频率的最小值(或通过归一化设计)。
总结
滤波电路的截止频率计算核心是阻抗平衡条件(容抗 = 电阻、感抗 = 电阻、谐振时的阻抗极值),不同电路类型的公式虽有差异,但均围绕 RC、RL 或 LC 的参数展开。实际设计中,需根据滤波类型(低通 / 高通 / 带通)、阶数(一阶 / 二阶)及元件参数选择对应公式,并考虑元件误差和负载影响。
题目汇总--链接:
【硬件-笔试面试题】硬件/电子工程师,笔试面试题汇总版,持续更新学习,加油!!!-CSDN博客

