当前位置：首页 > news >正文

【进阶版两种方法 | 题解】洛谷 P4285 [SHOI2008] 汉诺塔 [数学分析递推]

news 2025/9/9 12:27:45

题面：P4285 [SHOI2008] 汉诺塔 - 洛谷

我想以深入浅出的讲解方式解决这道题，就有了这篇题解。

这里讲的是进阶版的数学做法，需大量推导分析。

如果你只是想学会这道题，看这个足够。

1.前导

先模拟下样例 2：

2
AB BA CA BC CB AC

第一次操作：AB

第二次操作：AC

第三次操作：BA

第四次操作：CB

第五次操作：AB

我们知道，正常 n = 2 汉诺塔的最小转移操作数为 3。

而这里因为 BA 的优先级大于 BC，第三次操作的时候本来应该 BC 直接结束的。

却又整体转移到了 B 轴，5 次才完成。

再看看样例 3：

3
AB BC CA BA CB AC

第一次操作：AB

第二次操作：AC

第三次操作：BC

第四次操作：AB

第五次操作：CA

第六次操作：CB

第七次操作：AB

n = 3 汉诺塔的最小转移操作数正好就是 7，仔细分析发现这个样例满足：

BC 的优先级大于 BA，第三次操作的时候把 n = 2 完美转移到了 C 轴。

CA 的优先级大于 CB，第五次操作时把最小的那个转移到了 A 轴，而不是有最大盘子的 B 轴。

2.进一步猜测 & 暴力代码

我们知道，正常汉诺塔最小转移操作数的递推式长这样：

$f[1]=1$

$f[i]=f[i-1]*2+1\ (i>1)$

猜测：本题同样存在这种线性规律。

我们知道，汉诺塔最终可以转移到 B 轴或者 C 轴。

（以下假设都是正常情况，即最小操作数）

当 n = 2 时，如果 AB 的优先级大于 AC，最后是转移到 C 轴。

那么 n = 3 时，先把 n = 2 转移到 C 轴，最后再全部转回 B 轴。

以此类推，我们就知道了：

if (AB 的优先级大于 AC) {if (n 是偶数) {最后转移到 C 轴; }else {最后转移到 B 轴; }
}
else {if (n 是偶数) {最后转移到 B 轴; }else {最后转移到 C 轴; }
}

所以 AB 和 AC 的优先级之间的大小只决定最后转移到哪个轴，和方案数没任何关系。

在开始之前，hansang 要送给你们一个东西：

#include<bits/stdc++.h>
using namespace std;char s[7][5];
int sta[4][35], len[4], n;bool pd() {int flagb = 1;for (int i = 1; i <= n; i++) {if (sta[2][i] != n - i + 1) {flagb = 0;break;}}int flagc = 1;for (int i = 1; i <= n; i++) {if (sta[3][i] != n - i + 1) {flagc = 0;break;}}return flagb | flagc;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;for (int i = 1 ; i <= 6; i ++) {cin >> s[i];}for (int i = 1; i <= n; i++) {sta[1][i] = n - i + 1;}len[1] = n;len[2] = len[3] = 0;int last = 0, sum = 0;while (pd() == 0) {for (int i = 1; i <= 6; i++) {int st = s[i][0] - 'A' + 1;int ed = s[i][1] - 'A' + 1;if (last == sta[st][len[st]] || len[st] == 0) {continue;}if (len[ed] == 0 || (sta[st][len[st]] < sta[ed][len[ed]])) {last = sta[st][len[st]];len[ed] ++;sta[ed][len[ed]] = sta[st][len[st]];len[st] --;sum ++;cout << sum << " " << s[i] << "\n";break;}else {continue;}}}return 0;
}

这个代码如果输入样例 1，就会输出：

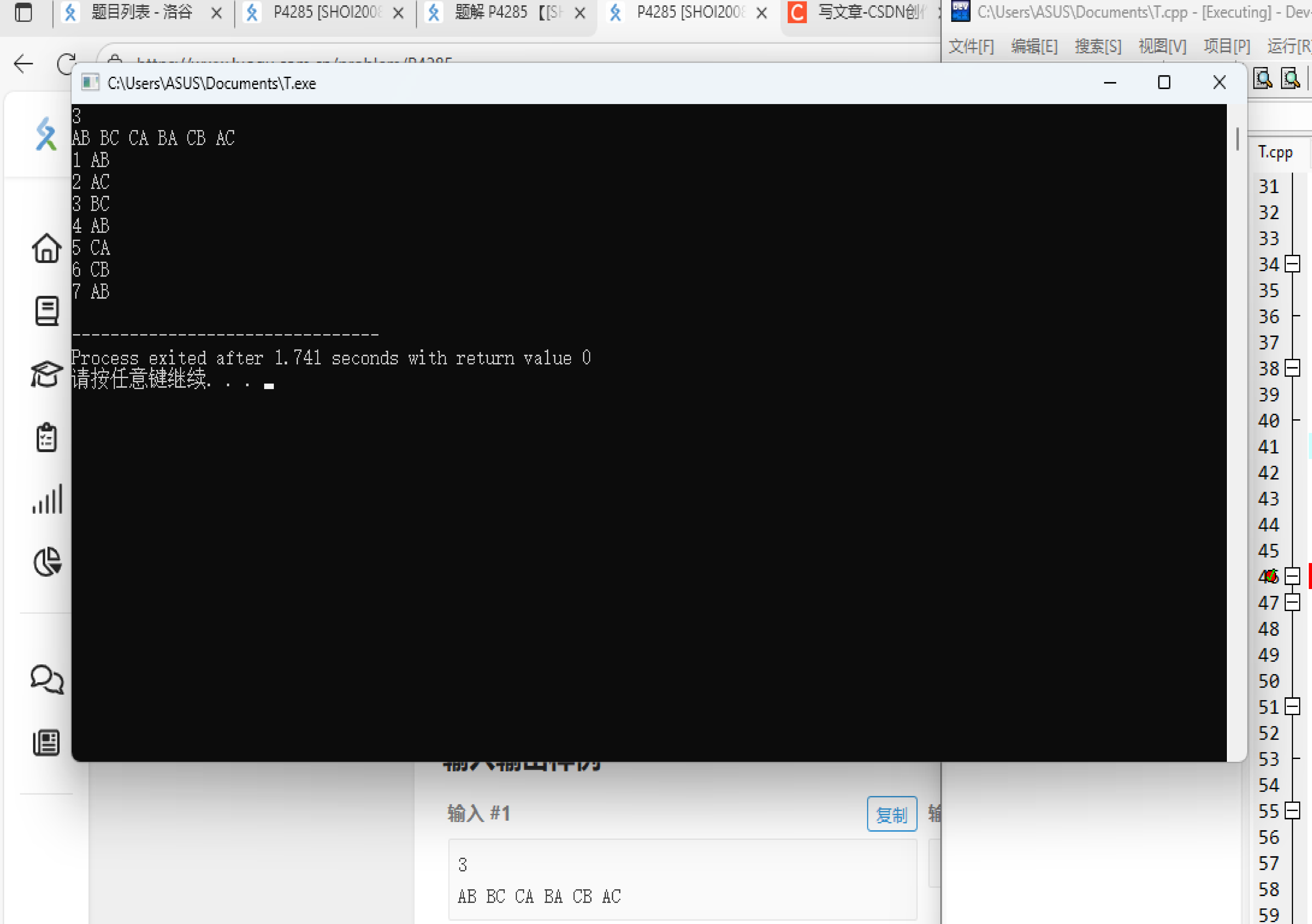
下面会用到啦^^

3.分析

考虑别的优先级比较对，我们先想 $n\leq 3$ 的情况：

（以下假设都建立在 AB 的优先级大于 AC 的情况下）

（以下优先级比较对，都是试样例试出来的那几对）

（1）当 n = 2 时：

如果 BC 的优先级大于 BA，那么 $f[2] = 3$ （正常情况，转移到 C 轴）。

如果 BA 的优先级大于 BC，那么 $f[2] = 5$ （转移到 B 轴）。

（2）当 n = 3 时：

如果 BC 的优先级大于 BA，那么：

有 $f[2] = 3$ （正常情况，转移到 C 轴）。

如果 CA 的优先级大于 CB，那么 $f[3] = 7$ （正常情况）。

如果 CB 的优先级大于 CA，那么 $f[3] = 9$ 。

请看流程图：

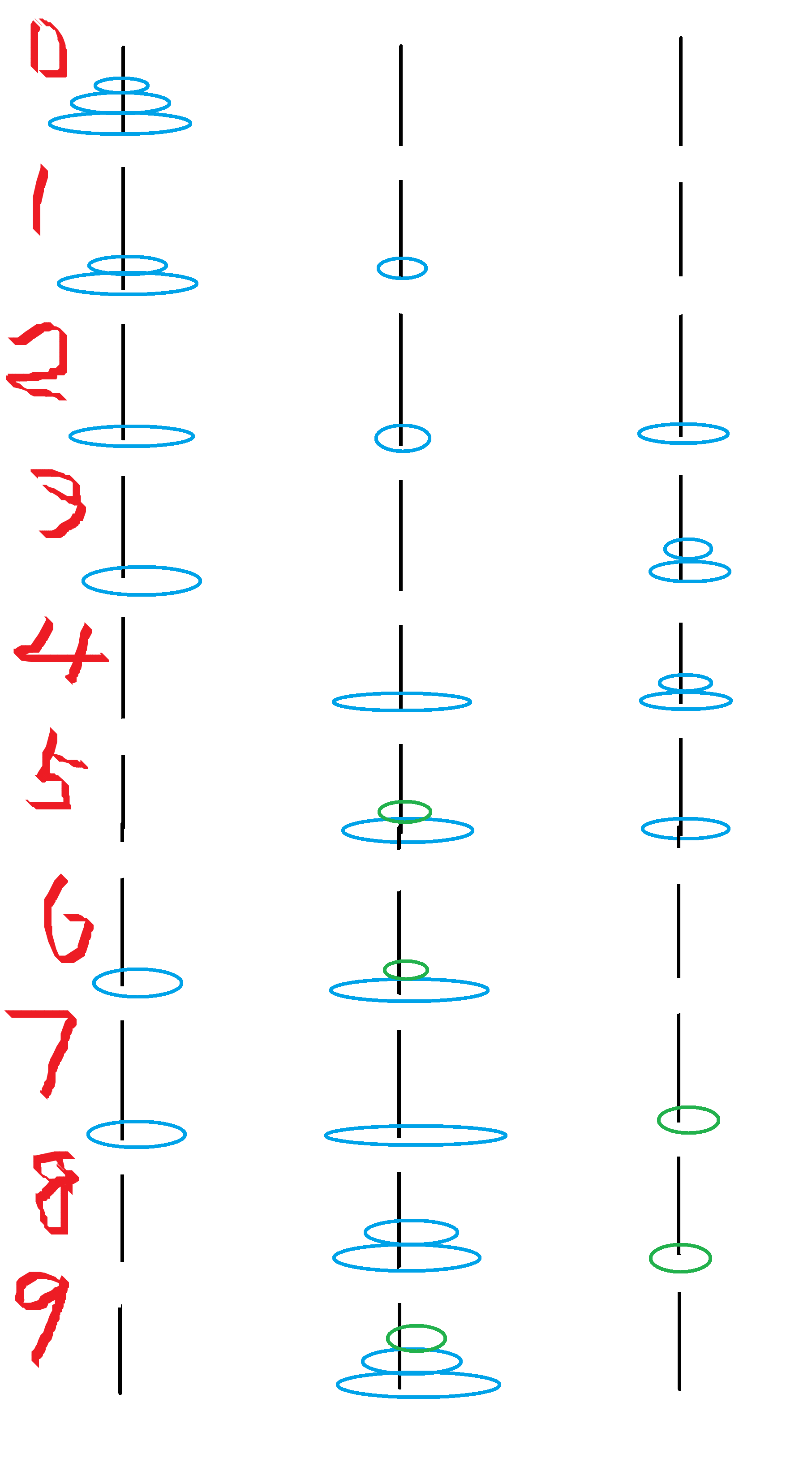
在第五步操作的时候，绿色的最小盘子应该放到 A 轴，却放在了 B 轴。

其实从第四步结束开始，就可以看作 C 是开始轴，要把 n = 2 转移到 B 轴。

那我们现在已有的条件：

AB > AC，BC > BA，CB > CA

把这些条件中的 A 和 C 互换，因为我们从 C 开始，就得到：

CB > CA，BA > BC，AB > AC

我们发现在这个情况下， $f ' [2]$ 为 $5$ ，最后是转移到 B 轴。

（详见（1）当 n = 2 时的第二种情况）

那么方案数就等于：

$f[3] = f[2]$ （一开始把 n = 2 转移到 C 轴） $+ 1$ （第四步转移大盘子） $+ f ' [2] = 9$

如果 BA 的优先级大于 BC，那么：

有 $f[2] = 5$ （转移到 B 轴）。

如果 CA 的优先级大于 CB，因为这个时候把 n = 2 都转移到 B 轴了，

现在把最大的盘子转移到 C 轴，需要操作一次。

再从 B 轴的 n = 2 转移到 C 轴。

我们再整理下现在已经有的条件：

AB > AC，BA > BC，CA > CB

把这些条件中的 A 和 B 互换，因为我们从 B 开始，就得到：

BA > BC，AB > AC，CB > CA

我们发现在这个情况下，f[2] 仍然为 5，但是最后是转移到 A 轴。

（详见（1）当 n = 2 时的第二种情况）

用刚才给的程序，输入：

3
AB BA BC CA CB AC

输出：

1 AB
2 AC
3 BA
4 CB
5 AB
6 AC
7 BA
8 BC
9 AB
10 CA
11 BA
12 CB
13 AB
14 AC
15 BA
16 CB
17 AB

我们发现，其中 1 到 5 行都是 n = 2 时的转移，最后转到 B 轴。

第 6 行是大盘子转移，7 到 11 行是 n = 2 的转移，最后到 A 轴。

但第 12 行并没有马上把 A 轴的 n = 2 转移回去，而是动了 C 轴的最大盘子到 B 轴。

（因为不能两次都转一个盘子，就是最小的那个）

所以最后答案：

$f[3] = f[2] + 1 + f[2] + 1 + f[2] = 17$

如果 CB 的优先级大于 CA，和上面同理。

从 AB > AC，BA > BC，CB > CA，变成了：

BA > BC，AB > AC，CA > CB，最后一个条件无伤大雅， $f[2]$ 还是 $5$ 。

所以还是 $f[3] = f[2] + 1 + f[2] + 1 + f[2] = 17$

如果反过来 AC 的优先级大于 AB，那么只要把上述分类的 B 和 C 交换下就好，

结论还可以沿用。

讲到这里，你会发现：

本题确实存在这种线性规律。

也就是 $f[n]$ 都可以从 $k * f[n - 1] + b$ 递推过来。

3.关系式分析 & 两份正确代码

其实到这里，就可以对应具体情况赋值 $f[2]$ 和 $f[3]$ 然后递推了。

就像这个代码：

#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 35;
int mp[300][300];
LL f[N];int main() {ios::sync_with_stdio(false);cin.tie(0);int n;cin >> n;for (int i = 1; i <= 6; i ++) {char s[5];cin >> s;mp[s[0]][s[1]] = 6 - i;   //优先级得倒一下 }f[1] = 1;if (mp['A']['B'] > mp['A']['C']) {if (mp['B']['C'] > mp['B']['A']) {f[2] = 3;if (mp['C']['A'] > mp['C']['B']) {f[3] = 7;}else {f[3] = 9;}}else {f[2] = 5;f[3] = 17;}}else {if (mp['C']['B'] > mp['C']['A']) {f[2] = 3;if (mp['B']['A'] > mp['B']['C']) {f[3] = 7;}else {f[3] = 9;}}else {f[2] = 5;f[3] = 17;}}LL k = f[3] / f[2];LL b = f[3] - k * f[2]; for (int i = 4; i <= n; i++) {f[i] = f[i - 1] * k + b; }cout << f[n] << "\n";return 0;
}

是能提交正确的，复杂度为 $O(N)$ 。

但是，如果我们想要更明确、直接的关系式呢？

我们发现，本质不同的 f 可以分成三种：

当 AB > AC，BC > BA，CA > CB， $f1[2] = 3,f1[3] = 7$

当 AB > AC，BC > BA，CB > CA， $f2[2] = 3,f2[3] = 9$

当 AB > AC，BC > BA， $f3[2] = 5,f3[3] = 17$

同时 $f1[1] = f2[1] = f3[1] = 1$

第一种是正常的， $f1[3] = f1[2] * 2 + 1 = 7$

可以归纳递推式： $f1[n] = f1[n - 1] * 2 + 1$

把 $f1[3]$ 展开来看看： $f1[3] = (f1[1] * 2 + 1) * 2 + 1 = f1[1] * 4 + 2 + 1$

同样的，展开 $f1[4] = ((f1[1] * 2 + 1) * 2 + 1) * 2 + 1 = f1[1] * 8 + 4 + 2 + 1$

发现规律： $f1[n]=2^{n-1}+2^{n-1}-1=2^n-1$

第二种先跳过，我们看第三种：

$f3[2] = 5, \ f3[3] = f3[2] + 1 + f3[2] + 1 + f3[2] = 17$

也就是 $f3[3] = f3[2] * 3 + 2$

归纳递推式： $f3[n] = f3[n - 1] * 3 + 2$

把 $f3[3]$ 展开来看看： $f3[3] = (f3[1] * 3 + 2) * 3 + 2 = f3[1] * 9 + 6 + 2$

同样的，展开 $f3[4] = ((f3[1] * 3 + 2) * 3 + 2) * 3 + 2$

$= f3[1] * 27 + 18 + 6 + 2$

$= f3[1] * 27 + 2 * (1 + 3 + 9)$

这个 $(1 + 3 + 9)$ 是个等比数列，代入求和公式求解。

发现规律： $f3[n]=3^{n-1}+2*(\frac{3^{n-1}-1}{2})=2*3^{n-1}-1$

回来第二种， $f2[3] = f2[2] + 1 + f ' [2] = 9$ 。

这里的 $f ' [2]$ 为 $5$ ，是 $f3[2]$ 。

所以： $f2[3] = f2[2] + 1 + f3[2]$

归纳递推式： $f2[n] = f2[n - 1] + 1 + f3[n - 1]$

把 f2[3] 展开来看看： $f2[3]=f2[2]+1+f3[2]$

$=f2[1]+1+f3[1]+2*3-1$

$=2+2*3$

$=3*3$

同样的，展开 $f2[4] = f2[3]+1+f3[3]$

$= 3*3+1+ 2*3^2-1$

$=3^3$

好像还是不太够，正经归纳下：

设 $f2[n-1]=3^{n-2}$ ，

那么就有： $f2[n]=3^{n-2}+1+2*3^{n-2}-1=3^{n-1}$

发现规律： $f2[n]=3^{n-1}$

因为，所以也就有：

$f1[n]=2^n-1$

$f2[n]=3^{n-1}$

$f3[n]=2*3^{n-1}-1$

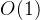好啦，直接 $O(1)$ 解决：

#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 35;
int mp[300][300];LL q_pow(LL a, LL b) {LL c = 1;while (b) {if (b & 1) {c = c * a;}a = a * a;b >>= 1;}return c;
} int main() {ios::sync_with_stdio(false);cin.tie(0);int n;cin >> n;for (int i = 1; i <= 6; i ++) {char s[5];cin >> s;mp[s[0]][s[1]] = 6 - i;   //优先级得倒一下 }int p;if (mp['A']['B'] > mp['A']['C']) {if (mp['B']['C'] > mp['B']['A']) {if (mp['C']['A'] > mp['C']['B']) {p = 1;}else {p = 2;}}else {p = 3;}}else {if (mp['C']['B'] > mp['C']['A']) {if (mp['B']['A'] > mp['B']['C']) {p = 1;}else {p = 2;}}else {p = 3;}}LL ans;if (p == 1) {ans = q_pow(2, n) - 1;}else if (p == 2) {ans = q_pow(3, n - 1);}else {ans = 2 * q_pow(3, n - 1) - 1;}cout << ans << "\n";return 0;
}