MATLAB的数值计算（三）曲线拟合与插值

一、曲线拟合

在许多实际应用中，常常只能测得一些分散的数据点。为了能从这些分散的数据点中找出它们内在的变化规律，人们就依据这些分散的数据点，运用最小二乘法，生成一个函数来逼近这些已知的数据点，称为曲线拟合。曲线拟合对应的命令是polyfit，调用格式为：

polyfit（x，y，n）

其中，x，y为样本数据；n为拟合多项式的阶数；返回值是一个多项式系数的行向量。

在使用polyfit函数的时候，x，y为已知样本数据，n需要设计者自己确定。如果选择n=1，即把样本数据作为直线对待，称为线性回归。

例：已知热敏电阻实验数据如下表所示，利用polyfit函数求其最小二乘法拟合曲线，并计算其误差程度。

温度t/()	20.5	32.7	51.0	73.0	95.7
电阻	765	826	873	942	1032

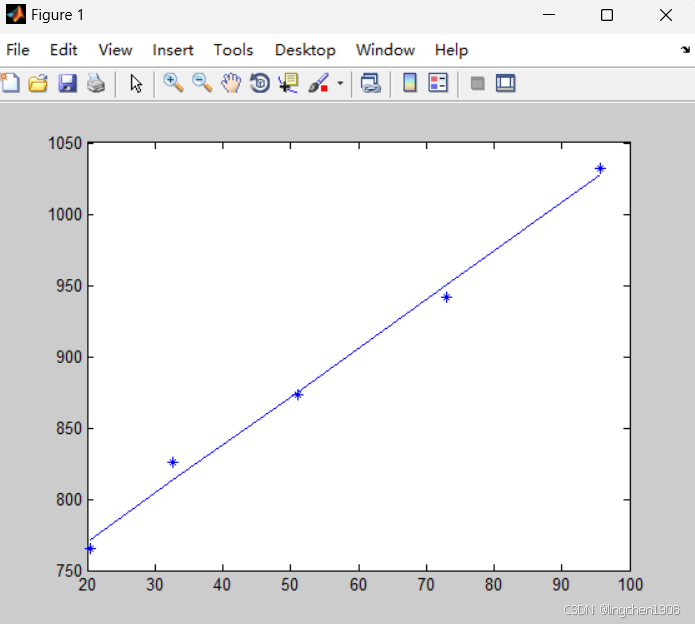
为了对比拟合的多项式与原来样本数据的拟合程度，通过绘图进行观察。

误差计算有很多种方法，在这里使用均方差（Mean Square Error，MSE）的方法来计算，具体计算公式为

其中，n为样本数量，为拟合值，y为样本值。

误差的计算代码如下：

方法1：直接使用一次曲线进行计算。

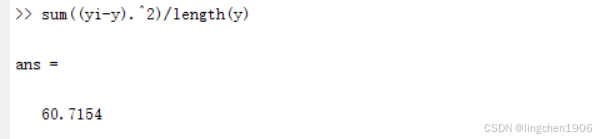
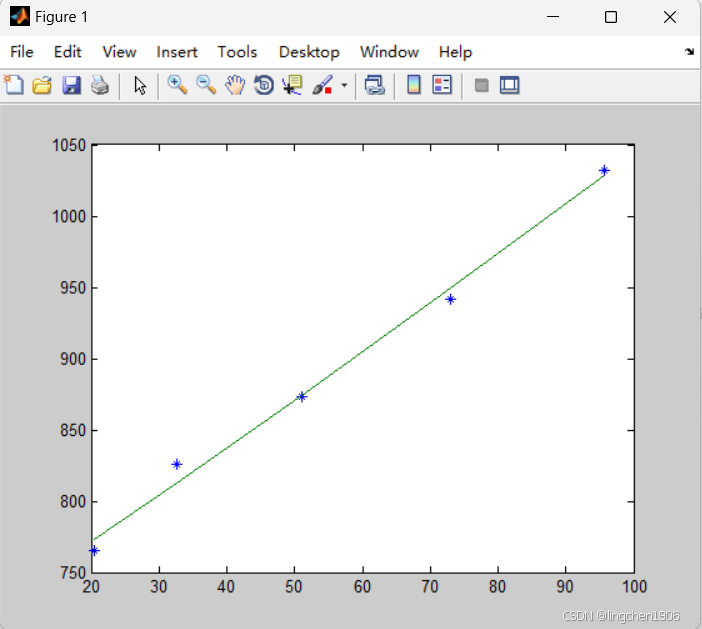
方法2：使用二次曲线进行计算。

二、插值

插值是在已知数据点之间计算估计值。通过这些插值，可以将无规律、没有联系的数据点，连接得到一个近似的曲线。对应一、二维插值的调用命令如下：

yi = interp1(x,y,xi,'method'）

zi =interp2 (x,y,z,xi,yi,'method')

其中，x，y为样本数据；xi是计算的x的位置；method为所用的插值方法，无论是一维插值还是二维插值，method有以下4种选择方法。

方法	Nearest	Linear	Spline	Cubic
说明	邻近点插值	线性插值（默认方法）	3次样条插值	立方插值

例：通过下表中的已知数据求自变量x在[0:0.25:10]等位置的插值，并且画出相应的曲线。

ｘ	0	1	2	3	4	5	6	7	8	9	10
ｙ	0	0.8415	0.9039	0.1411	－0.7568	－0.9589	－0.2794	0.6570	0.9894	0.4121	－0.5440