金融量化指标--3Beta 贝塔
beta计算公式

添加图片注释,不超过 140 字(可选)
一、贝塔(Beta)的核心定义:它是什么?
贝塔(β) 是一个衡量单个证券(或投资组合)相对于整个市场系统性风险的指标。它量化了该资产收益对市场收益变动的敏感程度。
市场基准:通常,这个“市场”用一个广基市场指数来代表,例如:
美国股市:S&P 500指数
中国A股:沪深300指数
全球股市:MSCI全球指数
系统性风险:也称为不可分散风险或市场风险。这是指影响所有资产的宏观因素带来的风险,如利率变化、通货膨胀、经济衰退、战争等。这种风险无法通过分散投资来消除。贝塔衡量的正是这种风险。
二、贝塔的计算方法与数据来源
贝塔的计算基于资本资产定价模型(CAPM) 的统计原理,主要通过线性回归完成。
1. 计算公式:
最常用的计算公式是:
β = Cov(Ri, Rm) / Var(Rm)
Cov(Ri, Rm): 个股(或组合)收益率 Ri 与市场收益率 Rm 的协方差。它衡量两者之间的协同变动关系。
Var(Rm): 市场收益率 Rm 的方差。它衡量市场整体的波动程度。
简单来说,贝塔就是个股与市场的协方差 除以 市场的方差。
2. 回归模型:
在统计学上,我们通过将个股收益率对市场收益率进行线性回归来得到贝塔: Ri = α + β * Rm + ε
Ri: 个股收益率
Rm: 市场收益率
α (Alpha): 回归的截距项,代表超额收益(与市场波动无关的部分)。
β (Beta): 回归的斜率,就是我们要求的贝塔系数。
ε: 残差项,代表公司特有的非系统性风险。
3. 数据来源与实操:
收益率:通常使用每日或每周的收盘价计算对数收益率或简单收益率。
时间窗口:通常使用过去2-5年的历史数据(例如,过去3年的每周收益率)。时间窗口的选择会影响贝塔值的稳定性。太短则噪音多,太长则可能无法反映公司最新的风险特征。
工具:可以使用Excel、Python(Pandas, NumPy, Statsmodels库)、R语言或任何金融数据终端(如Bloomberg、Wind、Yahoo Finance)轻松计算。
三、如何解读贝塔值?
贝塔值的解读是其核心价值所在。通常我们以 β = 1 作为市场平均风险的基准线。
Beta值 (β) | 解读 | 含义 | 例子 |
|---|---|---|---|
β = 1 | 平均风险 | 该股票的价格预期与市场同涨同跌,波动幅度与市场一致。 | 一只大型蓝筹股,其业务与整体经济紧密相连。 |
β > 1 | 高风险 | 该股票的波动性大于市场波动。市场上涨时,它涨得更多;市场下跌时,它也跌得更狠。这类资产称为“进攻型”资产。 | 科技股、小盘股、券商股、周期性行业(如房地产、半导体)。 |
β < 1 | 低风险 | 该股票的波动性小于市场波动。市场大涨时,它涨得少;市场大跌时,它也跌得少。这类资产称为“防御型”资产。 | 公用事业、必需消费品、黄金ETF、大型稳健的食品公司。 |
β = 0 | 无市场风险 | 该股票的收益与市场收益完全没有相关性。(理论上存在,现实中极少) | 理论上,无风险资产(如短期国债)的贝塔为0。 |
β < 0 | 负相关 | 该股票的价格变动方向与市场相反。市场下跌时,它反而上涨。 | 黄金(有时)、做空市场的ETF(如SDS)、某些避险货币。 |
四、贝塔的实际应用
资产定价与预期回报(CAPM模型): 这是贝塔最经典的应用。CAPM模型使用贝塔来计算一项资产的理论预期收益率。 E(Ri) = Rf + βi * [E(Rm) - Rf]
E(Ri): 资产i的预期收益率
Rf: 无风险利率(如国债收益率)
[E(Rm) - Rf]: 市场风险溢价
贝塔是关键:投资者要求更高的预期回报来补偿承担更高的系统性风险(更高的贝塔)。
投资组合管理:
风险控制:基金经理可以根据市场预期调整投资组合的整体贝塔。
看涨市场:增加高贝塔股票的仓位,以期获得超越市场的收益。
看跌市场:降低组合整体贝塔,增持低贝塔或负贝塔资产,以防御市场下跌。
对冲:可以通过做空高贝塔资产来对冲市场下跌对投资组合的影响。
业绩评估: 在评估基金经理的业绩时,不能只看绝对收益。如果一个基金获得了15%的回报,但它的贝塔是1.5,那么它承担了更高的风险,其经过风险调整后的收益(如夏普比率)可能并不出色。
资本成本计算: 公司在进行投资决策时,会使用加权平均资本成本(WACC)作为折现率。其中,股权成本(Cost of Equity)通常通过CAPM模型计算,贝塔是其中的核心输入变量。
五、贝塔的局限性与批判
贝塔是一个有用的工具,但绝不能盲目使用。它有以下显著局限性:
依赖历史数据:贝塔是用过去的数据计算的,但投资是面向未来的。公司的业务、资本结构或市场环境发生变化时,历史的贝塔可能无法准确预测未来的风险。这被称为“未来贝塔的不稳定性”。
对市场代理指数的敏感性:贝塔值取决于你选择什么作为“市场”。用S&P 500还是Russell 2000?用沪深300还是中证500?选择不同的指数会得到不同的贝塔值。
忽略非系统性风险:贝塔只捕捉了系统性风险,完全忽略了公司特有的风险(如管理层失误、产品失败、工厂事故等)。而这些风险可以通过分散投资来降低。
假设线性关系:贝塔假设股票与市场的关系是线性的。但实际上,在市场极端暴跌(如金融危机)时,所有资产的相关性都会趋近于1,这种非线性关系是贝塔无法捕捉的。
不考虑下行风险:贝塔衡量的是双向波动。一个上下波动都很剧烈的股票和一个只在大盘跌时剧烈下跌、大盘涨时却涨得不多的股票,可能拥有相同的贝塔值,但显然后者的风险体验更差。
六、贝塔与其他风险指标的关系
Alpha (α): 超额收益。衡量投资策略相比市场(经贝塔调整后)的表现。α > 0 表示跑赢市场,α < 0 表示跑输市场。“赚Alpha”是主动投资者追求的目标。
标准差: 衡量总波动性(总风险),既包括系统性风险(贝塔),也包括非系统性风险。贝塔只衡量其中的系统性部分。
R-squared (R²): 在回归中,R²表示股票收益率的变化中有多大比例可以由市场收益率的变化来解释。高贝塔 + 高R² 意味着波动主要来自市场;高贝塔 + 低R² 意味着波动可能来自公司自身特质,贝塔的参考价值较低。
总结
贝塔(Beta)是一个强大而基础的金融量化工具,它成功地将“风险”用一个简单的数字来量化。它对于理解资产相对于市场的波动特性、进行资产定价和构建投资组合至关重要。
然而,它绝非完美的风险度量标准。聪明的投资者会将贝塔作为一个重要的参考指标,但同时必须意识到其基于历史数据的局限性,并结合其他指标(如Alpha、标准差、夏普比率)以及对公司基本面的定性分析,才能做出更全面、更明智的投资决策。
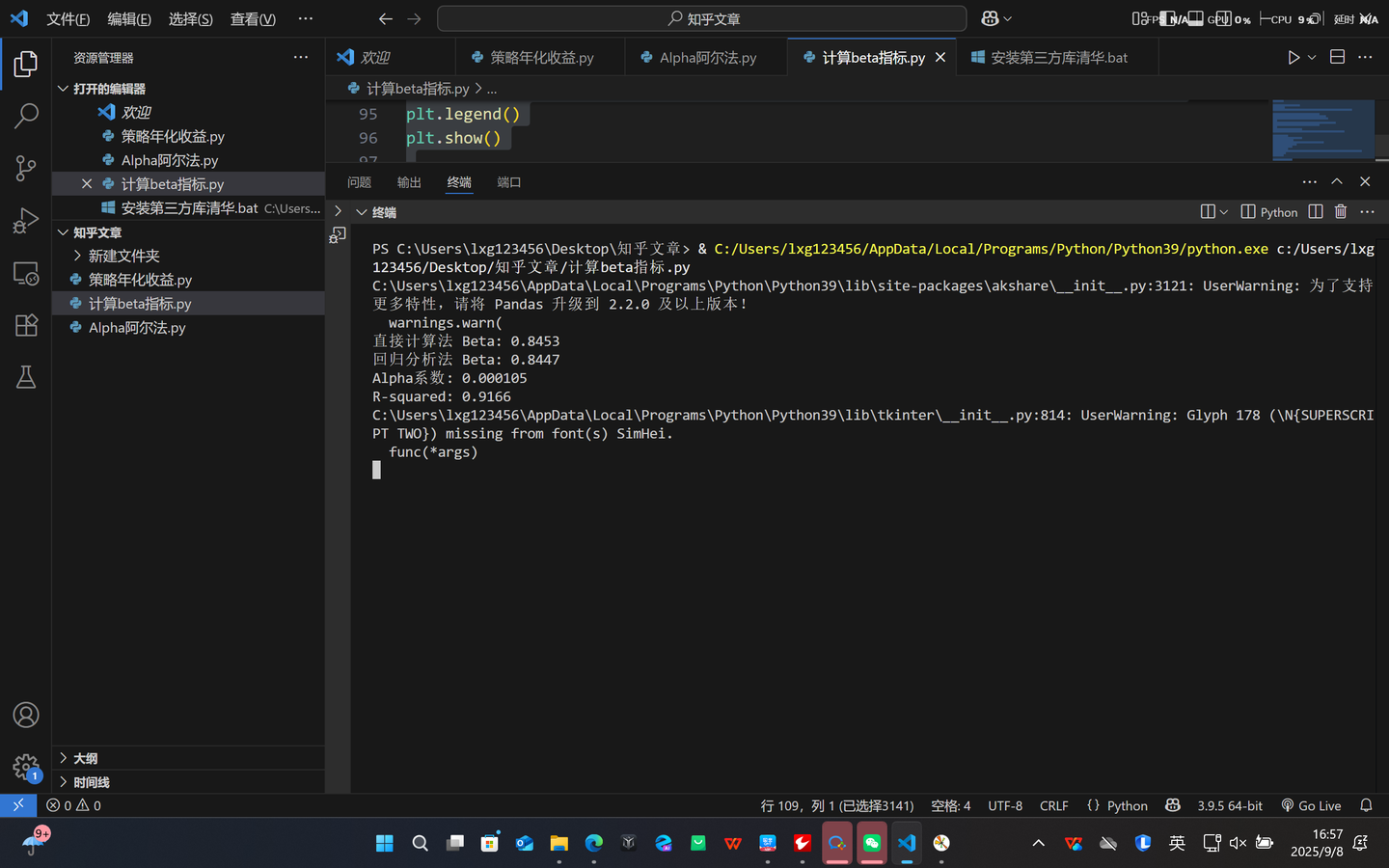
python计算源代码计算的结果
添加图片注释,不超过 140 字(可选)
添加图片注释,不超过 140 字(可选)
计算源代码
# 导入必要的库
import akshare as ak
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 设置参数
ticker = 'sh000001' # 股票代码
market_index = '000300' # 市场指数代码(S&P 500)
start_date = '20200101'
end_date = '20250905'
stock_df=ak.stock_zh_a_daily(symbol=ticker,start_date=start_date,end_date=end_date)
index_df=ak.index_zh_a_hist(symbol=market_index,start_date=start_date,end_date=end_date)# 确保日期对齐
aligned_data = pd.DataFrame({'stock_returns': stock_df['close'].pct_change(),'market_returns': index_df['收盘'].pct_change()
}).dropna()stock_returns = aligned_data['stock_returns']
market_returns = aligned_data['market_returns']# 方法1: 使用协方差和方差公式直接计算Beta
covariance = np.cov(stock_returns, market_returns)[0][1]
market_variance = np.var(market_returns)
beta_direct = covariance / market_varianceprint(f"直接计算法 Beta: {beta_direct:.4f}")# 方法2: 使用线性回归计算Beta
# 准备数据
X = market_returns.values
y = stock_returns.values# 添加常数项(截距)
X_with_const = np.column_stack([np.ones(len(X)), X])# 使用最小二乘法进行回归
beta_regression = np.linalg.inv(X_with_const.T @ X_with_const) @ X_with_const.T @ y
alpha = beta_regression[0]
beta_regression = beta_regression[1]print(f"回归分析法 Beta: {beta_regression:.4f}")
print(f"Alpha系数: {alpha:.6f}")# 计算R-squared
y_pred = alpha + beta_regression * X
ss_res = np.sum((y - y_pred) ** 2)
ss_tot = np.sum((y - np.mean(y)) ** 2)
r_squared = 1 - (ss_res / ss_tot)print(f"R-squared: {r_squared:.4f}")# 绘制散点图和回归线
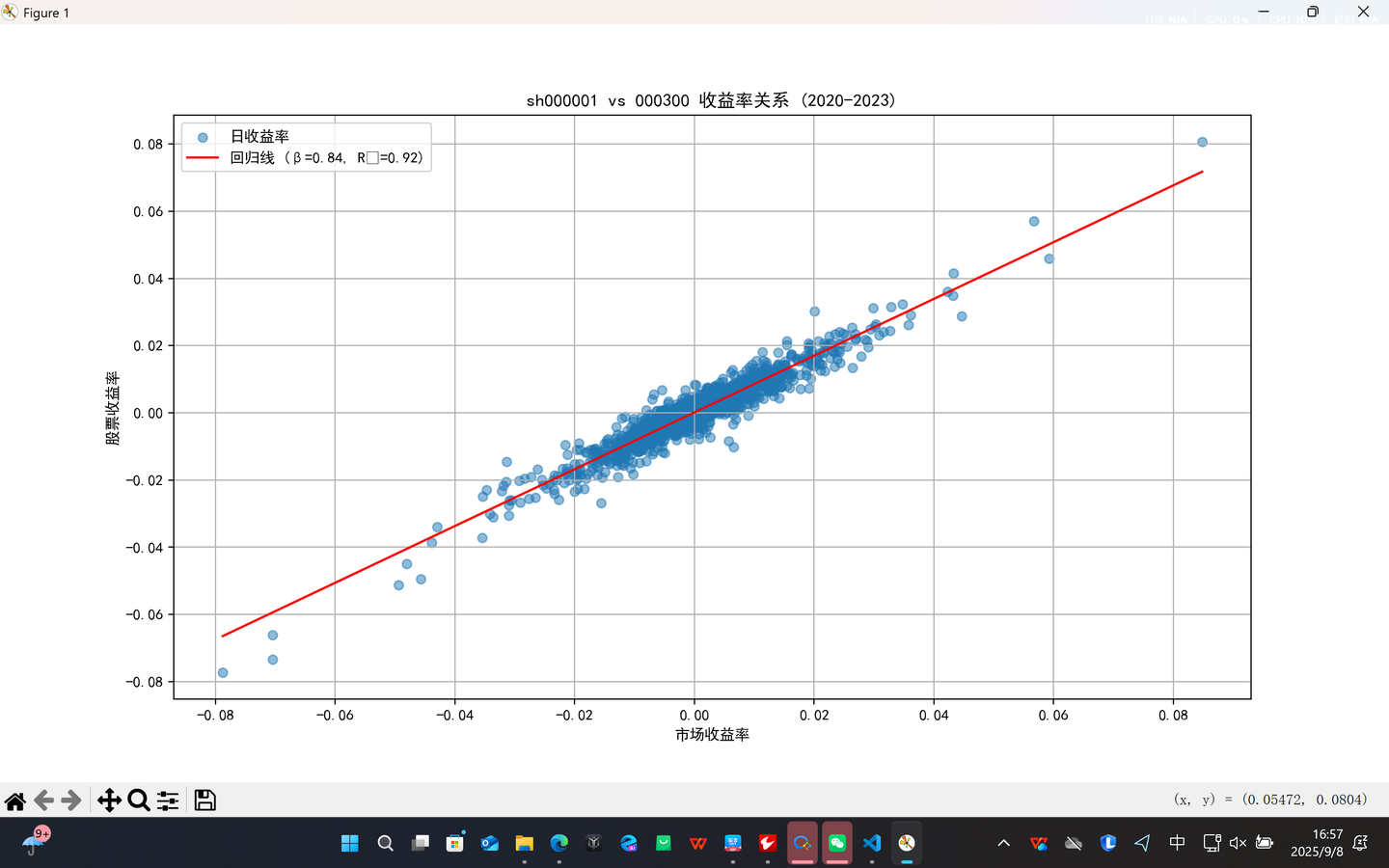
plt.figure(figsize=(10, 6))
plt.scatter(market_returns, stock_returns, alpha=0.5, label='日收益率')# 绘制回归线
x_range = np.linspace(min(market_returns), max(market_returns), 100)
plt.plot(x_range, alpha + beta_regression * x_range, 'r-', label=f'回归线 (β={beta_regression:.2f}, R²={r_squared:.2f})')plt.xlabel('市场收益率')
plt.ylabel('股票收益率')
plt.title(f'{ticker} vs {market_index} 收益率关系 (2020-2023)')
plt.legend()
plt.grid(True)
plt.show()# 计算滚动Beta (90天窗口)
window = 90
rolling_beta = pd.Series(index=stock_returns.index[window:], dtype=float)for i in range(window, len(stock_returns)):stock_window = stock_returns.iloc[i-window:i]market_window = market_returns.iloc[i-window:i]covariance = np.cov(stock_window, market_window)[0][1]market_variance = np.var(market_window)if market_variance > 0:rolling_beta.iloc[i-window] = covariance / market_variance# 绘制滚动Beta
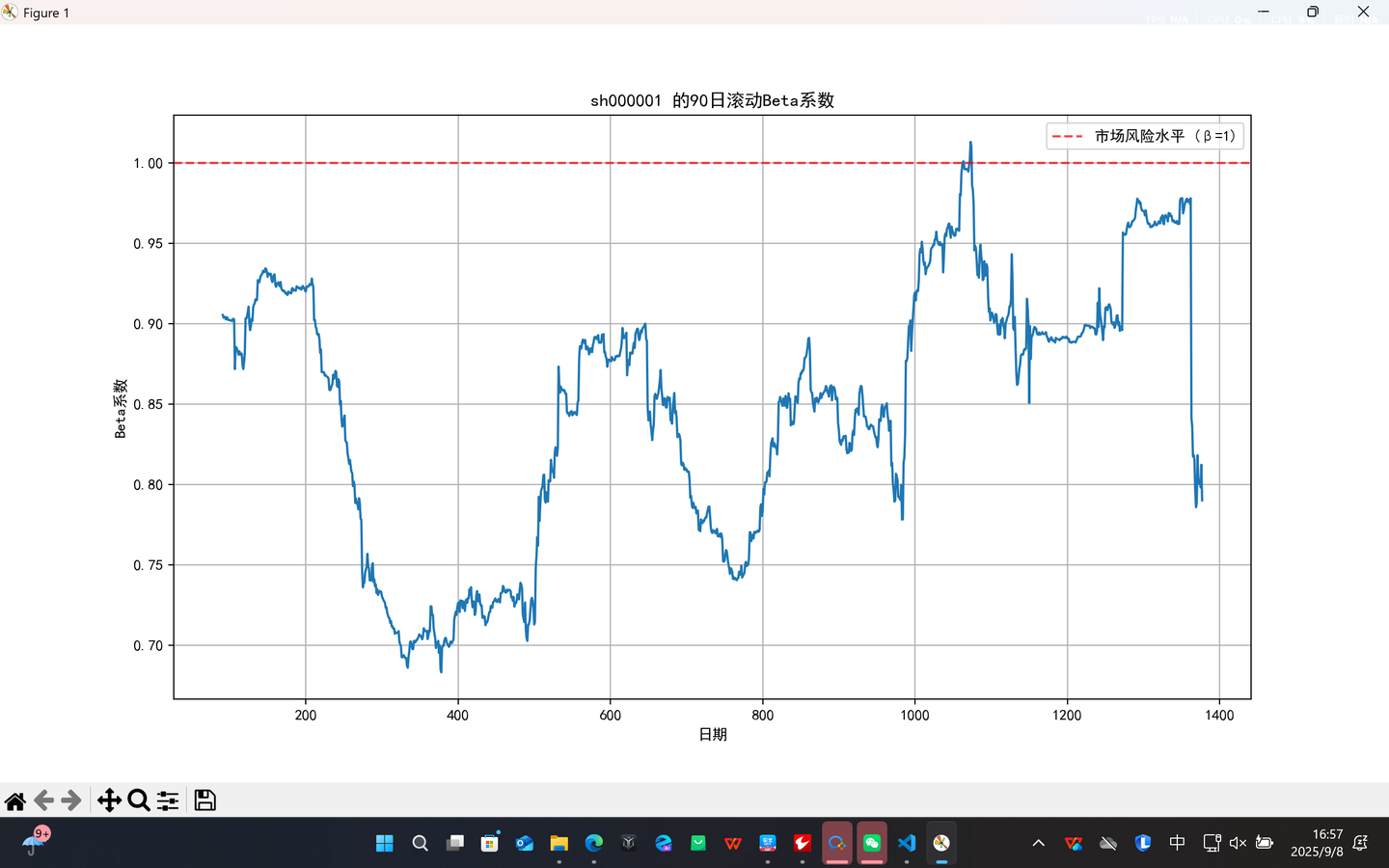
plt.figure(figsize=(12, 6))
rolling_beta.plot()
plt.title(f'{ticker} 的{window}日滚动Beta系数')
plt.ylabel('Beta系数')
plt.xlabel('日期')
plt.grid(True)
plt.axhline(y=1, color='r', linestyle='--', alpha=0.7, label='市场风险水平 (β=1)')
plt.legend()
plt.show()# 输出Beta统计信息
print(f"\nBeta统计信息:")
print(f"平均值: {rolling_beta.mean():.4f}")
print(f"标准差: {rolling_beta.std():.4f}")
print(f"最小值: {rolling_beta.min():.4f}")
print(f"最大值: {rolling_beta.max():.4f}")# 计算投资组合Beta示例
print("\n" + "="*50)
print("投资组合Beta计算示例")
print("="*50)
