TI-92 Plus计算器:高等数学之函数特性判断
1 TI-92 Plus计算器:高等数学之函数特性判断
::: alert-danger
以前高等数学没有学好,一来与自己的资质浅薄有很大的关系,二来与当时的硬件条件也有一定关系,最近在海鲜市场淘了台TI-92 Plus,再翻了翻当年《高等数学》课本后面的习题,发现用TI-92 Plus来理解函数的特性真是太方便了!当年要是有这神器,成绩起码再提10分!
:::
函数的几大特性:
- 函数的有界性
- 函数的单调性
- 函数的奇偶性
- 函数的周期性
习题1:使用描点法作函数y=1x2y=\frac{1}{x^2}y=x21的图形。
解:在函数编辑器中输入y1(x)=1/x^2,切换到作图界面,得到图形如下:
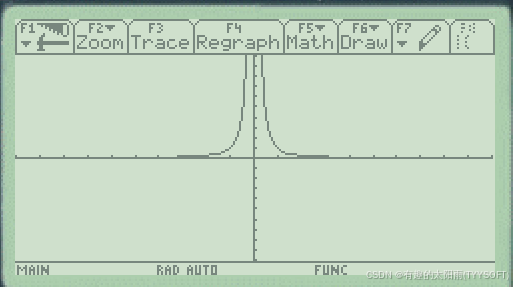
是不是很多马大哈只作了第一象限的图?
习题2:判断函数y=x2(1−x2)y=x^2(1-x^2)y=x2(1−x2)函数的奇偶性
解:在函数编辑器中输入y1(x)=x^2(1-x^2),切换到作图界面,得到图形如下:
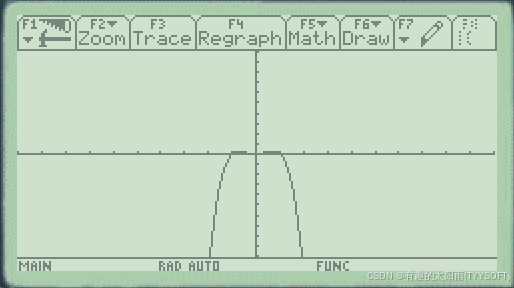
从图形可以看出来,这个函数是偶函数(当然,习题中的作法不能简单的如图,该函数是偶函数,数学是一门严谨的学科)。
使用TI-92 Plus更严谨一点的做法是计算函数的结果(当然,不是使用具体数值)。
步骤1:将a作为常量赋值给x。
步骤2:计算x2(1−x2)x^2(1-x^2)x2(1−x2)的值
步骤3:计算(−x)2[1−(−x)2](-x)^2[1-(-x)^2](−x)2[1−(−x)2]的值
步骤4:比较两次计算结果是否相同,如下图所示:

注:因为x2(1−x2)x^2(1-x^2)x2(1−x2)与(−x)2(1−(−x)2)(-x)^2(1-(-x)^2)(−x)2(1−(−x)2)的值都是−a2(a2−1)-a^2(a^2 -1)−a2(a2−1),y=x2(1−x2)y=x^2(1-x^2)y=x2(1−x2)根据偶函数的定义满足条件,所以是偶函数。
习题3:检查函数y=x2,(−1,0)y=x^2,(-1,0)y=x2,(−1,0)的单调性
解:
⑴,在函数编辑器中输入函数:y1(x)=x^2
⑵,在Window编辑器中输入坐标的区间和刻度,如下图:
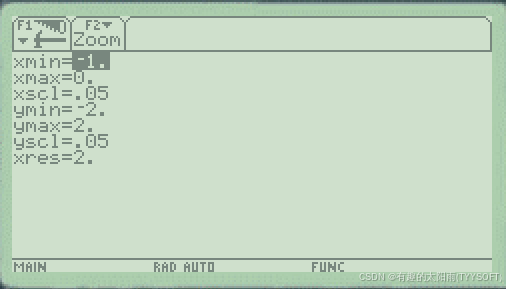
⑶,切换到图形界面,如下图:
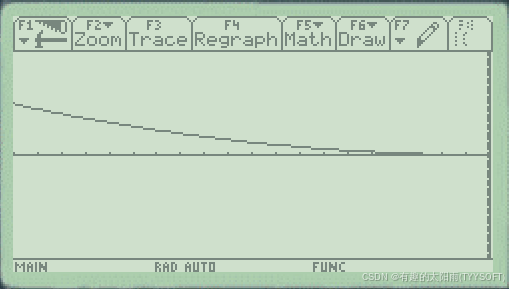
结论:从图中可以看出,y=x2,(−1,0)y=x^2,(-1,0)y=x2,(−1,0)在区间内是单调递减的。
习题4:判断函数y=cos(x−2)y=cos(x-2)y=cos(x−2)是否为周期函数,并指出其周期
解:
⑴,在函数窗口中输入y1(x)=cos(x−2)y1(x)=cos(x-2)y1(x)=cos(x−2)
⑵,在Window窗口中设置刻度,x轴的刻度为π
⑶,切换到图形界面,如下图所示:
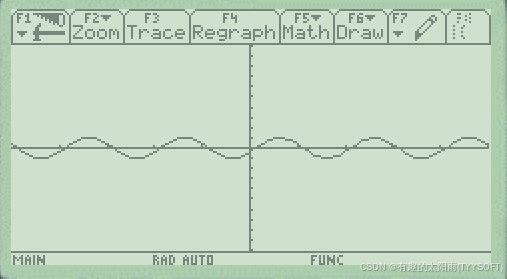
结论:从上图可以看出,该函数是周期性函数,周期为2π 。
作者声明:本文用于记录和分享作者的学习心得,可能有部分文字或示例来自AI平台,如:豆包、DeepSeek(硅基流动)(注册链接)等,由于本人水平有限,难免存在表达错误,欢迎留言交流和指教!
Copyright © 2022~2025 All rights reserved.
