[光学原理与应用-435]:晶体光学 - 晶体的结构-基元/原胞/晶胞/点阵
晶体的结构可通过基元、原胞、晶胞和点阵四个核心概念进行系统描述,它们共同揭示了晶体中原子排列的周期性与对称性规律,具体如下:
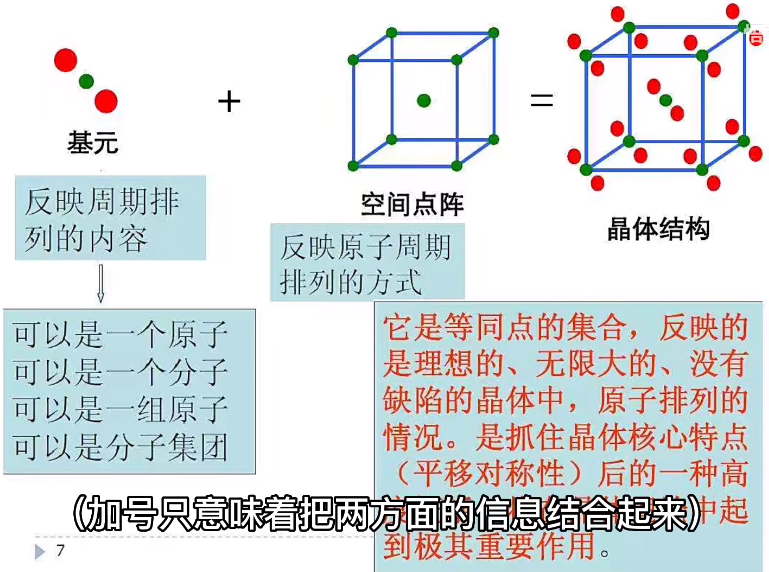
1. 基元(Structure Motif)
- 定义:基元是晶体中重复排列的最小结构单元,可由单个原子、分子、离子或原子团构成。
- 特性:
- 化学等同性:基元内原子种类和数量完全相同。
- 空间等同性:基元在晶体中的环境(如配位数、键长)完全一致。
- 示例:
- 金属铜的基元为单个铜原子。
- 氯化钠(NaCl)的基元为一对Na⁺和Cl⁻离子。
- 金刚石的基元为两个通过共价键连接的碳原子(虽化学组成相同,但空间排列不同,需通过复式格子描述)。
- 数学表达:晶体结构可表示为 晶体结构 = 点阵 + 基元,即基元在空间点阵的每个格点上重复排列形成晶体。
2. 原胞(Primitive Cell)
- 定义:原胞是晶体中体积最小的周期性重复单元,仅包含一个格点(基元中心或原子集团重心)。
- 特性:
- 最小性:原胞是晶格中体积最小的平行六面体,通过三个基矢(a₁, a₂, a₃)沿不共面方向平移可充满整个晶体。
- 平移对称性:原胞的平移操作生成整个晶格。
- 示例:
- 简单立方晶格的原胞为立方体,边长等于晶格常数。
- 面心立方晶格的原胞为菱形十二面体,体积为常规晶胞的1/4。
- 分类:
- Wigner-Seitz原胞:通过作格点与邻近格点连线的垂直平分面,围成的最小区域。它同时考虑了点阵的周期性和对称性,与布拉菲格子具有相同的对称性。
3. 晶胞(Unit Cell)
- 定义:晶胞是能完整反映晶体内部原子排列的最小几何单元,通常为平行六面体。
- 特性:
- 对称性:晶胞需同时体现晶体的周期性和对称性(如镜面对称、旋转对称)。
- 体积多样性:晶胞体积可能是原胞的整数倍(如体心立方晶胞体积为原胞的2倍)。
- 分类:
- 素晶胞(Primitive Unit Cell):仅含一个格点,体积与原胞相同。
- 复晶胞(Conventional Unit Cell):含多个格点(如体心、面心、底心),通过扩大晶胞体积以更直观地反映对称性。
- 示例:
- 氯化钠的晶胞为面心立方结构,含4个Na⁺和4个Cl⁻离子。
- 金刚石的晶胞为面心立方结构,但基元包含两个碳原子,形成复式格子。
4. 点阵(Lattice)
- 定义:点阵是晶体中基元中心或原子集团重心的几何点在空间中的周期性排列,也称为布拉菲格子(Bravais Lattice)。
- 特性:
- 平移对称性:点阵中任意两点通过平移矢量(l = m a₁ + n a₂ + p a₃,m, n, p为整数)可完全复原。
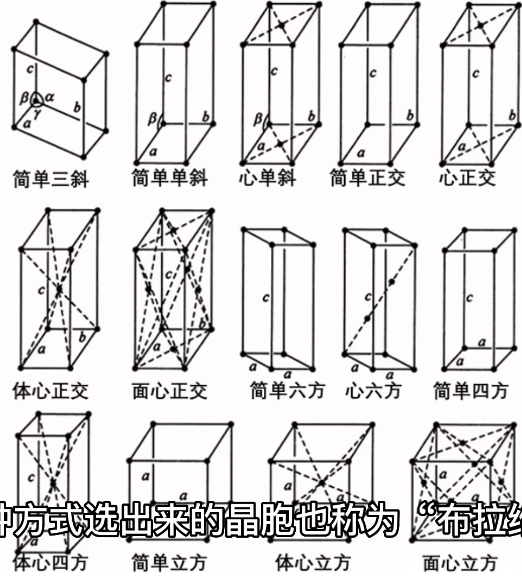
- 对称性分类:根据晶胞参数(a, b, c及夹角α, β, γ),点阵分为7大晶系(三斜、单斜、正交、四方、三方、六方、立方),共14种布拉菲格子。
- 示例:
- 简单立方点阵:格点仅位于立方体顶点。
- 面心立方点阵:格点位于立方体顶点和面心。
- 体心立方点阵:格点位于立方体顶点和体心。
四者关系与区别
| 概念 | 核心特征 | 关系 |
|---|---|---|
| 基元 | 化学与空间等价的最小结构单元 | 基元在点阵的每个格点上重复排列形成晶体。 |
| 原胞 | 体积最小的周期性重复单元 | 原胞的平移操作生成点阵,但可能不反映对称性。 |
| 晶胞 | 反映周期性与对称性的最小几何单元 | 晶胞可能包含多个原胞,用于更直观地描述晶体结构。 |
| 点阵 | 基元中心的几何点周期性排列 | 点阵通过平移操作生成晶体,原胞和晶胞是点阵的具体表现形式。 |
应用与意义
- 材料设计:通过调控基元组成(如合金化)或点阵类型(如相变),可优化材料性能(如强度、导电性)。
- 晶体学分析:X射线衍射通过分析点阵的周期性,确定晶体结构(如DNA双螺旋结构的发现)。
- 纳米技术:原胞和晶胞的尺寸控制(如量子点、纳米线)可实现量子效应的调控。
