当前位置：首页 > news >正文

【机器学习入门】6.2 朴素贝叶斯分类器详解：从理论到西瓜数据集实战

news 2025/9/7 9:35:50

在上一篇文章中，我们学习了贝叶斯决策论的核心思想 —— 用 “新证据更新初始判断” 来计算后验概率，进而做出最优决策。但在实际的分类任务中，特征往往不止一个（比如判断西瓜好坏，需要看色泽、根蒂、敲声等多个特征），直接计算多特征的联合概率会非常复杂。这时候，朴素贝叶斯分类器就登场了 —— 它通过一个 “朴素” 的假设，把复杂的计算简化，成为机器学习中入门级且实用的分类算法。

今天我们就从 “朴素” 的含义入手，一步步拆解朴素贝叶斯的原理、流程，最后用经典的西瓜数据集实战，帮刚入门的同学彻底搞懂这个算法。

1. 为什么需要 “朴素” 贝叶斯？先搞懂核心假设

贝叶斯决策论的核心是计算 “待分类项属于某个类别的后验概率”，公式是：

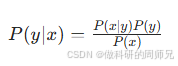
其中 x 是待分类项的所有特征（比如西瓜的色泽、根蒂、敲声等），y 是类别（比如 “好瓜” 或 “坏瓜”）。

问题来了：如果 x 有多个特征（比如 6 个），计算 P(x|y)（类别为 y 时，所有特征同时出现的概率）会非常麻烦。比如要计算 “好瓜类别下，色泽 = 青绿且根蒂 = 蜷缩且敲声 = 浊响” 的概率，需要统计 “既是好瓜、又青绿、又蜷缩、又浊响” 的样本数，若特征多或样本少，很可能统计不到，导致概率为 0。

为了解决这个问题，朴素贝叶斯做了一个关键假设 —— 特征之间条件独立。 “条件独立” 的通俗理解：在已知类别 y 的前提下，某个特征的取值不会影响其他特征的取值。比如对 “好瓜” 来说，“色泽是青绿” 和 “根蒂是蜷缩” 这两个事件互不干扰，不会因为色泽是青绿，根蒂就更可能蜷缩。

这就是 “朴素”（Naive）的由来 —— 用一个简单的独立假设，换来了计算上的巨大便利，让算法能快速落地。

2. 朴素贝叶斯的核心思想：选 “概率最大” 的类别

朴素贝叶斯的分类逻辑非常直接，一句话就能概括：

举个生活中的例子理解：你在街上看到一个黑人，猜他来自哪里。此时 “特征” 是 “肤色 = 黑”，“类别” 是 “非洲人”“美洲人”“亚洲人”。根据统计，“非洲人” 类别中 “肤色 = 黑” 的概率（P (黑 | 非洲人)）很高，且 “非洲人” 的总比例（P (非洲人)）也高，所以 “P (非洲人)×P (黑 | 非洲人)” 会比其他类别大，因此我们更可能猜他来自非洲 —— 这就是朴素贝叶斯的核心逻辑。

3. 朴素贝叶斯分类的正式定义与关键步骤

为了让大家更清晰地理解，我们先给出朴素贝叶斯分类的正式定义，再拆解成可执行的步骤。

3.1 正式定义

假设我们要解决一个二分类或多分类问题：

3.2 三大核心步骤

朴素贝叶斯的实现分为 “准备工作”“训练阶段”“应用阶段” 三大步骤，每个步骤的目标和操作都很明确，入门同学可以直接套用。

步骤 1：准备工作（数据预处理）

确定特征属性：明确待分类问题的特征有哪些，以及每个特征的取值范围。比如西瓜问题的特征的：
- 色泽：{青绿，乌黑，浅白}
- 根蒂：{蜷缩，稍蜷，硬挺}
- 敲声：{浊响，沉闷，清脆}
- 纹理：{清晰，稍糊，模糊}
- 脐部：{凹陷，稍凹，平坦}
- 触感：{硬滑，软粘}
确定类别：明确要划分的类别，比如西瓜的 “好瓜” 和 “坏瓜”。
获取训练样本：收集带有 “特征 + 类别” 标签的数据，比如 17 个已知 “好瓜 / 坏瓜” 的西瓜样本（即西瓜数据集 2.0）。

步骤 2：训练阶段（计算概率）

训练的核心是从训练样本中统计出两个关键概率：

步骤 3：应用阶段（分类预测）

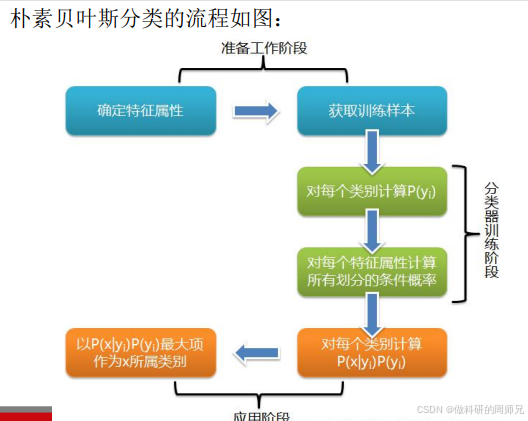
4. 实战：用西瓜数据集训练朴素贝叶斯分类器

光看理论不够，我们用经典的 “西瓜数据集 2.0” 做实战，完整走一遍 “训练→预测” 流程，帮大家把每个步骤吃透。

4.1 实战准备：明确数据与目标

训练样本：17 个西瓜，其中 “好瓜 = 是”8 个，“好瓜 = 否”9 个（特征包括色泽、根蒂、敲声、纹理、脐部、触感）；
测试样本：“测 1”，特征为：色泽 = 青绿、根蒂 = 蜷缩、敲声 = 浊响、纹理 = 清晰、脐部 = 凹陷、触感 = 硬滑；
目标：判断 “测 1” 是好瓜还是坏瓜。

4.2 步骤 1：计算类别先验概率 \(P(y)\)

根据训练样本统计：

4.3 步骤 2：计算关键的类别条件概率 P(xi|y)

我们只需要计算 “测 1” 的特征对应的条件概率（其他特征取值暂时用不上），结果如下：

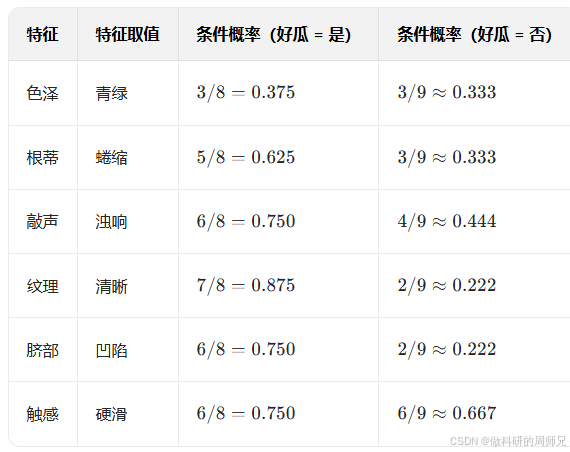
4.4 步骤 3：计算每个类别的 “分子值” 并比较

5. 入门必知：朴素贝叶斯的关键注意点

刚入门的同学在使用朴素贝叶斯时，容易遇到两个问题，这里提前说明，帮大家避坑：

5.2 问题 2：特征是连续值怎么办？（高斯朴素贝叶斯）

我们之前用的西瓜数据集是 “离散特征”（比如色泽、根蒂的取值都是固定的类别），但现实中很多特征是连续值（比如西瓜的重量、含糖量）。此时无法用 “频率” 计算条件概率，需要假设特征服从某种概率分布（比如正态分布）。

解决方法：高斯朴素贝叶斯（Gaussian Naive Bayes）。假设每个类别下的连续特征服从正态分布，通过训练样本计算该分布的均值和方差，再用正态分布的概率密度函数计算条件概率。

6. 朴素贝叶斯的应用场景与优缺点

理解了原理和实战后，我们再看看朴素贝叶斯的实际价值，帮大家知道 “什么时候该用它”：

6.1 核心应用场景

朴素贝叶斯虽然简单，但在很多场景下效果很好，尤其是：

文本分类：比如垃圾邮件识别（特征：邮件关键词，类别：垃圾 / 正常）、情感分析（特征：文本词汇，类别：正面 / 负面）；
小样本分类：由于计算依赖频率统计，小样本数据也能快速训练；
实时分类：计算速度快，适合对响应时间要求高的场景（比如实时新闻分类）。

6.2 优缺点总结

优点	缺点
原理简单，容易理解和实现	特征独立假设在现实中往往不成立（比如文本中 “国王” 和 “皇后” 相关）
计算速度快，不需要复杂的迭代训练	对特征相关性敏感，若特征高度相关，会导致概率计算偏差
对小样本数据友好，泛化能力较强	对异常值敏感，异常值会影响均值、方差等参数的估计