自适应滤波器：Ch1 正交性原理-＞维纳-霍夫方程

维纳滤波器

维纳滤波器是自适应滤波器下的一类线性最优离散滤波器。有别于传统意义的滤波器设计，维纳滤波器一般用于复值随机过程，其滤波器的输出表征的是一种估计。

维纳滤波器一般采用FIR形式，如下所示：

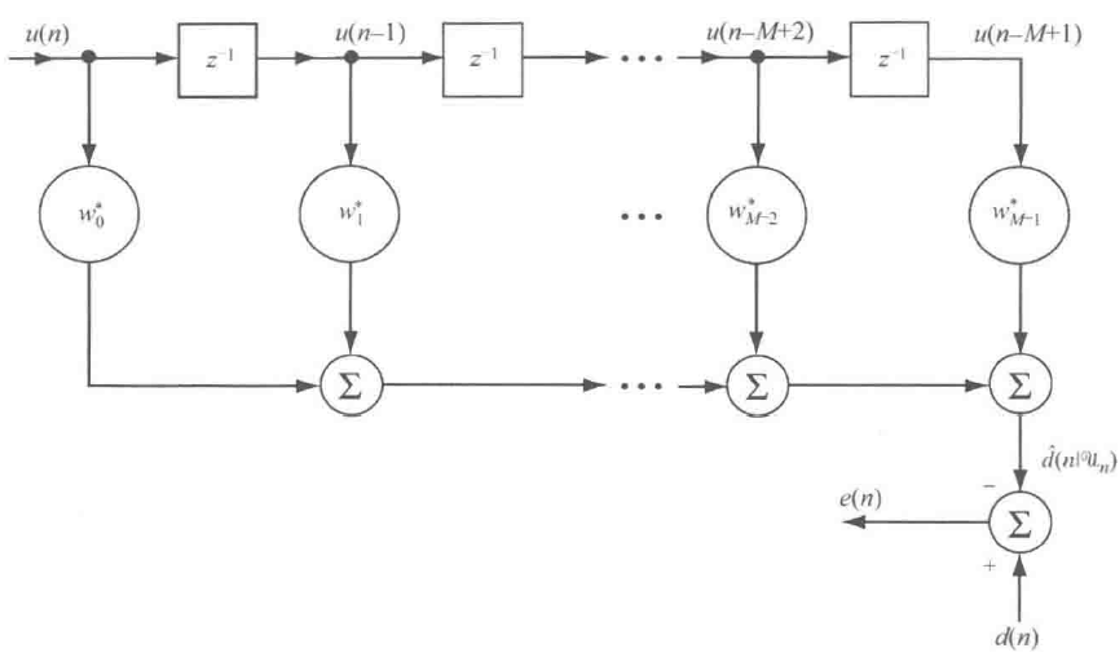
由上图可得，维纳滤波器的输出（是一个估计值）被定义为$\hat{d}(n)$，也就是n时刻的估计。即
$$\hat{d}(n)=\sum _{k=0}^{M-1}{w^{\ast }}_k\ast u(n-k)$$

该滤波器具备

1. M级输入，$u(n-k),k=0,1,2,3,\dots ,M-1$

2. M级系数，${w^{\ast }}_k,k=0,1,2,3,\dots ,M-1$

3. 输出$\hat{d}(n)$，其上标^表示该值为估计输出（不带上标^的表示期望输出）。

估计误差被定义为期望输出与估计输出的差值，即
$$e(n)=d(n)-\hat{d}(n)$$

注意：

1. 这里将FIR的级数限制为M，而不是无穷，是因为这里仅考虑有限的FIR结构

2. 这里${w^{\ast }}_k$的星号指的是共轭复数。这里的$u(n-k)$和${w^{\ast }}_k$都是复数。

在滤波器优化设计过程中，可以考虑采用某种最小代价函数或者某个性能指标来衡量，一般有下列几种选择：

1. 估计误差的均方值

2. 估计误差绝对值的期望值

3. 估计误差绝对值的三阶或高阶期望值

选项1在数学上更加容易处理，而且选择均方误差准则导致滤波器冲激响应未知系数代价函数的二阶相关性，同时该代价函数有一个独特的最小值能唯一的定义滤波器的统计优化设计。故维纳滤波器所用的代价函数是估计误差的均方值，即
$$J=E[e(n)\ast e^{\ast }(n)]=E[|e(n){|}^2]$$

上式中符号$E$表示期望（expectation）

而代价函数J的最小值，就是维纳滤波器的最优解。因此维纳滤波器的设计，就是求取代价函数J的最小值时的滤波器系数（LMMSE，线性最小均方误差估计器）。

关于维纳滤波器的最优解，下面将会从两个角度分别证明：一个是从正交性原理出发，另一个是从误差曲面出发。两者的结果是等价的，下面分别给出证明。

正交性原理

正交性原理->维纳-霍夫方程

将估计误差$e(n)$的表达式代入到代价函数J中后进一步得到
$$J=E[(d(n)-\hat{d}(n))\ast (d^{\ast }(n)-{\hat{d}}^{\ast }(n))]=E\left[\left(d(n)-\sum _{k=0}^{M-1}u(n-k)\ast {w^{\ast }}_k\right)\ast \left(d^{\ast }(n)-\sum _{i=0}^{M-1}{u}^{\ast }(n-i)\ast w_i\right)\right]$$

由于滤波器系数$w_k$和${w^{\ast }}_k$是复数，它可以进一步的被表示为实数和虚数的和，即
$$w_k=a_k+j\ast b_k$$
$${w^{\ast }}_k=a_k-j\ast b_k$$

定义梯度算子${\nabla }_k$（即对第k个滤波器系数的实数部分和虚数部分分别求偏导），即
$${\nabla }_k=\frac{\partial }{\partial a_k}+j\frac{\partial }{\partial b_k}$$

使得所有的梯度算子（k=0,1,…M-1）作用于J后都为0，也就是一阶导为0，可得最小J
$${\nabla }_{k}J=\frac{\partial J}{\partial a_k}+j\frac{\partial J}{\partial b_k}=0$$

下面详细计算梯度算子
$${\nabla }_{k}J=\frac{\partial J}{\partial a_k}+j\frac{\partial J}{\partial b_k}=E\left[\frac{\partial \left[e(n)\ast e^{\ast }(n)\right]}{\partial a_k}\right]+jE\left[\frac{\partial \left[e(n)\ast e^{\ast }(n)\right]}{\partial b_k}\right]=E\left[\frac{\partial e(n)}{\partial a_k}\ast e^{\ast }(n)+\frac{\partial e^{\ast }(n)}{\partial a_k}\ast e(n)+j\frac{\partial e(n)}{\partial b_k}\ast e^{\ast }(n)+j\frac{\partial e^{\ast }(n)}{\partial b_k}\ast e(n)\right]$$

偏微分的计算过程都是类似的，下面将详细计算第一个部分，即
$$\frac{\partial e(n)}{\partial a_k}=\frac{\partial \left(d(n)-\hat{d}(n)\right)}{\partial a_k}=-\frac{\partial \hat{d}(n)}{\partial a_k}=-\frac{\partial \left({\sum }_{k=0}^{M-1}u(n-k)\ast {w^{\ast }}_k\right)}{\partial a_k}=-\frac{\partial \left(u(n-k)\ast {w^{\ast }}_k\right)}{\partial a_k}=-\frac{\partial \left(u(n-k)\ast \left(a_k-j\ast b_k\right)\right)}{\partial a_k}=-u(n-k)$$

同理可得下面所有的偏微分结果，如下
$$\frac{\partial e(n)}{\partial a_k}=-u(n-k)\frac{\partial e(n)}{\partial b_k}=j\ast u(n-k)\frac{\partial e^{\ast }(n)}{\partial a_k}=-u^{\ast }(n-k)\frac{\partial e^{\ast }(n)}{\partial b_k}=-j\ast u^{\ast }(n-k)$$

将这四个偏微分结果全都代入，可得
$${\nabla }_{k}J=E\left[-u(n-k)\ast e^{\ast }(n)-u^{\ast }(n-k)\ast e(n)-u(n-k)\ast e^{\ast }(n)+u^{\ast }(n-k)\ast e(n)\right]=E\left[-u(n-k)\ast e^{\ast }(n)-u(n-k)\ast e^{\ast }(n)\right]=-2\ast E\left[u(n-k)\ast e^{\ast }(n)\right]$$

重新整理一下得到
$${\nabla }_{k}J=-2\ast E\left[u(n-k)\ast e^{\ast }(n)\right]$$

当滤波器工作在最优条件下时,J将达到最小值，此时：

1. 最优条件时 ${\nabla }_{k}J$ 应当为0.

2. 最优条件时滤波器输出的估计值 $\hat{d}(n)$
   被重新定义为最优估计${\hat{d}}_0(n)$，下标0代表最优解。

3. 最优条件时估计误差 $e(n)$ 也被重新定义为最优估计误差$e_0(n)$
   ，下标0代表最优解。
   $$e(n)=d(n)-\hat{d}(n)\stackrel{J最小}{\to }d(n)-{\hat{d}}_0(n)=e_0(n)$$

因此当滤波器工作在最优条件时可得正交性原理，即
$$E\left[u(n-k)\ast {e^{\ast }}_0(n)\right]=0，k=0,1,2,3,\dots \dots M-1$$

正交性原理：

使得滤波器工作在最优解，或者使得代价函数J获得最小值的充要条件是：在n时刻的估计误差$e(n)$正交与滤波器的任意一个输入$u(n-k),k=0,1,2,3,\dots M-1$

进一步查看滤波器输出的估计值$\hat{d}(n)$与估计误差$e(n)$的相关特性：
$$E\left[\hat{d}(n)\ast e^{\ast }(n)\right]=E\left[\sum _{k=0}^{M-1}{w^{\ast }}_k\ast u(n-k)\ast e^{\ast }(n)\right]=\sum _{k=0}^{M-1}{w^{\ast }}_k\ast E[u(n-k)\ast e^{\ast }(n)]$$

当满足正交条件时，即
$$E\left[u(n-k)\ast {e^{\ast }}_0(n)\right]=0，k=0,1,2,3,\dots \dots M-1$$
$$e(n)=d(n)-\hat{d}(n)\stackrel{J最小}{\to }d(n)-{\hat{d}}_0(n)=e_0(n)$$

上式进一步变为如下所示，其中${w^{\ast }}_{0k}$表示最优条件下的滤波器系数。
$$E\left[\hat{d}(n)\ast e^{\ast }(n)\right]\stackrel{J最小}{\Rightarrow }\sum _{k=0}^{M-1}{w^{\ast }}_{0k}\ast E[u(n-k)\ast {e^{\ast }}_0(n)]=0$$

重新整理一下可得正交性原理的推论：在最优条件下，滤波器的输出估计值$\hat{d}(n)$正交与估计误差$e(n)$，即
$$E\left[\hat{d}(n)\ast e^{\ast }(n)\right]=0$$

正交原理总结：

1. 滤波器工作在最优条件下，期望响应的估值用${\hat{d}}_0(n)$表示，相应的估计误差$e_0(n)$与他们互相正交
   $$E\left[{\hat{d}}_0(n)\ast {e^{\ast }}_0(n)\right]=0$$

2. 滤波器工作在最优条件下，估计误差$e_0(n)$正交与n时刻进入期望响应估计的每一个输入样值

$$E[u(n-k)\ast {e^{\ast }}_0(n)]=0$$
$$k=0,1,2,3,\dots \dots M-1$$

接下来利用正交原理以及推论进一步推导维纳滤波器及其最优解。

同时将$$E\left[u(n-k)\ast {e^{\ast }}_0(n)\right]=0，k=0,1,2,3,\dots \dots M-1$$
$$e(n)=d(n)-\hat{d}(n)\stackrel{J最小}{\to }d(n)-{\hat{d}}_0(n)=e_0(n)$$
代入正交公式$E[u(n-k)\ast {e^{\ast }}_0(n)]=0$，可得：
$$E\left[u(n-k)\ast {e^{\ast }}_0(n)\right]=E\left[u(n-k)\ast \left(d^{\ast }(n)-{{\hat{d}}_0}^{\ast }(n)\right)\right]=E\left[u(n-k)\ast \left(d^{\ast }(n)-\sum _{i=o}^{M-1}{u}^{\ast }(n-i)\ast w_{0i}\right)\right]=0$$

展开并整理可继续得到
$$E\left[u(n-k)\ast d^{\ast }(n)\right]=\sum _{i=o}^{M-1}{w}_{0i}\ast E[u(n-k)u^{\ast }(n-i)]$$

继续定义自相关函数
$$r(i-k)=E\left[u(n-k)u^{\ast }(n-i)\right]$$

互相关函数
$$p(-k)=E\left[u(n-k)\ast d^{\ast }(n)\right]$$

利用这两个相关函数，进一步得到了最优滤波器的另一个充要条件，也就是维纳-霍夫方程
$$\sum _{i=0}^{M-1}{w}_{0i}\ast r(i-k)=p(-k)，k=0,1,2,3,\dots \dots M-1$$

其中 $r(i-k)$ 代表相隔i-k个延迟的滤波器输入的自相关函数（$u(n-k)$
and $u(n-i)$)

其中 $p(-k)$代表了滤波器输入与期望输出相隔-k个延迟的互相关（$u(n-k)$ and $d(n)$)

由此我们从正交性原理出发，结合实际的自相关函数和互相关函数，我们得到了滤波器的最优解是满足维纳-霍夫方程的，也就得到了滤波器的再最优条件下的系数的取值$w_{0i}$

为了方便求解维纳-霍夫方程，下面采用矩阵的形式。

首先定义$u(n)$的自相关矩阵R，它是一个M X M的方矩阵。
$$R=E[\overrightarrow{u}\ast {\overrightarrow{u}}^H]$$

其中$\overrightarrow{u}$和${\overrightarrow{u}}^H$的定义如下，其中上标H代表取厄米共轭，即转置+共轭
$$\overrightarrow{u}=\left[\begin{array}{c}u(n)\\ u(n-1)\\ u(n-2)\\ ...\\ u(n-M+1)\end{array}\right],{\overrightarrow{u}}^H=\left[\begin{array}{ccccc}{u}^{\ast }(n)& u^{\ast }(n-1)& u^{\ast }(n-2)& ...& u^{\ast }(n-M+1)\end{array}\right]$$

因此可得
$$R=\left[\begin{array}{ccccc}r(0)& r(1)& r(2)& ...& r(M-1)\\ r^{\ast }(1)& r(0)& r(1)& ...& r(M-2)\\ r^{\ast }(2)& r^{\ast }(1)& r(0)& ...& r(M-3)\\ ...& ...& ...& ...& ...\\ r^{\ast }(M-1)& r^{\ast }(M-2)& r^{\ast }(M-3)& ...& r(0)\end{array}\right]$$

矩阵各个元素计算举例
$$r(0)=E\left[u(n)\ast u^{\ast }(n)\right]=E\left[u(n-1)\ast u^{\ast }(n-1)\right]=E\left[u(n-M+1)\ast u^{\ast }(n-M+1)\right]r(1)=E[u(n)\ast u^{\ast }(n-1)]=E[u(n-1)\ast u^{\ast }(n-2)]=E[u(n-M+2)\ast u^{\ast }(n-M+1)]r^{\ast }(1)=(r(1){)}^{\ast }=(E[u(n)\ast u^{\ast }(n-1)]{)}^{\ast }=E[u(n-1)\ast u^{\ast }(n)]=E[u(n-M+1)\ast u^{\ast }(n-M+2)]$$

接下来定义互相关矩阵P
$$P=E\left[u\ast d^{\ast }(n)\right]=E\left[\left[\begin{array}{c}u(n)\\ u(n-1)\\ u(n-2)\\ \dots \\ u(n-M+1)\end{array}\right]\ast d^{\ast }(n)\right]=\left[\begin{array}{c}p(0)\\ p(-1)\\ p(-2)\\ ...\\ p(-M+1)\end{array}\right]$$

矩阵各个元素计算举例
$$p(0)=E\left[u(n)\ast d^{\ast }(n)\right]p(-1)=E\left[u(n-1)\ast d^{\ast }(n)\right]$$

将P和R代入，即可得到
$$R\ast {\overrightarrow{w}}_0=P$$

其中${\overrightarrow{w}}_0$就是最优条件下的滤波器系数，即
$${\overrightarrow{w}}_0=\left[\begin{array}{c}{w}_{01}\\ \begin{array}{c}{w}_{02}\\ \dots \end{array}\\ w_{0M-1}\end{array}\right]$$

如果R矩阵是非奇异的，可以解出${\overrightarrow{w}}_0$矩阵，即
$${\overrightarrow{w}}_0=R^{-1}\ast P$$

因此为了求取最优条件下的滤波器抽头系数（或者说最优抽头权向量）需要知道两个条件：

1. 输入的自相关函数

2. 输入和期望输出的互相关函数

小结

这一节我们从正交性原理出发，推得维纳霍夫方程。也就是说，满足维纳-霍夫方程就可以使得滤波器工作在最优条件，此时估计误差的均方值最小。

估计误差的均方值J最小

$$\downarrow$$
$${\nabla }_{k}J=0$$

$$\downarrow$$

$$E[u(n-k)\ast {e^{\ast }}_0(n)]=0$$

$$\downarrow$$
$${\overrightarrow{w}}_0=R^{-1}\ast P$$

正交性原理->最小均方误差

接下来利用正交原理来推导估计的均方误差的最小值，即代价函数最小值。

重写最优估计误差$e_0(n)$，期望输出$d(n)$和最优估计值${\hat{d}}_0(n)$三者之间的关系。
$$d(n)-{\hat{d}}_0(n)=e_0(n)$$

也可以写成
$$d(n)={\hat{d}}_0(n)+e_0(n)$$

上式的左右两边分别取方差，左式的方差就是
$$var(d(n))=E[(d(n)-E(d(n)){)}^2]={{\sigma }_d}^2$$

右式的方差就是
$$var({\hat{d}}_0(n)+e_0(n))=E[({\hat{d}}_0(n)+e_0(n)-E[{\hat{d}}_0(n)+e_0(n)]{)}^2]=E[({\hat{d}}_0(n)-E[{\hat{d}}_0(n)]{)}^2]+E[(e_0(n)-E[e_0(n)]{)}^2]-2\ast E\left[\left[{\hat{d}}_0(n)-E[{\hat{d}}_0(n)]\right]\ast \left[{e_0}^{\ast }(n)-E[{e_0}^{\ast }(n)]\right]\right]={{\sigma }_{{\hat{d}}_0}}^2+E[(e_0(n{)}^2]-2\left[E[{\hat{d}}_0(n)\ast {e_0}^{\ast }(n)]-E[{\hat{d}}_0(n)]\ast E[{e_0}^{\ast }(n)]\right]={{\sigma }_{{\hat{d}}_0}}^2+{J\left[E[{\hat{d}}_0(n)\ast {e_0}^{\ast }(n)]-E[{\hat{d}}_0(n)]\ast E[{e_0}^{\ast }(n)]\right]}_{\min }={{\sigma }_{{\hat{d}}_0}}^2+J_{\min }$$

上式在求解过程中用到了：

1. 即输入$u(n)$是0均值的，即$$E\left({\hat{d}}_0(n)\right)=E\left(\sum _{k=0}^{M-1}{w^{\ast }}_k\ast u(n-k)\right)=\sum _{k=0}^{M-1}{w^{\ast }}_k\ast E\left(u(n-k)\right)=0$$

2. 正交原理

$$E[{\hat{d}}_0(n)\ast {e^{\ast }}_0(n)]=0$$

3. 最优估计误差的均方，就是最小的代价函数

$$J_{\min }$$

联立左右两式的方差结果可得
$${{\sigma }_d}^2={{\sigma }_{{\hat{d}}_0}}^2+J_{\min }$$

或者
$$J_{\min }={{\sigma }_d}^2-{{\sigma }_{{\hat{d}}_0}}^2$$

其中 ${\sigma }_d$ 是期望输出的方差，${\sigma }_{{\hat{d}}_0}$是最优估计的方差，$J_{\min }$就是最优估计时的代价函数的最小值

回顾一下，$\hat{d}(n)$ 表示估值，它由FIR滤波器计算得到，形式如下
$$\hat{d}(n)=\sum _{k=0}^{M-1}{w^{\ast }}_k\ast u(n-k)$$

同时引用上面定义的矩阵：
$$\overrightarrow{u}=\left[\begin{array}{c}u(n)\\ u(n-1)\\ u(n-2)\\ ...\\ u(n-M+1)\end{array}\right],\overrightarrow{w}=\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_{M-1}\end{array}\right],{\overrightarrow{w}}^H=\left[\begin{array}{ccccc}{w^{\ast }}_0& {w^{\ast }}_1& {w^{\ast }}_2& ...& {w^{\ast }}_{M-1}\end{array}\right]$$

因此可以将FIR滤波器重新写成

$$\hat{d}(n)=\sum _{k=o}^{M-1}u(n-k)\ast {w^{\ast }}_k=\left[\begin{array}{ccccc}{w^{\ast }}_0& {w^{\ast }}_1& {w^{\ast }}_2& ...& {w^{\ast }}_{M-1}\end{array}\right]\ast \left[\begin{array}{c}u(n)\\ u(n-1)\\ u(n-2)\\ ...\\ u(n-M+1)\end{array}\right]={\overrightarrow{w}}^H\ast \overrightarrow{u}$$

因此估计的均方${{\sigma }_{\hat{d}}}^2$也可以改写如下，其中$E\left(\hat{d}(n)\right)=0$

$${{\sigma }_{\hat{d}}}^2=E\left[{(\hat{d}(n)-E(\hat{d}(n))}^2\right]=E\left[{\left(\hat{d}(n)\right)}^2\right]=E\left[\hat{d}(n){\hat{d}}^{\ast }(n)\right]=E[{\overrightarrow{w}}^H\overrightarrow{u}\ast ({\overrightarrow{w}}^H\overrightarrow{u}{)}^H]=E[{\overrightarrow{w}}^H\ast \overrightarrow{u}\ast {\overrightarrow{u}}^H\ast \overrightarrow{w}]={\overrightarrow{w}}^H\ast E(\overrightarrow{u}\ast {\overrightarrow{u}}^H)\ast \overrightarrow{w}={\overrightarrow{w}}^{H}R\overrightarrow{w}$$

其中R就是之前被定义的自相关函数矩阵
$$R=\left[\begin{array}{ccccc}r(0)& r(1)& r(2)& ...& r(M-1)\\ r^{\ast }(1)& r(0)& r(1)& ...& r(M-2)\\ r^{\ast }(2)& r^{\ast }(1)& r(0)& ...& r(M-3)\\ ...& ...& ...& ...& ...\\ r^{\ast }(M-1)& r^{\ast }(M-2)& r^{\ast }(M-3)& ...& r(0)\end{array}\right]$$

回忆一下之前的矩阵形式的维纳-霍夫方程，也就是说当维纳滤波器工作在最优条件时，最优滤波器系数${\overrightarrow{w}}_0$应当满足下式：
$$R\ast {\overrightarrow{w}}_0=P$$

或者
$${\overrightarrow{w}}_0=R^{-1}\ast P$$

将维纳-霍夫方程代入${{\sigma }_{\hat{d}}}^2$的表达式，可继续得到在最优条件下的${{\sigma }_{{\hat{d}}_0}}^2$转化为：
$${{\sigma }_{{\hat{d}}_0}}^2={{\overrightarrow{w}}_0}^{H}R{\overrightarrow{w}}_0=(({{\overrightarrow{w}}_0}^H(R{\overrightarrow{w}}_0){)}^H{)}^H=((R{\overrightarrow{w}}_0{)}^H\ast {\overrightarrow{w}}_0{)}^H=(P^H\ast {\overrightarrow{w}}_0{)}^H={(P^H{R}^{-1}P)}^H$$

因为${{\sigma }_{{\hat{d}}_0}}^2$一定是实数，而实数的厄米共轭还是自己本身，因此${{\sigma }_{{\hat{d}}_0}}^2$可继续转化为
$${{\sigma }_{{\hat{d}}_0}}^2={\left({{\sigma }_{{\hat{d}}_0}}^2\right)}^H={({\left(P^H{R}^{-1}P\right)}^H)}^H=P^H{R}^{-1}P$$

然后我们得到了最优估计时的代价函数的最小值
$J_{\min }$，或者说最小均方误差
$$J_{\min }={{\sigma }_d}^2-{{\sigma }_{{\hat{d}}_0}}^2={{\sigma }_d}^2-P^H{R}^{-1}P$$

总结，利用正交原理，我们最终得到了最优解条件下的最小均方误差。