最大似然估计：损失函数的底层数学原理

引言

当你第一次看到线性回归时，你是否注意到了作为参数优化关键的损失函数（均方损失），你是否能够理解它的本质和由来。其实，在我第一次接触时，我是感到有些惊讶的，然后试着去强行理解它，而没有想到它的背后其实有一个数学理论作为支撑——最大似然估计。

最大似然估计

最大似然估计（Maximum Likelihood Estimation，MLE）是一种在统计学和机器学习中用于估计模型参数的方法。其核心思想是：在已知观测数据的情况下，寻找使得观测数据出现概率最大的模型参数值。（核心在于概率最大）

似然函数

我们的目的就是把上面的似然函数变成最大。

下面我们将以均方损失和交叉熵损失作为案例进行说明。

均方损失（MSE）：对应 “观测噪声服从高斯分布” 的 MLE

概率假设：模型预测误差服从高斯分布

theta是参数，也就是均值和方差。

构建对数似然函数

最大化对数似然 → 最小化 MSE

结论

均方损失是 “假设回归任务的观测噪声服从高斯分布” 时，最大似然估计的等价损失函数（即负对数似然）。

交叉熵损失：对应 “类别标签服从伯努利 / 多项式分布” 的 MLE

交叉熵损失是分类任务（输出为离散类别概率，如判断图像是猫 / 狗 / 鸟）中最常用的损失函数，分为二分类和多分类两种形式：

以二分类为例（多分类同理，只需将伯努利分布扩展为多项式分布）：

概率假设：类别标签服从伯努利分布

这个函数设计地很巧妙。

构建对数似然函数

最大化对数似然 → 最小化交叉熵

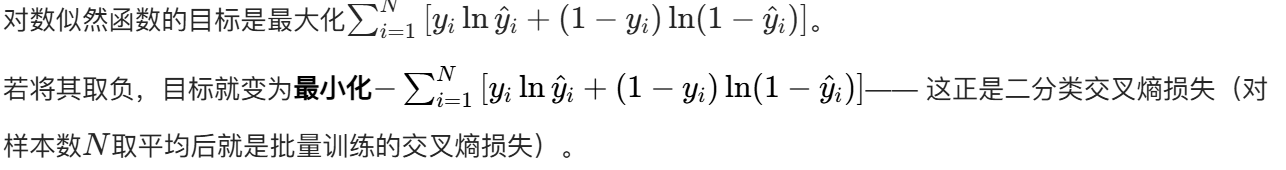
多分类的扩展

结论

交叉熵损失是 “假设分类任务的类别标签服从伯努利分布（二分类）或多项式分布（多分类）” 时，最大似然估计的等价损失函数（即负对数似然）。

核心对比：MSE 与交叉熵的 MLE 本质差异

两种损失函数的根本区别源于对 “标签生成过程” 的概率假设不同，而这种假设又由任务类型（回归 / 分类）决定：

损失函数	适用任务	背后的概率分布假设	MLE 关联（等价性）
均方损失（MSE）	回归（连续输出）	观测噪声～高斯分布	最小化 MSE = 最大化高斯分布下的对数似然
交叉熵损失（CE）	分类（离散类别）	类别标签～伯努利 / 多项式分布	最小化 CE = 最大化伯努利 / 多项式分布下的对数似然

怎么说呢？感觉还是很神奇的，损失函数竟然就这么水灵灵的被推导出来了。