numpy meshgrid 转换成pygimli规则网格

import numpy as np
import pygimli as pg
from scipy.interpolate import griddata

import matplotlib.pyplot as plt

# 1. 生成 NumPy meshgrid
x = np.linspace(0, 10, 11)  # X方向坐标序列
y = np.linspace(0, 5, 6)    # Y方向坐标序列
X, Y = np.meshgrid(x, y)    # 生成网格坐标矩阵:cite[2]

# 2. 提取唯一坐标序列（从meshgrid矩阵中获取）
x_coords = np.unique(X)
y_coords = np.unique(Y)

# 3. 创建 pyGIMLi 规则网格
#    使用 pg.createGrid 并传入提取出的坐标序列
gimli_grid = pg.createGrid(x_coords, y_coords)

# 可视化检查一下生成的网格
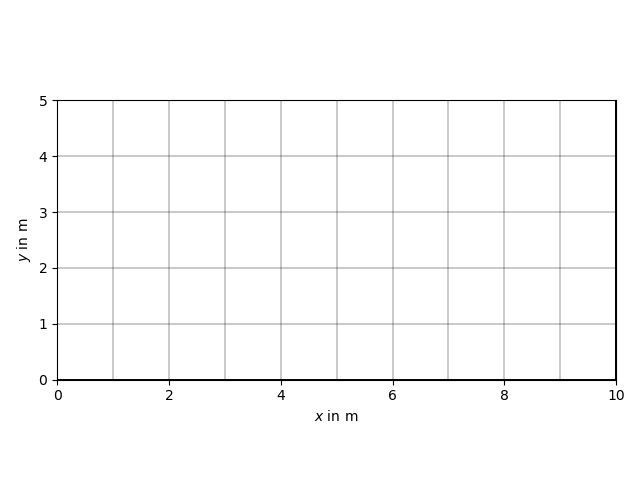
pg.show(gimli_grid)
print("PyGIMLi 网格信息：")
print(f"节点数: {gimli_grid.nodeCount()}")
print(f"单元数: {gimli_grid.cellCount()}")

# 假设我们有一个基于原始 meshgrid 计算得到的函数值
Z_numpy = np.sin(X) * np.cos(Y)
# 获取所有单元中心的坐标，cell_centers 形状应为 (N, 2)
cell_centers = gimli_grid.cellCenters()

# 将单元中心坐标拆分成 x 和 y 分量
x_centers = cell_centers[:, 0]  # 所有x坐标
y_centers = cell_centers[:, 1]  # 所有y坐标
points = np.column_stack((X.ravel(), Y.ravel()))
values = Z_numpy.ravel()
# 现在将 (x_centers, y_centers) 作为元组传递给 griddata
# 这样 xi 就被正确识别为一系列二维点的坐标
gimli_cell_data = griddata(points, values, (x_centers, y_centers), method='nearest')

# 将插值后的数据分配给 pyGIMLi 网格
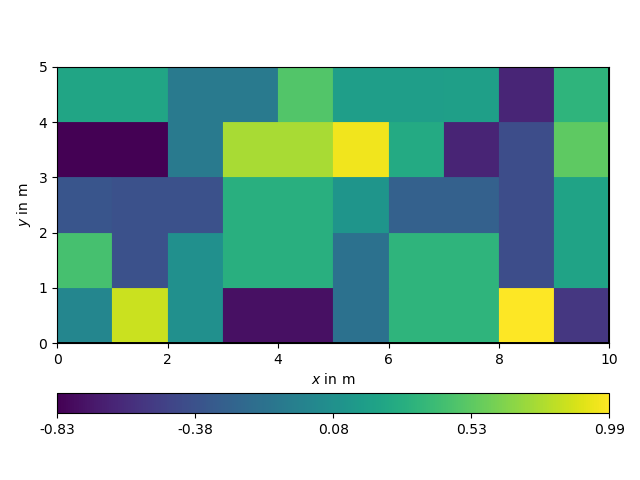
gimli_grid["MyData"] = gimli_cell_data
# 检查分配的数据
print(f"分配给网格的标量场数据: {gimli_grid['MyData']}")

pg.show(gimli_grid,gimli_grid["MyData"])

#将四边形节点转换成pygimli三角网格

import numpy as np
import pygimli as pg
import matplotlib.pyplot as plt

# 假设你已经有四边形网格的节点坐标
# 这里创建一个示例的四边形网格节点
x = np.linspace(0, 10, 6)  # x方向节点
y = np.linspace(0, 5, 4)   # y方向节点
X, Y = np.meshgrid(x, y)   # 创建网格

# 将节点展平并组合成坐标对
points = np.column_stack((X.ravel(), Y.ravel()))

# 方法1: 使用PyGIMLi的createMesh函数直接创建三角网格
# 这会自动对节点进行Delaunay三角剖分
tri_mesh = pg.Mesh(2)  # 创建二维网格

# 添加所有节点到网格中
for pt in points:
tri_mesh.createNode(pt[0], pt[1], 0.0)

# PyGIMLi会自动进行Delaunay三角剖分当你调用createMeshWithPoints时
# 或者使用更直接的方法：
tri_mesh = pg.meshtools.createMesh(points, quality=34, area=0.1)

print(f"三角网格节点数: {tri_mesh.nodeCount()}")
print(f"三角网格单元数: {tri_mesh.cellCount()}")

# 可视化三角网格
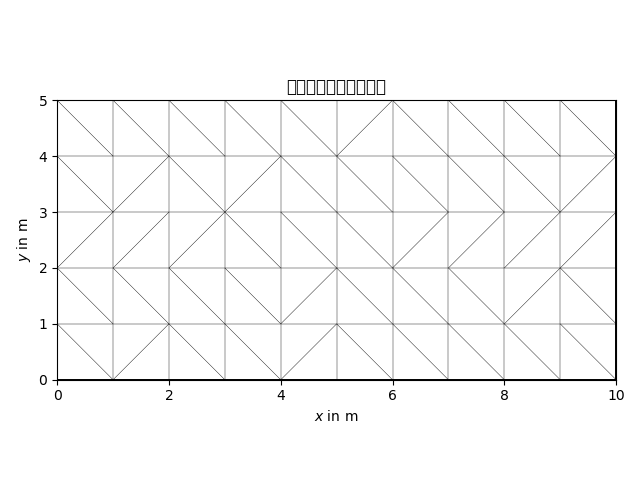
pg.show(tri_mesh)
plt.title("Delaunay三角网格")
plt.show()

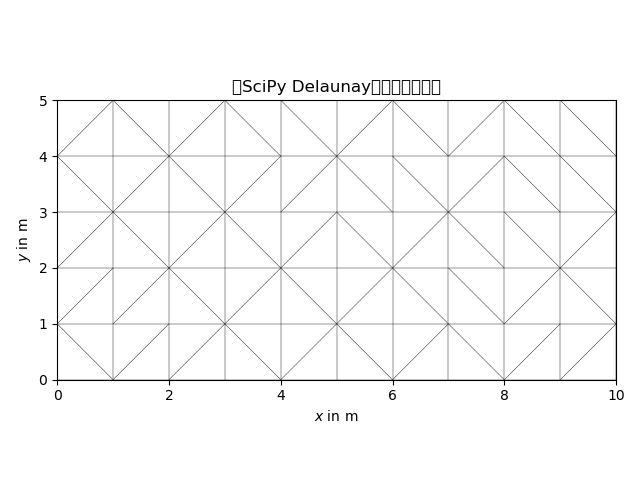
from scipy.spatial import Delaunay

# 使用SciPy进行Delaunay三角剖分
tri = Delaunay(points)

# 创建PyGIMLi网格对象
tri_mesh = pg.Mesh(2)  # 二维网格

# 添加节点
node_ids = []
for pt in points:
node_ids.append(tri_mesh.createNode(pt[0], pt[1], 0.0))

# 添加三角形单元
for simplex in tri.simplices:
# 获取三角形的三个节点
nodes = [node_ids[i] for i in simplex]
# 创建三角形单元
tri_mesh.createTriangle(nodes[0], nodes[1], nodes[2])

print(f"转换后的三角网格信息:")
print(f"节点数: {tri_mesh.nodeCount()}")
print(f"三角形单元数: {tri_mesh.cellCount()}")

# 可视化
pg.show(tri_mesh)
plt.title("从SciPy Delaunay转换的三角网格")
plt.show()

# 创建边界多边形（假设你的四边形网格有特定边界）
polygon = pg.meshtools.createPolygon([
[0, 0],    # 左下角
[10, 0],   # 右下角  
[10, 5],   # 右上角
[0, 5]     # 左上角
], isClosed=True)

# 使用带约束的三角剖分
constrained_mesh = pg.meshtools.createMesh(points, boundary=polygon)

print(f"带约束的三角网格:")
print(f"节点数: {constrained_mesh.nodeCount()}")
print(f"单元数: {constrained_mesh.cellCount()}")

pg.show(constrained_mesh)
plt.title("带边界约束的三角网格")
plt.show()