LeetCode Hot 100 Python (41~50)
二叉树的层序遍历:中等
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
| 示例 | 1 | 2 | 3 |
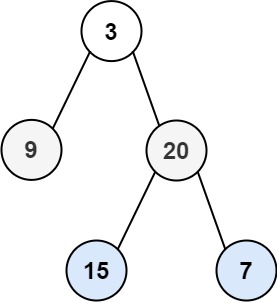
| 输入 | root = [3,9,20,null,null,15,7] | root = [1] | root = [] |
| 输出 | [[3],[9,20],[15,7]] | [[1]] | [] |
|
|
法一:两个数组
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if root is None:return []ans = []cur = [root]while cur:nxt = []vals = []for node in cur:vals.append(node.val)if node.left: nxt.append(node.left)if node.right: nxt.append(node.right)cur = nxtans.append(vals)return ans
法二:一个队列
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if root is None:return []ans = []q = deque([root])while q:vals = []for _ in range(len(q)):node = q.popleft()vals.append(node.val)if node.left: q.append(node.left)if node.right: q.append(node.right)ans.append(vals)return ans
| 时间复杂度 | 空间复杂度 |
| O(n) | O(n) |
| 其中 n 为二叉树的节点个数 | 满二叉树(每一层都填满)最后一层有大约 n/2 个节点,因此数组中最多有 O(n) 个元素,所以空间复杂度是 O(n) 的 |
将有序数组转化为二叉搜索树:简单
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
| 示例 | 1 | 2 |
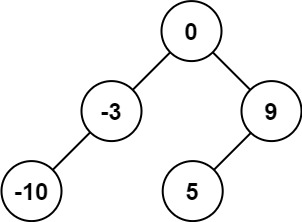
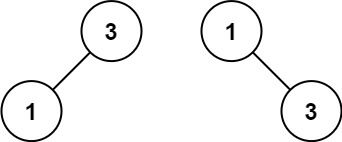
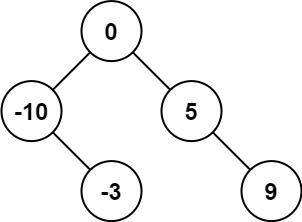
| 输入 | nums = [-10,-3,0,5,9] | nums = [1,3] |
| 输出 | [0,-3,9,-10,null,5] | [3,1] |
|
|
| |
| 解释 | [0,-10,5,null,-3,null,9] 也将被视为正确答案:
| [1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。 |
示例 1 nums=[−10,−3,0,5,9],我们从数组正中间的数 nums[2]=0 开始,把数组一分为二,得到两个小数组:
- 左:[−10,−3]。
- 右:[5,9]。
答案由三部分组成:
- 根节点:节点值为 nums[2]=0。
- 把 nums[2] 左边的 [−10,−3] 转换成一棵平衡二叉搜索树,作为答案的左儿子。这是一个和原问题相似的子问题,可以递归解决。
- 把 nums[2] 右边的 [5,9] 转换成一棵平衡二叉搜索树,作为答案的右儿子。这是一个和原问题相似的子问题,可以递归解决。
递归边界:如果数组长度等于 0,返回空节点。
⚠注意:答案可能不是唯一的。如果 n 是偶数,我们可以取数组正中间左边那个数作为根节点的值,也可以取数组正中间右边那个数作为根节点的值。下面代码取的是正中间右边那个数,即下标为n/2的数(当 n 是偶数时)。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:if not nums:return Nonem = len(nums) // 2left = self.sortedArrayToBST(nums[:m])right = self.sortedArrayToBST(nums[m + 1:])return TreeNode(nums[m], left, right)
| 时间复杂度 | 空间复杂度 |
| O(n) | O(n) |
| 其中 n 是 nums 的长度。每次递归要么返回空节点,要么把 nums 的一个数转成一个节点,所以递归次数是 O(n) 的,所以时间复杂度是 O(n)。需要注意,Python 的第一种写法有切片的复制开销,二叉树的每一层都需要花费 O(n) 的时间,一共有 O(logn) 层,所以时间复杂度是 O(nlogn);第二种写法避免了切片的复制开销,时间复杂度是 O(n) | 如果不计入返回值和切片的空间,那么空间复杂度为 O(logn),即递归栈的开销 |
验证二叉搜索树:中等
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
| 示例 | 1 | 2 |
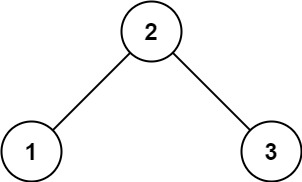
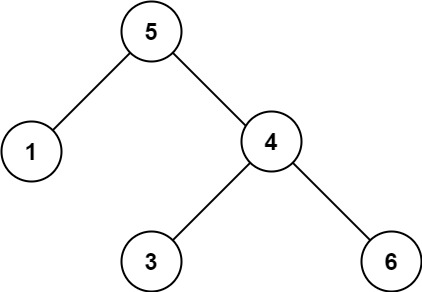
| 输入 | root = [2,1,3] | root = [5,1,4,null,null,3,6] |
| 输出 | True | False |
|
|
| |
| 解释 |