Day19_【机器学习—线性回归 (2)】
三、损失函数简介
线性回归的目标是找到一条最佳拟合直线,而“最佳”是由损失函数定义的,优化过程就是最小化这个损失函数。
损失函数:衡量真实值与预测值之间差异的函数,也叫代价函数、成本函数、目标函数
四、损失函数的数学表达方式
1.最小二乘法
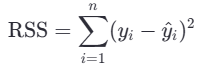
- yi:第 i 个样本的真实值
- y^i:模型预测值
- n:样本数量
2.均方误差MSE
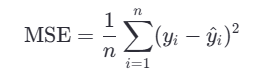
- n:样本数量
- yi:第 i 个样本的真实值
- y^i:模型对第 i 个样本的预测值
- (yi−y^i):预测误差(残差)
3.平均绝对误差MAE
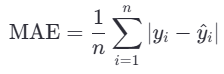
4.MSE vs MAE 简单对比
| 特性 | MSE | MAE |
|---|---|---|
| 是否放大异常值影响 | ✅ 是(平方) | ❌ 否(绝对值) |
| 是否可导处处 | ✅ 是(光滑) | ❌ 否(在0处不可导) |
| 单位 | 目标值的平方 | 与目标值相同 |
| 优化倾向 | 避免大错误 | 平均小误差 |
五、最小化损失函数的方法
1.递归下降法(重点)
1.1.核心思想
梯度:
- 单变量函数中,梯度就是某一点切线斜率(某一点的导数);有方向为函数增长最快的方向
- 多变量函数中,梯度就是某一个点的偏导数;有方向:偏导数分量的向量方向
梯度下降:
是一种通过沿损失函数“最陡下降方向”迭代更新参数,以找到最小值的优化算法。
1.2.数学表达式
梯度下降公式: 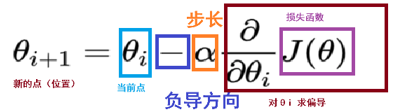
注意 :
1. α: 学习率(步长) ,步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度
- 学习率太小,下降的速度会慢
- 学习率太大:容易造成错过最低点、产生下降过程中的震荡、甚至梯度爆炸.
- 范围:0.001 ~ 0.01
2. 梯度的方向
- 实际就是函数在此点上升最快的方向, 我们需要是下降最快的方向, 所以需要加负号
3.梯度下降的优化过程
- 两次差距小于指定的阈值
- 达到指定的迭代次数
1.3.梯度下降分类
目前最常用的是小批量梯度下降(mini-batch),它结合了SGD的高效和FGD的稳定性,避免了两者的缺点,在实际应用中表现出色。

1.3.1 全梯度下降(F GD)
- 特点:使用全部数据集进行训练。
- 优点:
- 训练过程稳定,收敛到全局最优解的可能性大。
- 缺点:
- 计算速度较慢,尤其是在数据量大的情况下。
- 内存占用高,需要存储所有样本的梯度。
1.3.2 随机梯度下降(SGD)
- 特点:每次只使用一个样本进行迭代更新。
- 优点:
- 简单高效,计算速度快。
- 可以在大数据集上实时更新模型参数。
- 缺点:
- 收敛过程不稳定,容易受到噪声影响。
- 容易陷入局部最优解,特别是在遇到异常值时。
1.3.3 小批量梯度下降(mini-batch)
- 特点:结合了SGD的高效和FGD的稳定性,每次使用一小部分样本进行迭代。
- 优点:
- 避免了FGD运算效率低和SGD收敛效果不稳定的缺点。
- 平衡了计算速度和收敛稳定性,是目前最常用的梯度下降方法。
- 应用:
- 广泛应用于深度学习和大规模机器学习任务中。
1.3.4 随机平均梯度下降(SAG)
- 特点:每轮梯度更新都结合了上一轮的梯度值。
- 优点:
- 利用历史梯度信息,优化速度较快。
- 缺点:
- 训练初期表现不佳,优化速度较慢,因为初始梯度常设为0。
- 内存需求较高,需要存储每个样本的历史梯度。
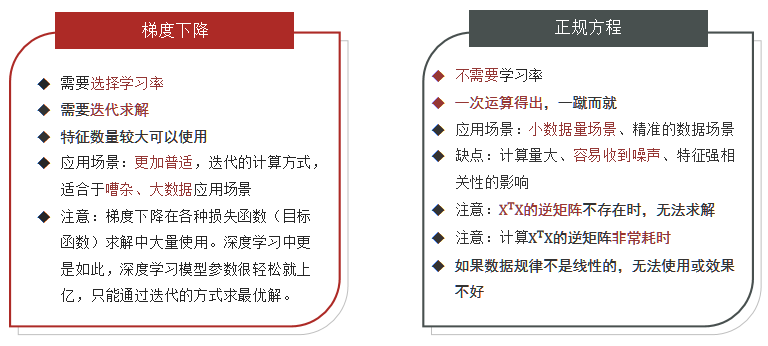
2.正规方程法(了解)
正规方程法的核心思想:利用数学求导+解方程,直接“算出”最优参数。
3.二种方法对比