当前位置：首页 > news >正文

LeetCode 3459.最长 V 形对角线段的长度：记忆化搜索——就一步步试

news 2025/9/1 15:02:28

【LetMeFly】3459.最长 V 形对角线段的长度：记忆化搜索——就一步步试

力扣题目链接：https://leetcode.cn/problems/length-of-longest-v-shaped-diagonal-segment/

给你一个大小为 n x m 的二维整数矩阵 grid，其中每个元素的值为 0、1 或 2。

V 形对角线段 定义如下：

线段从 1 开始。
后续元素按照以下无限序列的模式排列：2, 0, 2, 0, ...。
该线段：
- 起始于某个对角方向（左上到右下、右下到左上、右上到左下或左下到右上）。
- 沿着相同的对角方向继续，保持 序列模式 。
- 在保持 序列模式 的前提下，最多允许 一次顺时针 90 度转向 另一个对角方向。

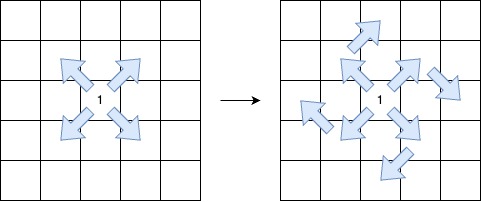
返回最长的 V 形对角线段 的长度。如果不存在有效的线段，则返回 0。

示例 1：

输入： grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 5

解释：

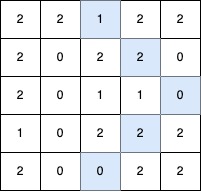
最长的 V 形对角线段长度为 5，路径如下：(0,2) → (1,3) → (2,4)，在 (2,4) 处进行 顺时针 90 度转向 ，继续路径为 (3,3) → (4,2)。

示例 2：

输入： grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 4

解释：

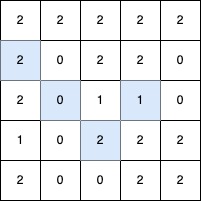
最长的 V 形对角线段长度为 4，路径如下：(2,3) → (3,2)，在 (3,2) 处进行 顺时针 90 度转向 ，继续路径为 (2,1) → (1,0)。

示例 3：

输入： grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

输出： 5

解释：

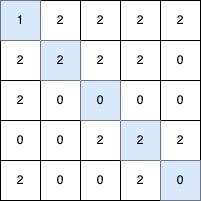
最长的 V 形对角线段长度为 5，路径如下：(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。

示例 4：

输入： grid = [[1]]

输出： 1

解释：

最长的 V 形对角线段长度为 1，路径如下：(0,0)。

提示：

n == grid.length
m == grid[i].length
1 <= n, m <= 500
grid[i][j] 的值为 0、1 或 2。

解题方法：记忆化搜索

解题思路

题目翻译：从一个位置出发沿4个45度倾斜的方向移动，最多右转一次，起点一定是1，经过路径一定是2020...(不能是0202..)，求最长路径是多少。

写一个函数dfs(int i, int j, int d, int times)，代表当前位置坐标为(i, j)、前进方向为d、拐弯了times次的状态下，算上当前位置的最长路径长度。

如果沿当前方向向前走能继续走，那就尝试；如果右转90度能继续走，那就也试试。终止条件：一定会走到走不动为止。

那么，所有grid[i][j] == 1的下标(i, j)，4个方向且times为0的初始状态的到的最大结果即为答案。

然后记得记忆化一下，算过的(i, j, d, times)不要再重复计算一次。

具体方法

实际编码的时候，给定的数据量在使用默认的缓存时可能会TLE或OOM。所以C++和Python要使用数组手动记忆化一下。

如何将(i, j, d, times)映射为一个下标？i * m * 8 + j * 8 + d * 2 + times即可。

剪枝(可选)

有没有可以提前退出的时刻？有，可以维护一个“全局”的最长路径，若当前状态一直往前走无论如何也无法超过历史最优解，索性放弃尝试，及时止损

时空复杂度分析

时间复杂度 $O (mn)$
空间复杂度 $O (mn)$

其实时空复杂度都要乘上一个常数8。

AC代码

C++

/** @Author: LetMeFly* @Date: 2025-08-27 23:08:01* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-08-29 18:50:39*/
#if defined(_WIN32) || defined(__APPLE__)
#include "_[1,2]toVector.h"
#endif#define dbgIJDT(msg) printf("dbg(%s): i == %d && j == %d && d == %d && times == %d\n", msg, i, j, d, times)// 有点卡极限 数据范围似乎不是很好
class Solution {
private:const int directions[4][2] = {{1, 1},    // 0 - ↘️{1, -1},   // 1 - ↙️{-1, -1},  // 2 - ↖️{-1, 1}    // 3 - ↗️};vector<vector<int>> grid;vector<int> cache;int n, m;inline bool canContinue(int i, int j, int ni, int nj) {if (!(ni >= 0 && ni < n && nj >= 0 && nj < m)) {return false;}int thisVal = grid[i][j], nextVal = grid[ni][nj];return (thisVal == 1 && nextVal == 2) || (thisVal != 1 && nextVal != 1 && thisVal != nextVal);}/*>>> 500 * 500250000>>> 500 * 500 * 4 * 22000000>>> 500 * 4 * 24000>>> 4 * 28*/inline int getCacheKey(int i, int j, int d, int times) {return i * 8 * m + j * 8 + d * 2 + times;}int dfs(int i, int j, int d, int times) {int cacheKey = getCacheKey(i, j, d, times);// if (cacheKey == 12018) {//     dbgIJDT("cacheKey=12018");// }if (cache[cacheKey] != -1) {return cache[cacheKey];}int toAdd = 0;int ni = i + directions[d][0], nj = j + directions[d][1];// if (i == 2 && j == 1 && d == 2 && times == 1 || i == 3 && j == 2 && d == 1 && times == 0 || i == 2 && j == 3 && d == 1 && times == 0) {//     dbgIJDT("after cache");// }if (canContinue(i, j, ni, nj)) {toAdd = dfs(ni, nj, d, times);}if (times == 0) {int nd = (d + 1) % 4;int ni = i + directions[nd][0], nj = j + directions[nd][1];if (canContinue(i, j, ni, nj)) {toAdd = max(toAdd, dfs(ni, nj, nd, 1));}}return cache[cacheKey] = 1 + toAdd;}
public:int lenOfVDiagonal(vector<vector<int>>& grid) {this->grid = move(grid);n = this->grid.size(), m = this->grid[0].size();cache.resize(m * n * 8, -1);int ans = 0;for (int i = 0; i < this->n; i++) {for (int j = 0; j < this->grid[i].size(); j++) {if (this->grid[i][j] != 1) {continue;}for (int d = 0; d < 4; d++) {ans = max(ans, dfs(i, j, d, 0));}}}return ans;}
};#if defined(_WIN32) || defined(__APPLE__)
/*
[[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]5
*/
/*
[[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]4
*/
/*
[[1,2,2],[1,0,2]]1 2 2
1 0 22
*/
/*
[[2,2,0,2,0,2,0],[1,2,2,1,0,2,0]]2 2 0 2 0 2 0
1 2 2 1 0 2 02
*/
int main() {string s;while (cin >> s) {vector<vector<int>> v = stringToVectorVector(s);Solution sol;cout << sol.lenOfVDiagonal(v) << endl;}return 0;
}
#endif

AC,64.08%,42.73%

Python

'''
Author: LetMeFly
Date: 2025-08-28 12:54:06
LastEditors: LetMeFly.xyz
LastEditTime: 2025-08-31 19:11:00
'''
from typing import Listclass Solution:directions = [[1, 1],[1, -1],[-1, -1],[-1, 1]]"""canContinue只考虑从(i, j)开始能否沿着方向d走一步"""def canContinue(self, i: int, j: int, d: int) -> bool:ni, nj = i + self.directions[d][0], j + self.directions[d][1]if ni < 0 or ni >= self.n or nj < 0 or nj >= self.m:return Falsenow = self.grid[i][j]next = self.grid[ni][nj]return now == 1 and next == 2 or now != 1 and next != 1 and now != nextdef getCacheKey(self, i: int, j: int, d: int, canChange: bool) -> int:return i * self.m * 8 + j * 8 + d * 2 + canChangedef dfs(self, i: int, j: int, d: int, canChange: bool) -> int:cacheKey = self.getCacheKey(i, j, d, canChange)if self.cache[cacheKey] != -1:return self.cache[cacheKey]then = 0if self.canContinue(i, j, d):then = self.dfs(i + self.directions[d][0], j + self.directions[d][1], d, canChange)if canChange:nd = (d + 1) % 4if self.canContinue(i, j, nd):then = max(then, self.dfs(i + self.directions[nd][0], j + self.directions[nd][1], nd, False))self.cache[cacheKey] = then + 1return then + 1def lenOfVDiagonal(self, grid: List[List[int]]) -> int:self.grid = gridself.n, self.m = len(grid), len(grid[0])self.cache = [-1] * (self.m * self.n * 8)ans = 0for i, line in enumerate(grid):for j, g in enumerate(line):if g != 1:continuefor d in range(4):ans = max(ans, self.dfs(i, j, d, True))return ansif __name__ == '__main__':from functools import cacheclass A:def __init__(self, x):self.x = x@cachedef f(self, y):print("running f...")return self.x + ya1 = A(10)a2 = A(20)print(a1.f(1))  # 运行函数，输出 11print(a1.f(1))  # 命中缓存，直接输出 11print(a2.f(1))  # 不命中缓存，输出21