代码分析之符号执行技术
开篇
今天我们来学习一项在网络安全领域常用的分析技术: 符号执行。
该技术在上个世纪70年代就已经被提出了,经过几十年的发展与优化,目前已经可以说是一项比较成熟的技术了,广泛应用在自动化测试用例生成、程序路径可行性分析和安全漏洞挖掘等领域。
不过不用被它的名字吓到,以为其是某种高大上且艰深难懂的技术,其实它从原理到应用都很好理解。计算机领域存在许多看似高端实则接地气的概念,比如软件设计中的依赖注入、控制反转等等,符号执行也属于这类概念,并不是只有计算机大神们才能掌握的技术。
接下来我们就从符号执行的原理到应用来深入学习下。
原理
符号执行的基本思想是将输入到程序的具体输入数值(比如用户输入、文件数据)用符号来表示(比如α\alphaα、β\betaβ),所谓的符号可以理解为占位符,代表了该输入数据的所有可能的取值。
另外,在符号执行的分析过程中,那些不易或者无法确定取值的变量,往往也使用符号进行表示,并参与后续分析。
然后从头开始遍历每行程序代码,跟踪符号在程序中的传播过程。将每行代码解释为语义对等的对符号的具体操作,比如对符号的加减乘除等操作。
程序中需要处理和计算的变量或者某些"数值",被解释为包含符号与常量的运算表达式,比如变量x=2∗α+12\ast\alpha+12∗α+1。
也就是说,程序的正常执行和符号执行的主要区别是:正常执行时,程序中的变量可以认为被赋予了具体的值。而在符号执行时,变量的值既可以是具体的值,也可以是包含符号的运算表达式。
对于程序中的控制转移语句,比如if、switch-case或while等,符号执行将跳转的条件表示为针对相应符号的多个约束条件。通过求解这些约束条件,可以进一步判断该分支是否可达,这个过程也就是路径可行性分析。
说白了就是解方程,比如对于如下的约束条件:
- 3α+5β=213\alpha+5\beta=213α+5β=21
- 2α−7β=−172\alpha-7\beta=-172α−7β=−17
求解后可得α=2,β=3\alpha=2,\beta=3α=2,β=3,也就是存在输入使该路径可达,反之则该路径不可达。
通过将程序中的输入表示为符号的运算表达式并分析路经条件,可以发现程序的一些特性,而有些特性恰好是漏洞分析所关心的,来达到漏洞挖掘的作用。

形式化说明
一、基础定义
1.符号输入
程序输入变量集合表示为符号变量:
Input={α1,α2,...,αn}Input=\{\alpha_{1},\alpha_{2},...,\alpha_{n}\}Input={α1,α2,...,αn}
2.程序状态
符号执行状态定义为三元组:
State=(σ,pc,loc)State=\left(\sigma,pc,loc\right)State=(σ,pc,loc)
- σ\sigmaσ(符号状态映射):变量到符号表达式的映射函数,即 σ :Var→Expr\sigma\colon Var\rightarrow Exprσ:Var→Expr。例如:σ(x)=2α1+3\sigma\left(x\right)=2\alpha_{1}+3σ(x)=2α1+3表示变量xxx的符号表达式;
- pc(path constraint,路径约束):布尔表达式,记录当前路径的条件分支逻辑组合,初始值为 true;
- loc(location,程序计数器):指向下一条待执行语句的地址或行号;
二、执行规则
符号执行过程通过状态转移函数⇒\Rightarrow⇒描述,状态转移规则如下:
1.赋值语句
对于赋值语句v=ev=ev=e(eee为表达式):
(σ,pc,loc)⇒(σ[v↦σ(e)],pc,loc′)\left(\right.\sigma,pc,loc)\Rightarrow(\sigma[v\mapsto\sigma\left(e)],pc,loc^{\prime}\right)(σ,pc,loc)⇒(σ[v↦σ(e)],pc,loc′)
v↦σ(e)v\mapsto\sigma(e)v↦σ(e)代表变量vvv与表达式eee的符号表达式的映射关系。
更新σ\sigmaσ,增加这个新的映射。loc′loc^{\prime}loc′为下一条语句地址或行号。
2.条件分支
对语句 if (e) S1 else S2:
- Then分支:
(σ,pc,loc)⇒(σ,pc∧σ(e),loc1)(\sigma,pc,loc)\Rightarrow(\sigma,pc\land\sigma(e),loc_1)(σ,pc,loc)⇒(σ,pc∧σ(e),loc1) - Else分支:
(σ,pc,loc)⇒(σ,pc∧¬σ(e),loc2)(\sigma,pc,loc)\Rightarrow(\sigma,pc\land\neg\sigma(e),loc_2)(σ,pc,loc)⇒(σ,pc∧¬σ(e),loc2)
其中σ(e)\sigma(e)σ(e)为条件表达式eee的符号表达式,loc1loc_1loc1和loc2loc_2loc2分别为 S1 和 S2 的入口地址或行号。
3.内存与指针操作
对内存访问 read(addr) 或 write(addr,val):
- 若地址 addr 为符号表达式(如 αi+4),则返回符号化内存值
- 形式化表示为:σ(read(addr))=MEM[σ(addr)]\sigma(read(addr))=MEM[\sigma(addr)]σ(read(addr))=MEM[σ(addr)]
其中MEMMEMMEM为符号化内存映射。
三、约束求解与终止条件
1.路径终止
当执行到达程序结束点、错误点(如assert语句)或任意人为设置的程序点时,当前路径的pc(路径约束)被提交给约束求解器(比如微软的z3):
Solver.check(pc)=(SAT→生成测试输入 UNSAT→路径不可达)Solver.check(pc)=\begin{pmatrix}SAT\rightarrow生成测试输入\ \ UNSAT\rightarrow路径不可达\end{pmatrix}Solver.check(pc)=(SAT→生成测试输入 UNSAT→路径不可达)
求解器输出满足pc的符号的具体值。
2.路径爆炸处理
路径数量随分支数指数增长,需引入剪枝策略:
- 若 pc 包含矛盾(如α>0∧α<0α>0∧α<0α>0∧α<0),终止该路径;
- 动态符号执行中,通过具体值简化约束;
示例说明
接下来,我们用一个示例来说明一下符号执行的基本原理。

符号执行过程:
1.初始状态:σ=x↦α,pc=true,loc=start\sigma={x↦\alpha}, pc=true, loc=startσ=x↦α,pc=true,loc=start。
2.分支语句 if (x>0):
- Then分支:σ1=x↦α,y↦α+1,pc1=(α>0)\sigma1={x\mapsto\alpha,y\mapsto\alpha+1},pc_{1}=(\alpha>0)σ1=x↦α,y↦α+1,pc1=(α>0)。
- Else分支:σ2=x↦α,y↦α−1,pc2=(α⩽0)\sigma2={x\mapsto\alpha,y\mapsto\alpha-1},pc_{2}=(\alpha\leqslant0)σ2=x↦α,y↦α−1,pc2=(α⩽0)
3.断言检查:
- Then分支:需解 pc1∧(α+1=0)pc_1\land(\alpha+1=0)pc1∧(α+1=0)(无解,断言为true)。
- Else分支:需解 pc2∧(α−1=0)pc_2\land(\alpha-1=0)pc2∧(α−1=0)( 无解,断言为true)
可得断言永远不会失败。
应用
这篇文章我们专注于符合执行在安全漏洞挖掘方面的应用,至于其在自动化测试用例生成和其它方面的应用,有兴趣的朋友可以自行搜索相关资料。
使用符号执行进行程序漏洞分析的工作原理如下图所示。
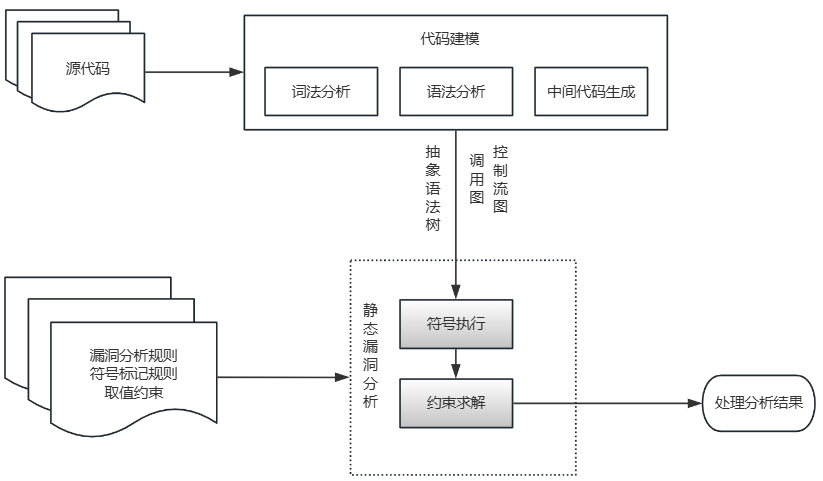
与数据流分析类似,使用符号执行技术进行漏洞分析的系统,常常使用抽象语法树、控制流图、调用图等结构作为程序代码的模型。
漏洞分析规则常常包括符号的标记规则(比如哪些类型的变量需要用符号标记),以及一些在漏洞触发时的变量取值的约束。
静态漏洞分析过程将程序代码模型以及漏洞分析规则作为输人,通过使用符号执行以及约束求解等分析技术查找序中可能存在的漏洞,并将初步的分析结果传递给处理分析结果过程。初步的分析结果经过进一步的处理形成最终的漏洞报告。
1.正向的符号执行
正向的符号执行从某个起始点开始,通过正向遍历程序的路径的方式进行程序漏洞的分析。
在应用正向的符号执行检测程序漏洞时,通过分析路径上的程序语句,不断地将变量的取值表示为符号和常量的表达式,将路径条件表示为符号的约束,同时对符号在程序路径上需要满足的取值约束进行求解,判断路径是否可行,并且在特定的程序点上检查变量的取值是否一定符合程序安全的规定,或者可能满足漏洞存在的条件。
2.逆向的符号分析
符号执行通常是沿着程序路径对程序进行分析,遇到可能引起程序漏洞的程序点,则分析该程序点处是否存在安全问题。
然而,这样的分析过程常常是对程序代码进行全面的分析,缺乏漏洞分析的针对性。而逆向的符号执行分析可以弥补这种不足,有的放矢地进行漏洞分析。
在应用逆向的符号分析方法检测程序漏洞时,通过直接在关键的程序点上分析所关心的变量是否可以满足存在程序漏洞的约束条件,并且通过逆向的分析不断地获取路径条件对所关心变量的取值约束,并计算所关心的变量在当前的约束下是否还满足漏洞的约束条件,进而判断程序漏洞是否真实存在。
分析过程常常在发现所关心变量的取值不再满足漏洞存在的条件或者分析到达程序的入口点终止。
检测程序漏洞
应用符号执行技术,程序中的变量的取值可以被表示为符号和常量组成的计算表达式,而一些程序漏洞可以表现为某些相关变量的取值不满足相应的约束。
这里最具代表性的就是检测C语言程序中的缓冲区溢出漏洞。以下面的linux内核漏洞代码为例:
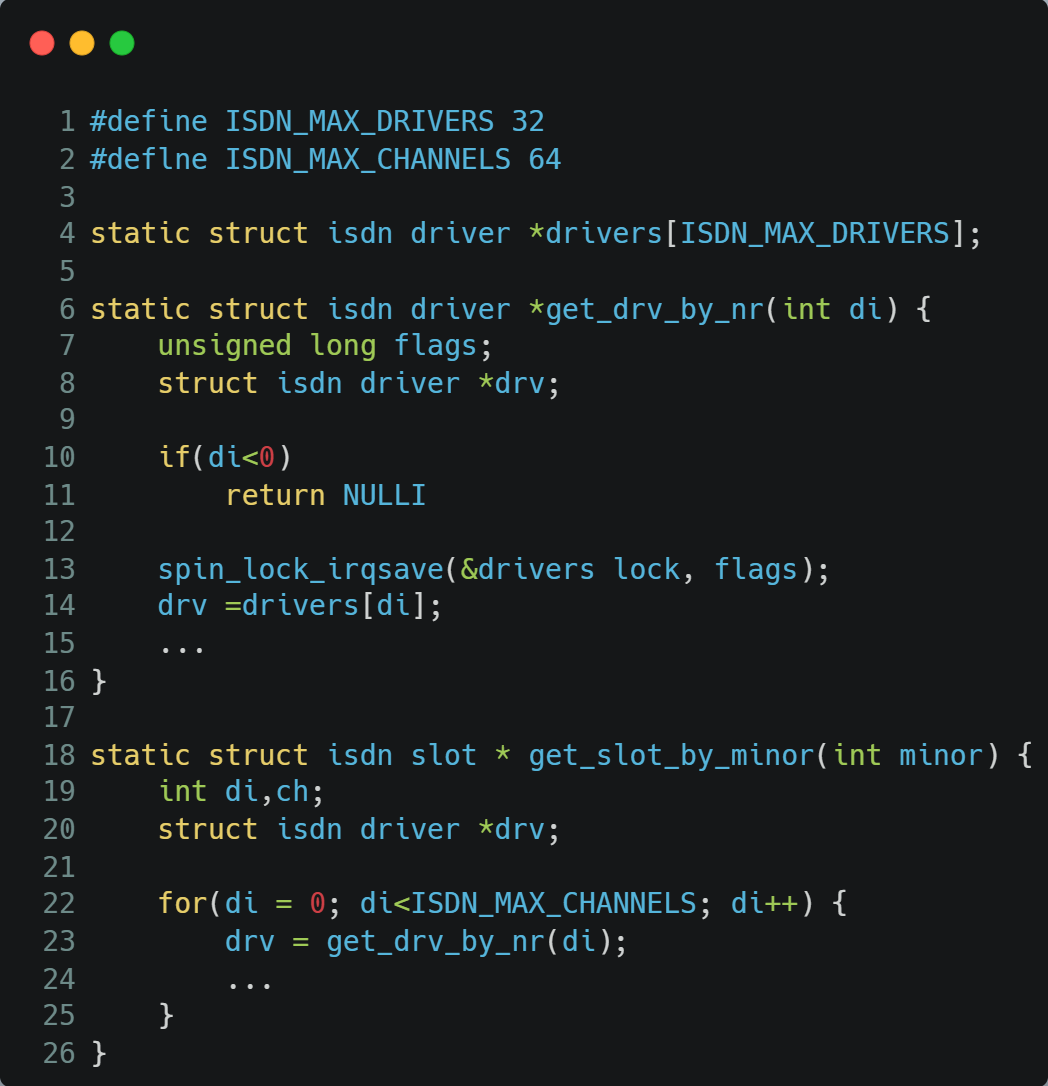
在执行分析之前,需要记录一些关键的信息。本例中主要是记录数组drivers的长度,将代码第4行数组drivers的长度记为32。
采用逆向的分析方法,从第14行开始分析,根据规则有变量di的约束0 <= di < 32。而di >= 32 || di < 0时,程序存在溢出漏洞。
第13行和di无关,不对其进行分析。
第10行,补充路径条件di >= 0,此时的漏洞触发的约束为(di >= 32 || di < 0) && di >= 0,将其简化为di >= 32时程序存在漏洞。
第8、7行和di无关,不对其进行分析。此时到达函数get_drv_by_nr的入口点,分析调用它的函数get_slot_by_minor,从第23行开始分析,此时函数get_slot_by_minor中di的漏洞触发约束为di >= 32时,程序存在漏洞。
通过分析第22行,得到约束0 <= di <= 64,利用约束求解器求解约束(0 <= di <= 64) && di >= 32,发现约束可满足,这时认为程序存在漏洞。
与其他漏洞分析技术结合
使用符号执行技术分析程序的一个好处是,可以分析程序路径的可行性,即该路径是否可达。通过对路径可行性进行分析,可以排除对那些不可能执行的程序路径的分析。这一方面在一定程度上缩小了分析范围,另一方面也使分析结果更精确。
在其他的静态漏洞分析过程中加入路径可行的分析,那么在漏洞分析过程中,与一些不可能被执行的路径的相关的结果将会在分析过程中被舍去,从而在一定程度上减少了误报。
通常,使用数据流分析或者污点分析技术的漏洞分析工具,都可以将符号执行融入实际分析过程中。
在通过数据流分析或污点传分析出程序的疑似漏洞之后,通过符号执行和约束求解,计算出可能触发漏洞的输入范围,如果该输入范围不为空集,则代码中可能存在漏洞,否则即为误报。
总结
上述例子中的符号约束只是单一符号变量的单一约束,实际中的情况要复杂得多。比如对带有多个符号变量的约束进行求解,或者对非线性的不等式进行求解。在这些复杂情况下约束求解器很可能不具备求解此类约束的能力,这时符号执行也就失去了其作用。
不过在很多时候,符合执行配合其它分析技术,可以大大提高分析的精度,有效减少漏报和误报率,成为漏洞分析的强力工具。
