平衡树的左旋

好的，树的左旋（Left Rotation）是平衡二叉树（如 ​AVL树​ 或 ​红黑树）中用于恢复平衡的一种基本操作。它通常是在右子树过高时进行，通过调整节点位置来降低高度。

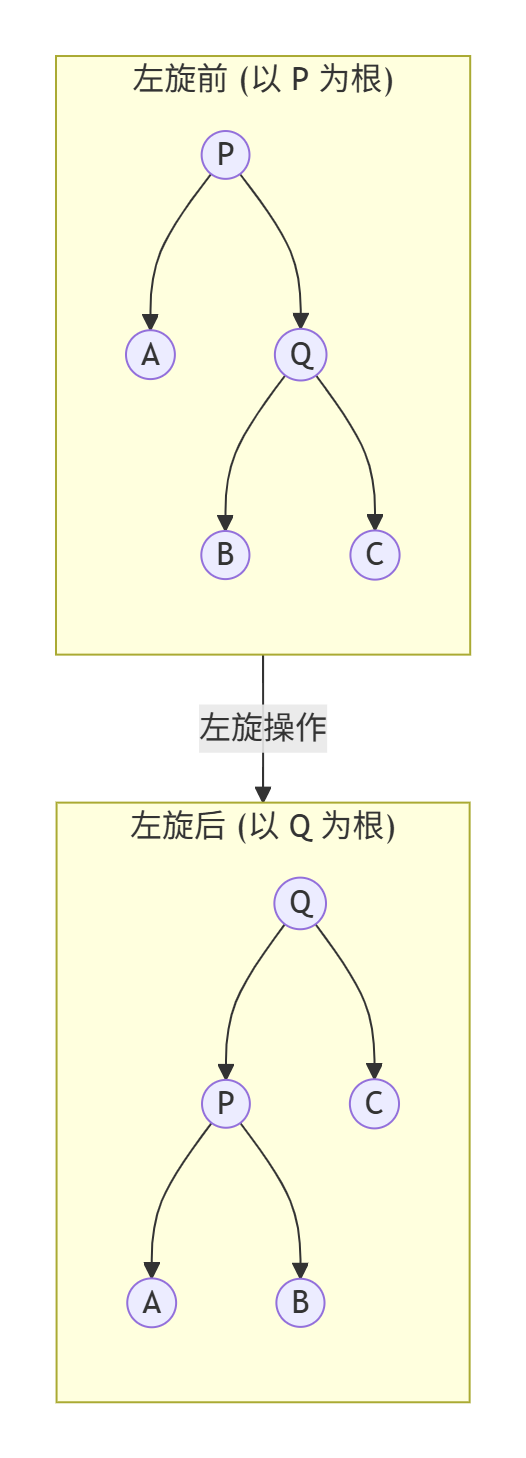
为了更直观地理解，我们来看一个左旋的示意图。下图展示了以节点 P为根进行左旋的过程：

---

​核心思想​

左旋操作围绕一个节点（如上图的 P）进行，将其“下放”到其右子节点（Q）的左侧，并让 Q成为新的根节点。这就像把树的局部结构向左“旋转”了一下。

​左旋步骤（围绕节点 P旋转）​​

假设我们对节点 P进行左旋，其右子节点为 Q：

1. ​接管左子树​：将 Q的左子树（B）作为 P的新右子树。

2. ​更新父指针​：如果 Q有左子树 B，则将其父指针指向 P。

3. ​链接新父子​：将 P的父节点（如果存在）指向 Q，建立新的父子关系。

4. ​确立新关系​：将 Q的左子节点设置为 P，完成旋转。

​伪代码（C++风格）​​

// 假设节点结构为：
struct Node {int key;Node *left;Node *right;// AVL树可能还包含：int height;// 红黑树可能还包含：string color;
};Node* leftRotate(Node *P) {// 1. 获取 P 的右子节点 QNode *Q = P->right;// 2. 将 Q 的左子树作为 P 的新右子树P->right = Q->left;// 3. 让 P 成为 Q 的新左子节点Q->left = P;// 4. 更新节点的高度（或平衡因子），这部分是平衡树特有的维护逻辑// updateHeight(P);// updateHeight(Q);// 5. 返回新的根节点 Q，调用者需要将其与树的其他部分连接return Q;
}

​时间复杂度​

⏳ O(1)。该操作只涉及修改有限数量的指针，是常数时间复杂度。

​何时使用左旋？​​

左旋是平衡二叉树算法的核心子例程。当检测到某个节点的右子树比左子树高​（即“不平衡”）时，就会根据具体情况使用左旋或先右旋再左旋（LR旋转）来恢复平衡。

操作	数据结构	目的
​链表左旋​	线性链表	循环移位
​树左旋​	平衡二叉树（AVL, 红黑树）	降低高度，恢复平衡

希望这个解释和示意图能帮助你清晰地理解树的左旋操作！