软考中级习题与解答——第一章_数据结构与算法基础(3)
例题21

1、知识点总结

2、选项分析
数组声明为 a[0..3, 0..2, 1..4],各维度长度:
- 第 1 维(最外层):3 - 0 + 1 = 4(索引 0、1、2、3)。
- 第 2 维:2 - 0 + 1 = 3(索引 0、1、2)。
- 第 3 维:4 - 1 + 1 = 4(索引 1、2、3、4)。
目标元素是 a[2, 2, 2],按行优先存储(最外层维度变化最慢,最内层维度变化最快),计算偏移量需统计 “在 a[2,2,2]之前的元素总数”:
第 1 维为 0 时: 第 2 维从 0 到 2,第 3 维从 1 到 4,元素总数为 3*4 = 12。
第 1 维为 1 时: 同理,元素总数为 3*4 = 12。
第 1 维为 2 时:
- 第 2 维为 0 时,第 3 维从 1 到 4,元素总数为1*4 = 4。
- 第 2 维为 1 时,第 3 维从 1 到 4,元素总数为1*4 = 4。
- 第 2 维为 2 时,第 3 维从 1 到 2(因为要找 a[2,2,2]之前的元素,第 3 维到 1 为止),元素总数为1*2=2
将以上三部分相加,总元素数为: 12 + 12 + 4 + 4 + 2 = 34
由于每个元素占 1 个存储单元,所以 a[2,2,2]相对base_a 的偏移量是 34-1=33
3、最终答案:C
例题22

1、知识点总结
二叉树节点度数的基本关系
在任何非空二叉树中,我们都可以根据节点的度(即孩子节点的数量)来对节点进行分类:

完全二叉树的特殊性质

在完全二叉树中,除了最后一个非叶子节点外,所有非叶子节点都必须有两个孩子(度为2)。只有最后一个非叶子节点,在总节点数为偶数时,才可能只有一个左孩子(度为1)。如果总节点数为奇数,那么所有节点要么是叶子,要么就有两个孩子,不存在度为1的节点。
2、选项分析


3、最终答案:B
例题23

1、知识点总结
循环队列
循环队列是将顺序队列(普通数组)在逻辑上“首尾相连”,形成一个环状结构。这样做是为了解决普通队列在出队操作后,数组前端会产生“假溢出”(数组里有空间,但队尾指针已到末尾无法入队)的问题。
核心元素
数组: 物理存储空间。
队首指针 (front): 指向队首元素的位置(或队首元素的前一个位置)。
队尾指针 (rear): 指向队尾元素的位置(或队尾元素下一个可插入的位置)。
模运算 (mod m): 实现循环的关键,确保指针在到达数组末尾后能“绕回”到数组开头。
2、选项分析
rear 指向队尾元素,且队列中有4个元素,我们可以从队尾向前倒数4个位置来找到队首。
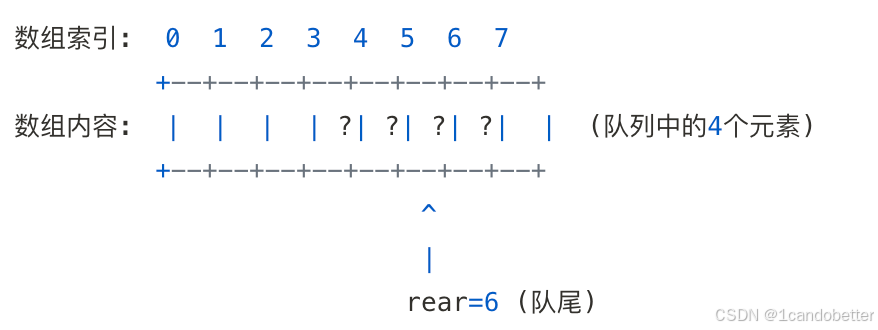
队尾元素 在索引 6。
队尾前一个元素 在索引 5。
队尾前二个元素 在索引 4。
队尾前三个元素 (即队首元素) 在索引 3。
所以,front = 3。front = 6 - 4 + 1 = 3。但是,我们需要考虑“循环”的情况,公式如下:
front = (rear - length + 1 + m) mod m
3、最终答案:C
例题24

1、知识点总结
哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,也称为最优二叉树。哈夫曼树的特点是:
- 哈夫曼树中没有度为 1 的节点(即每个非叶子节点都有两个子节点)。


2、选项分析
 3、最终答案:C
3、最终答案:C
例题25

1、知识点总结
广义表的长度:广义表中最外层元素的个数(不考虑嵌套,只看最外层有几个逗号分隔的元素)。
广义表的深度:广义表中括号的最大嵌套层数(从最外层开始数,每嵌套一层深度加 1)。
2、选项分析


3、最终答案:B
例题26

1、知识点总结
二叉树的遍历有三种主要方式:
- 先序遍历:先访问根节点,再先序遍历左子树,最后先序遍历右子树(根 - 左 - 右)。
- 中序遍历:先中序遍历左子树,再访问根节点,最后中序遍历右子树(左 - 根 - 右)。
- 后序遍历:先后序遍历左子树,再后序遍历右子树,最后访问根节点(左 - 右 - 根)。
已知先序和中序遍历序列,可以唯一确定一棵二叉树,进而得到后序遍历序列。
2、选项分析
步骤 1:确定根节点
先序遍历序列为 ABDECF,先序遍历的第一个节点是根节点,所以根节点为 A。
步骤 2:划分左、右子树(根据中序遍历)
中序遍历序列为 DBEAFC,根节点 A 将中序序列分为左子树部分 DBE 和右子树部分 FC。
步骤 3:构建左子树
先序遍历左子树部分的序列是 BDE(先序序列中根节点 A 之后的部分,对应左子树的先序遍历)。
中序遍历左子树部分的序列是 DBE。
同理,先序遍历左子树的第一个节点 B 是左子树的根节点,中序序列中 B 左边是 D,右边是 E,所以左子树的结构为:B 是根,左孩子是 D,右孩子是 E。
步骤 4:构建右子树
先序遍历右子树部分的序列是 CF(先序序列中对应右子树的部分)。
中序遍历右子树部分的序列是 FC。
先序遍历右子树的第一个节点 C 是右子树的根节点,中序序列中 C 左边是 F,所以右子树的结构为:C 是根,左孩子是 F,无右孩子。
步骤 5:确定后序遍历序列
后序遍历是左 - 右 - 根。左子树的后序遍历序列是 DEB,右子树的后序遍历序列是 FC,根节点是 A,所以整体后序遍历序列是 DEBFCA。
3、最终答案:D
例题27

1、知识点总结

2、选项分析



3、最终答案:C
例题28
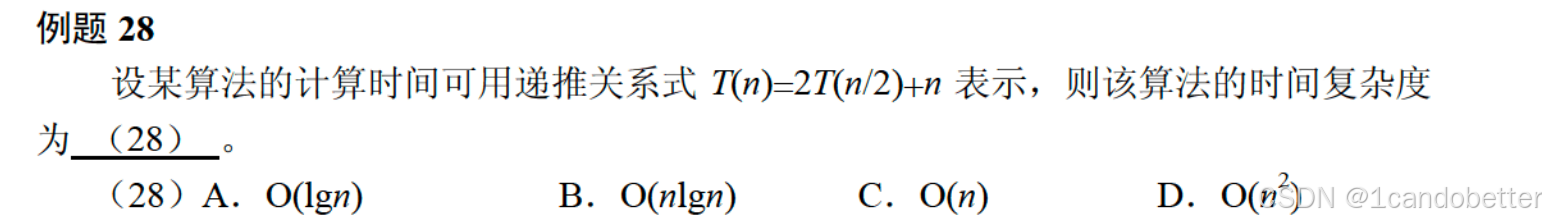
1、知识点总结


2、选项分析

3、最终答案:B
例题29

1、知识点总结
- 分治算法:将大问题分解为规模较小、结构相似的子问题,子问题解法与原问题一致,通常天然适合用递归实现(如归并排序、快速排序的分治过程)。
- 动态规划:通过分解问题为重叠子问题,利用子问题的解构建原问题的解,很多场景下会通过递归式(如斐波那契数列的递归推导)来分析,再优化为非递归的动态规划,与递归联系较深。
- 贪心算法:每一步都做出局部最优选择,以期望得到全局最优,通常是迭代式地进行选择(如找零钱问题,每次选面值最大的硬币),不需要依赖递归调用子问题,与递归关联最弱。
- 回溯算法:通过递归尝试所有可能的解,当当前路径不符合要求时回退,递归是其核心实现方式(如八皇后问题的递归回溯)。
2、选项分析
- 选项 A(分治):分治的 “分解 - 解决子问题 - 合并” 流程与递归高度契合,联系紧密。
- 选项 B(动态规划):虽可优化为非递归,但递归是分析子问题依赖的重要手段,联系较深。
- 选项 C(贪心):贪心的局部最优选择是迭代执行的,无需递归调用,与递归联系最弱。
- 选项 D(回溯):回溯的 “尝试 - 回退” 逻辑完全依赖递归实现,联系非常紧密。
3、最终答案:C
例题30

1、知识点总结
涉及以下排序算法的特点:
- 直接插入排序:逐个将元素插入已排序序列,若仅需前 k 个有序,仍需对整个序列逐步插入,无针对性优化。
- 希尔排序:基于插入排序的改进,按增量分组排序,是全局排序算法,不适合仅需前 k 个有序的场景。
- 快速排序:分区后递归排序左右子序列,是全局排序算法,若要得到前 k 个有序,需完成大部分排序过程,效率不高。
- 堆排序:利用大根堆(或小根堆)的性质,每次可快速得到当前最大(或最小)元素。若需前 k 个元素有序,只需构建堆后,执行 k 次 “取堆顶 + 调整堆” 操作,无需对整个序列完全排序,效率很高。
