当前位置：首页 > news >正文

【机器学习入门】3.1 关联分析——从“购物篮”到推荐系统的核心逻辑

news 2025/8/30 9:02:05

你有没有想过：为什么淘宝会推荐 “买了牛奶的人还会买面包”？为什么超市会把啤酒和尿不湿放在一起？这些 “精准关联” 的背后，靠的就是机器学习中的关联分析技术。

这篇文章会从 “生活化例子” 切入，帮你吃透关联分析的核心概念（关联规则、支持度、置信度），再详解两大核心算法（ALS、FP）的原理与应用，所有内容贴合入门学生的认知，不堆砌复杂公式，只讲 “能懂、能用” 的干货，让你明白 “关联分析如何从数据中挖规律，又如何落地到推荐场景”。

一、关联分析基础：从 “购物篮” 理解核心概念

关联分析（又称关联挖掘）是机器学习中 “挖掘数据内在联系” 的经典技术，最典型的场景就是购物篮分析—— 通过分析用户的购物记录，找出 “哪些商品经常被一起购买”，进而指导运营（如商品摆放、推荐）。我们先从三个核心概念入手：关联分析、关联规则、频繁项集。

1.1 关联分析：找 “数据中的隐藏关联”

定义

关联分析是在交易数据、关系数据等信息载体中，查找项目集合或对象集合之间的频繁模式、关联、相关性的技术。简单说，就是从数据中挖 “哪些东西总是一起出现”。

经典例子：购物篮分析

假设超市有以下 5 条用户购物记录（事务数据），每条记录（TID）代表一次购物的商品集合：

TID（事务 ID）	购买商品集合（项集）
1	面包、牛奶、鸡蛋
2	面包、尿布、啤酒
3	牛奶、尿布、啤酒、可乐
4	面包、牛奶、尿布、啤酒
5	面包、牛奶、尿布、可乐

通过关联分析，我们能发现这样的规律：

“面包 + 牛奶” 经常一起被购买；
“尿布 + 啤酒” 的组合出现频率很高（这就是沃尔玛经典的 “啤酒与尿不湿” 案例的简化版）。

这些规律就是关联分析要挖掘的 “频繁模式”，也是后续生成 “推荐规则” 的基础。

1.2 关联规则：“如果买 X，就可能买 Y” 的逻辑

找到频繁模式后，我们需要把它转化为 “可落地的规则”—— 这就是关联规则。

定义

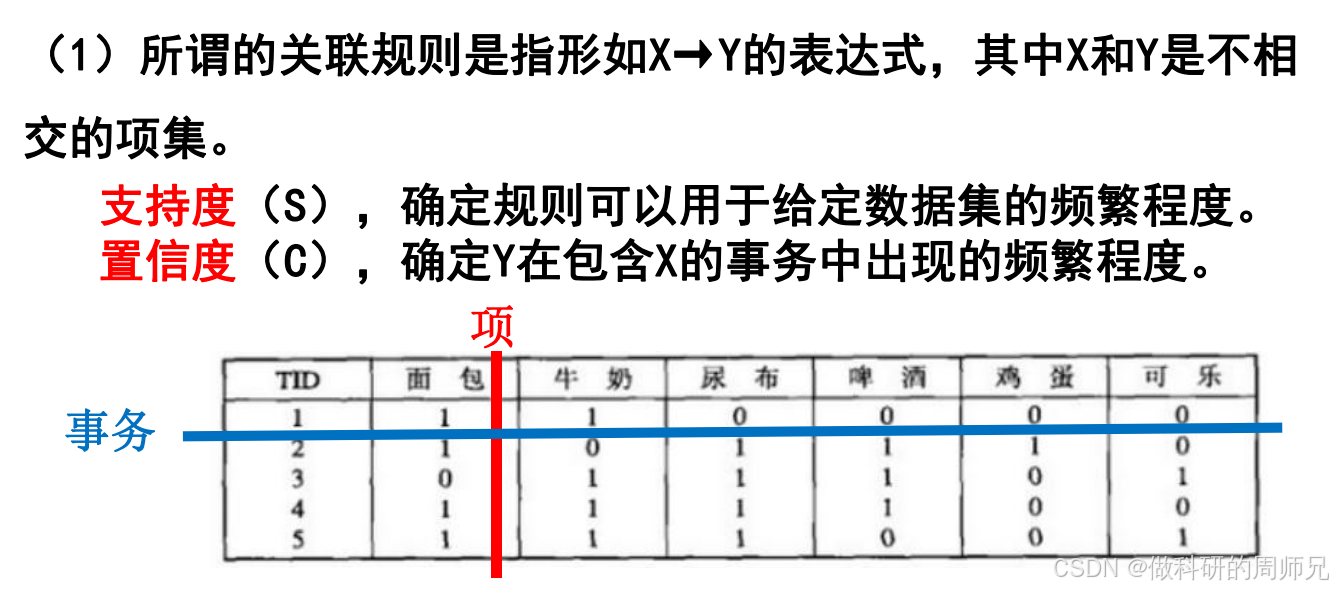
关联规则是形如 X→Y 的表达式，其中：

X 是 “前件”（规则头）：表示 “用户购买了 X”；
Y 是 “后件”（规则体）：表示 “用户可能购买 Y”；
X 和 Y 是不相交的项集（不能有重叠商品，比如 “面包→面包” 没有意义）。

例子

从上面的购物数据中，我们可以提取出这些关联规则：

面包→牛奶（如果用户买了面包，可能还会买牛奶）；
尿布→啤酒（如果用户买了尿布，可能还会买啤酒）；
面包 + 牛奶→尿布（如果用户买了面包和牛奶，可能还会买尿布）。

1.3 衡量关联规则的两大指标：支持度与置信度

不是所有关联规则都有价值 —— 比如 “买可乐→买钢琴” 这种规则几乎不会出现，没有实际意义。我们需要用支持度（S） 和置信度（C） 两个指标，筛选出 “频繁且可信” 的规则。

1. 支持度（S）：规则的 “频繁程度”

支持度衡量 “X 和 Y 一起出现的频率”，反映规则在数据集中的普遍程度。如果支持度太低，说明规则只在极少数情况下出现，没有推广价值。

计算公式

例子计算（用上面的 5 条事务数据）

计算规则 “尿布→啤酒” 的支持度：

同时包含 “尿布” 和 “啤酒” 的事务：TID2、TID3、TID4（共 3 条）；
总事务数：5；
支持度 S(尿布→啤酒) = 3/5 = 0.6（即 60%）。

2. 置信度（C）：规则的 “可信程度”

置信度衡量 “在买了 X 的前提下，买 Y 的概率”，反映规则的可靠性 —— 置信度越高，说明 “买 X 后买 Y” 的可能性越大。

计算公式

例子计算

还是计算规则 “尿布→啤酒” 的置信度：

同时包含 “尿布” 和 “啤酒” 的事务：3 条（TID2、TID3、TID4）；
包含 “尿布” 的事务：TID2、TID3、TID4、TID5（共 4 条）；
置信度 C(尿布→啤酒) = 3/4 = 0.75（即 75%）。

关键结论：筛选 “强规则”

只有同时满足 “最小支持度阈值” 和 “最小置信度阈值” 的关联规则，才被称为强规则（有实际应用价值）。比如设定最小支持度 = 0.4、最小置信度 = 0.6：

“尿布→啤酒” 的支持度 0.6（≥0.4）、置信度 0.75（≥0.6），是强规则；
若有规则 “可乐→面包”，支持度 = 1/5=0.2（<0.4），则不是强规则。

1.4 关联分析的核心策略：两步生成强规则

关联分析的过程分两步，逻辑清晰，所有关联算法（包括后面的 FP 算法）都遵循这个框架：

第一步：生成 “频繁项集”

目标：找出所有 “满足最小支持度阈值” 的商品集合（项集），这些项集就是频繁项集；
为什么要先找频繁项集？因为 “非频繁的项集” 不可能生成 “强规则”（支持度不够），先过滤掉非频繁项集，能大幅减少后续计算量；
例子：在上面的购物数据中，若最小支持度 = 0.4（即至少出现 2 次），则 “尿布 + 啤酒”（出现 3 次）、“面包 + 牛奶”（出现 4 次）是频繁项集；“鸡蛋”（只出现 1 次）不是频繁项集。

第二步：从频繁项集中生成 “强规则”

目标：对每个频繁项集，生成所有可能的关联规则，再筛选出 “满足最小置信度阈值” 的强规则；
例子：从频繁项集 “面包 + 牛奶 + 尿布” 中，可生成规则 “面包 + 牛奶→尿布”“面包 + 尿布→牛奶” 等，再计算每个规则的置信度，保留达标的强规则。

二、关联与推荐：关联分析如何落地到推荐系统？

关联分析的核心应用之一就是推荐系统—— 通过挖掘用户行为的关联规律，推测用户可能喜欢的商品 / 内容。我们结合两种经典推荐方式（基于内容、基于协同），看关联分析如何发挥作用。

2.1 基于内容的推荐：用关联规则做 “直接推荐”

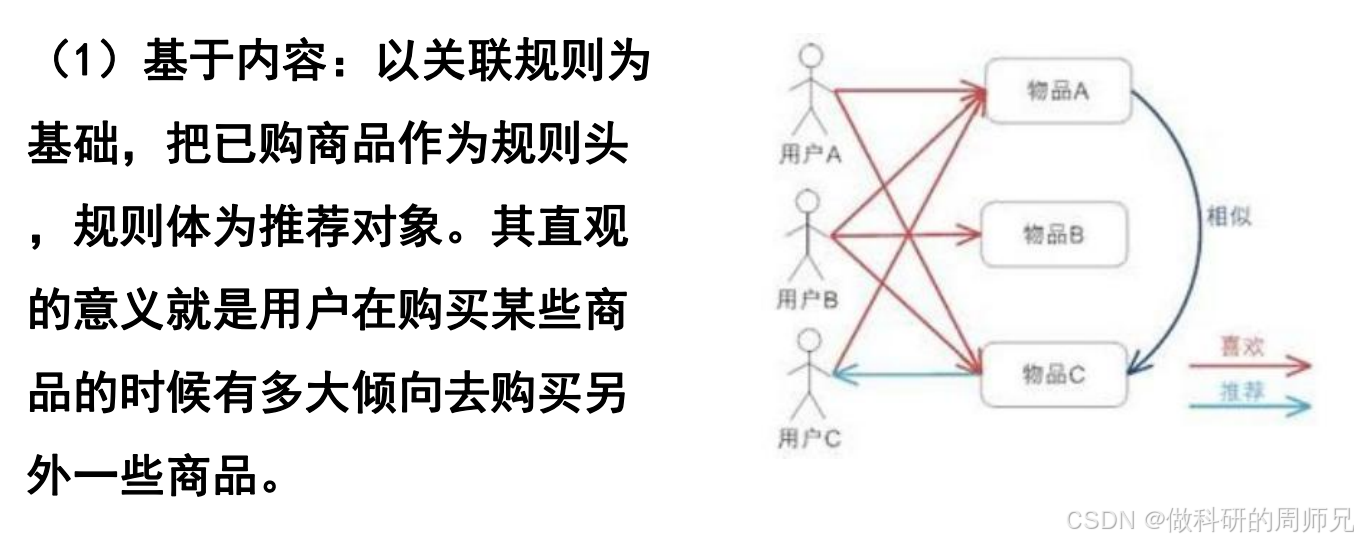
核心逻辑

以 “用户已购商品” 为关联规则的 “前件 X”，以 “频繁一起购买的商品” 为 “后件 Y”，直接推荐 Y 给用户。本质是 “利用关联规则的置信度，判断用户购买 Y 的倾向”。

例子

假设通过关联分析得到强规则：

面包→牛奶（置信度 0.8）；
尿布→啤酒（置信度 0.75）；
牛奶 + 面包→鸡蛋（置信度 0.6）。

当用户购物时：

若用户加入 “面包” 到购物车，系统会推荐 “牛奶”（因为规则 “面包→牛奶” 置信度高）；
若用户同时加入 “牛奶” 和 “面包”，系统会额外推荐 “鸡蛋”。

适用场景

电商平台的 “购物车推荐”“买了还买” 模块；
超市的商品摆放（比如把面包和牛奶放在相邻货架）。

2.2 基于协同的推荐：用关联思想做 “评分预测”

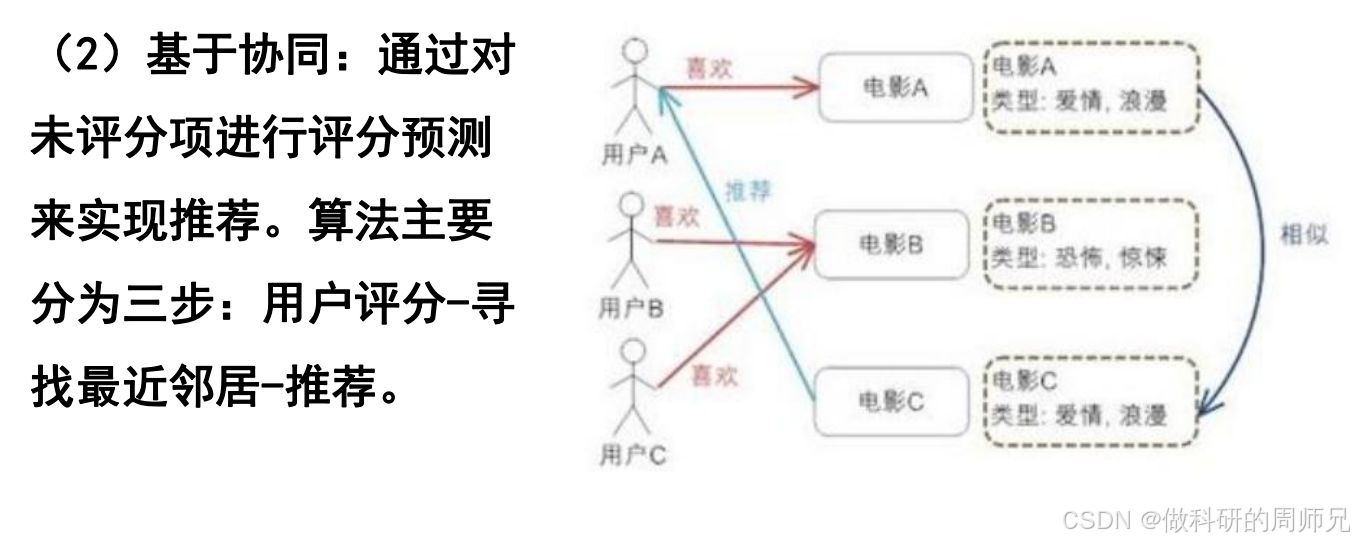
基于协同的推荐（协同过滤）虽然不直接用 “关联规则”，但核心思想和关联分析一致 ——“找相似用户 / 相似物品的关联”，通过 “评分预测” 实现推荐。协同过滤的三步流程，我们结合例子讲透：

三步流程（以电影推荐为例）

用户评分：构建 “用户 - 物品评分矩阵” 首先收集用户对物品的评分（比如 1-5 分，1 分最差，5 分最好），形成一个矩阵。假设我们有 3 个用户对 3 部电影的评分（“-” 表示未评分，需要预测）：
用户 \ 电影电影 A（爱情）电影 B（恐怖）电影 C（爱情）
用户 A 5 - 4
用户 B - 3 -
用户 C 4 2 5
寻找最近邻居：找 “兴趣相似的用户 / 物品”
- 相似用户：比如用户 A 和用户 C 都喜欢 “爱情电影”（对电影 A、C 评分高，对恐怖电影 B 评分低），所以 A 和 C 是 “最近邻居”；
- 相似物品：比如电影 A 和电影 C 都是 “爱情类型”，且用户对它们的评分趋势一致（A 给 A 打 5 分、C 打 4 分；A 给 C 打 4 分、C 打 5 分），所以 A 和 C 是 “相似物品”。
推荐：预测未评分项，推荐高分物品
- 比如预测用户 A 对 “电影 B” 的评分：用户 A 的最近邻居是 C，C 给 B 打 2 分，所以预测 A 对 B 的评分约为 2 分（不推荐）；
- 比如预测用户 B 对 “电影 A” 的评分：电影 A 的相似物品是 C，但 B 没给 C 评分，可找 “喜欢恐怖电影 B 的用户”（比如无直接相似用户，可扩大范围），若预测评分低，则不推荐；若预测用户 B 对 “电影 C” 评分高，则推荐电影 C。

用户 \ 电影	电影 A（爱情）	电影 B（恐怖）	电影 C（爱情）
用户 A	5	-	4
用户 B	-	3	-
用户 C	4	2	5

关联思想的体现

协同过滤的核心是 “利用相似性关联”—— 要么关联 “相似用户的行为”（用户协同），要么关联 “相似物品的评分”（物品协同），这和关联分析 “找数据中的关联规律” 的本质是一致的。

三、ALS 算法：协同过滤的 “高效实现方案”

在协同过滤中，“用户 - 物品评分矩阵” 通常是稀疏的（比如 1000 个用户对 1000 部电影，可能只有 1% 的评分数据），直接计算相似性会很耗时。ALS（交替最小二乘法）算法通过 “矩阵分解” 解决了稀疏性问题，是工业界常用的协同过滤算法。

3.1 ALS 的核心思想：用 “低维特征” 表示用户与物品

ALS 的核心是把 “稀疏的用户 - 物品评分矩阵” 分解为两个 “稠密的低维矩阵”，通过这两个矩阵的乘积，近似还原原评分矩阵（包括未评分的项）。

矩阵分解的逻辑

例子（简化版）

假设 k=2（两个特征：爱情偏好度、恐怖偏好度）：

3.2 ALS 的 “交替优化” 过程

ALS 的名字 “交替最小二乘法” 来源于它的优化逻辑 —— 交替优化用户特征矩阵 U 和物品特征矩阵 V，直到误差最小：

固定 V，优化 U 假设物品特征矩阵 V 已知，我们通过 “最小化预测评分与真实评分的平方误差”，求解每个用户的特征向量（U 的每行）；
固定 U，优化 V 假设用户特征矩阵 U 已知，再通过同样的 “最小化平方误差”，求解每个物品的特征向量（V 的每列）；
重复交替 不断重复 “固定 V 优化 U→固定 U 优化 V” 的过程，直到误差收敛（不再明显下降），此时得到的 U 和 V 就是最优的低维特征矩阵。

3.3 ALS 的应用场景

ALS 算法因为 “能高效处理稀疏矩阵”，广泛应用于需要 “评分预测” 的推荐场景：

视频平台：如 Netflix 用 ALS 预测用户对电影的评分，推荐高分电影；
电商平台：如亚马逊用 ALS 预测用户对商品的 “潜在评分”，推荐 “你可能喜欢” 的商品；
音乐平台：如 Spotify 用 ALS 预测用户对歌曲的偏好度，推荐个性化歌单。

四、FP 算法：高效挖掘频繁项集的 “利器”

在关联分析的 “第一步生成频繁项集” 中，早期的 Apriori 算法需要 “多次扫描数据”（比如每次生成候选项集都要扫一遍事务数据），当数据量很大时（比如百万级购物记录），效率很低。FP 算法（FP-Tree 算法）通过 “构建 FP 树” 实现 “一次扫描数据”，大幅提升了频繁项集的挖掘效率。

4.1 FP 算法的核心优势：解决 Apriori 的 “效率痛点”

Apriori 算法的问题：比如要挖掘 “3 项频繁集”，需要先扫描数据找 “1 项频繁集”，再扫描找 “2 项频繁集”，再扫描找 “3 项频繁集”—— 数据量越大，扫描次数越多，耗时越长。

FP 算法的改进：

只扫描数据两次：第一次统计 “每个项的出现频率”，第二次构建 FP 树；
用 FP 树 “压缩存储” 事务数据：把所有事务的频繁项按 “频率降序” 存储在树上，避免重复存储，减少计算量。

4.2 FP 算法的两步流程（以购物篮数据为例）

FP 算法的核心是 “先建 FP 树，再从树中挖掘频繁项集”，我们结合之前的 5 条购物数据（TID1-TID5），一步步拆解：

第一步：预处理数据，构建 “项头表”

统计项频：计算每个商品的出现次数（项频），并按 “项频降序” 排序（过滤掉非频繁项，假设最小支持度 = 2，项频≥2）：
- 面包：4 次（TID1、2、4、5）；
- 牛奶：4 次（TID1、3、4、5）；
- 尿布：4 次（TID2、3、4、5）；
- 啤酒：3 次（TID2、3、4）；
- 可乐：2 次（TID3、5）；
- 鸡蛋：1 次（TID1，非频繁，过滤）。
构建项头表：记录每个频繁项的 “项频” 和 “在 FP 树中的位置指针”（用于后续挖掘）：

频繁项	项频	FP 树指针
面包	4	指向树中所有 “面包” 节点
牛奶	4	指向树中所有 “牛奶” 节点
尿布	4	指向树中所有 “尿布” 节点
啤酒	3	指向树中所有 “啤酒” 节点
可乐	2	指向树中所有 “可乐” 节点

事务排序：将每条事务中的 “非频繁项删除”，剩余频繁项按 “项频降序” 排序：
- TID1（面包、牛奶、鸡蛋）→ 删鸡蛋 → [面包、牛奶]；
- TID2（面包、尿布、啤酒）→ [面包、尿布、啤酒]；
- TID3（牛奶、尿布、啤酒、可乐）→ [牛奶、尿布、啤酒、可乐]（牛奶和尿布项频都是 4，顺序可互换）；
- TID4（面包、牛奶、尿布、啤酒）→ [面包、牛奶、尿布、啤酒]；
- TID5（面包、牛奶、尿布、可乐）→ [面包、牛奶、尿布、可乐]。

第二步：构建 FP 树，挖掘频繁项集

构建 FP 树： FP 树是一棵 “前缀树”，每个节点代表一个频繁项，父节点代表 “前缀项”，节点的 “计数” 代表 “该前缀路径出现的次数”。构建过程是 “逐条插入排序后的事务”：
- 插入第一条事务 [面包、牛奶]：树的根节点→面包（计数 1）→牛奶（计数 1）；
- 插入第二条事务 [面包、尿布、啤酒]：根节点→面包（计数 2）→尿布（计数 1）→啤酒（计数 1）；
- 后续事务依次插入，重复的前缀路径会累加计数（比如第三条事务 [牛奶、尿布、啤酒、可乐]，根节点→牛奶（计数 1）→尿布（计数 1）→啤酒（计数 1）→可乐（计数 1））；
- 最终的 FP 树会压缩所有事务的频繁项信息，每个节点的计数反映 “该项在特定前缀下的出现次数”。
挖掘频繁项集：从 “项头表的最后一项（项频最低的项）” 开始，通过 “项头表的指针找到该项目在 FP 树中的所有节点”，再构建 “条件 FP 树”，递归挖掘频繁项集：
- 比如从 “可乐” 开始：找到可乐在树中的节点（计数 2），其前缀路径是 [牛奶、尿布]（计数 1）和 [面包、牛奶、尿布]（计数 1），构建 “可乐的条件 FP 树”，再从条件树中挖掘包含 “可乐” 的频繁项集（如 [尿布、可乐]、[牛奶、尿布、可乐]）；
- 按项头表逆序（可乐→啤酒→尿布→牛奶→面包）依次挖掘，最终得到所有满足最小支持度的频繁项集。