当前位置： 首页 > news >正文

CD71.【C++ Dev】二叉树的三种非递归遍历方式

news 2025/8/30 7:03:21

目录

1.知识回顾

2.前序遍历

分析

总结入栈的几种可能

循环的条件

代码

提交结果

3.中序遍历

分析

代码

提交结果

3.★后序遍历

分析

问题:如何确定是第一次访问到栈的元素还是第二次访问到栈中的元素?

方法1:使用填充的内存(依赖于架构)

判断计算机使用的架构和指针大小

代码

提交结果

方法2:寻找规律,设置一个prev变量记录上一个访问的节点

代码

运行结果

方法3:使用标记栈

代码

运行结果

1.知识回顾

106.【C语言】数据结构之二叉树的三种递归遍历方式

L17.【LeetCode题解】前序遍历

L18.【LeetCode题解】中序遍历和后序遍历

2.前序遍历

https://leetcode.cn/problems/binary-tree-preorder-traversal/

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]

输出：[1,2,3]

解释：

示例 2：

输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

分析

以这棵树[8,3,10,1,6,null,null,null,null,4,7]为例分析:

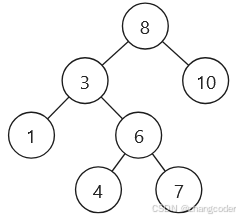
前序遍历必然最先访问左路节点,其次是左路节点的右子树,需要一直重复这个过程

那么可以分成两部分:

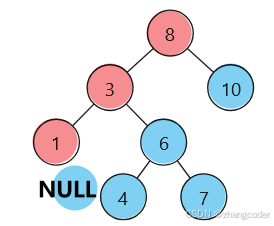
(红色是左路节点,蓝色是左路节点的右子树)

访问顺序:8→3→1→1的右子树→3的右子树→8的右子树

会发现:记录8→3→1遍历顺序 又要访问1、3、8的右子树(恰好是8、3、1倒过来的顺序)

可以利用栈:先访问左路节点(左路节点入前序遍历数组),后左路节点入栈(入栈的是节点的指针),访问左路节点的右子树需要使用栈顶元素,弹出的节点记录到前序遍历的数组中,而且需要使用一个指针cur从根节点开始遍历树

1. cur指向一个节点意味着访问一棵树的开始
2. 栈里面的节点意味着要访问它的右子树

树分成左路节点和右子树 右子树再分成左路节点和右子树 右子树再再分成左路节点和右子树……

先入左节点:

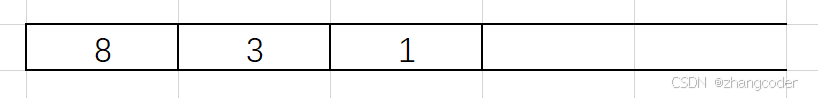
1的左子树为空,需要弹出栈顶元素,访问右节点

访问右子树前要先弹出左子树的所有节点:

1的左和右子树为NULL,直接弹出:

3的右子树不为NULL,弹出3后入右子树:

6的左子树为4,继续入栈:

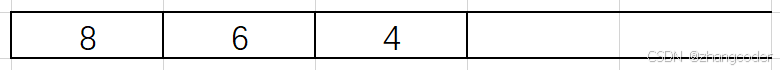
4的左和右子树节点为NULL,直接弹出:

6的右子树不为NULL,弹出6后入右子树:

7的左和右子树节点为NULL,直接弹出:

8的右子树不为NULL,弹出8后入右子树:

10的左和右子树节点为NULL,直接弹出:

栈为空,循环结束

总结入栈的几种可能

1.栈顶的左右子树都为空,直接弹出

2.栈顶的左子树不为空,将左子树入栈

3.栈顶的右子树不为空,弹出栈顶后,将右子树入栈

//必然最先访问左路节点
while(cur)
{st.push(cur);cur=cur->left;
}//左路节点的右子树,需要取栈顶元素
auto elem=st.top();
st.pop();
ret.push_back(elem->val);
cur=elem->right;//子问题的方式访问右子树

循环的条件

显然栈不为空就继续循环,但如果只写这个条件会导致有些测试用例过不了

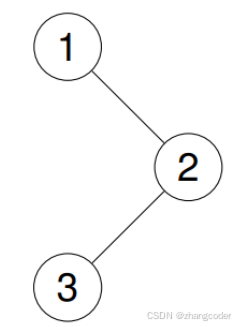
原因是1的左子树为空,将1出栈后,恰满足栈为空的循环退出条件,导致2和3没有访问到,需要添加cur如果不为空,也可以继续循环

而且"cur不为空"这个条件应该比"栈不为空"这个条件先判断,可以使用短路运算的规则:

while (cur || ! !st.empty())
{//......
}

代码

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {if (root==nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur=root;while (cur || !st.empty()){//必然最先访问左路节点while(cur){st.push(cur);ret.push_back(cur->val);cur=cur->left;}//访问左路节点的右子树,需要取栈顶元素auto elem=st.top();st.pop();cur=elem->right;// 子问题的方式访问右子树} return ret;}
};

提交结果

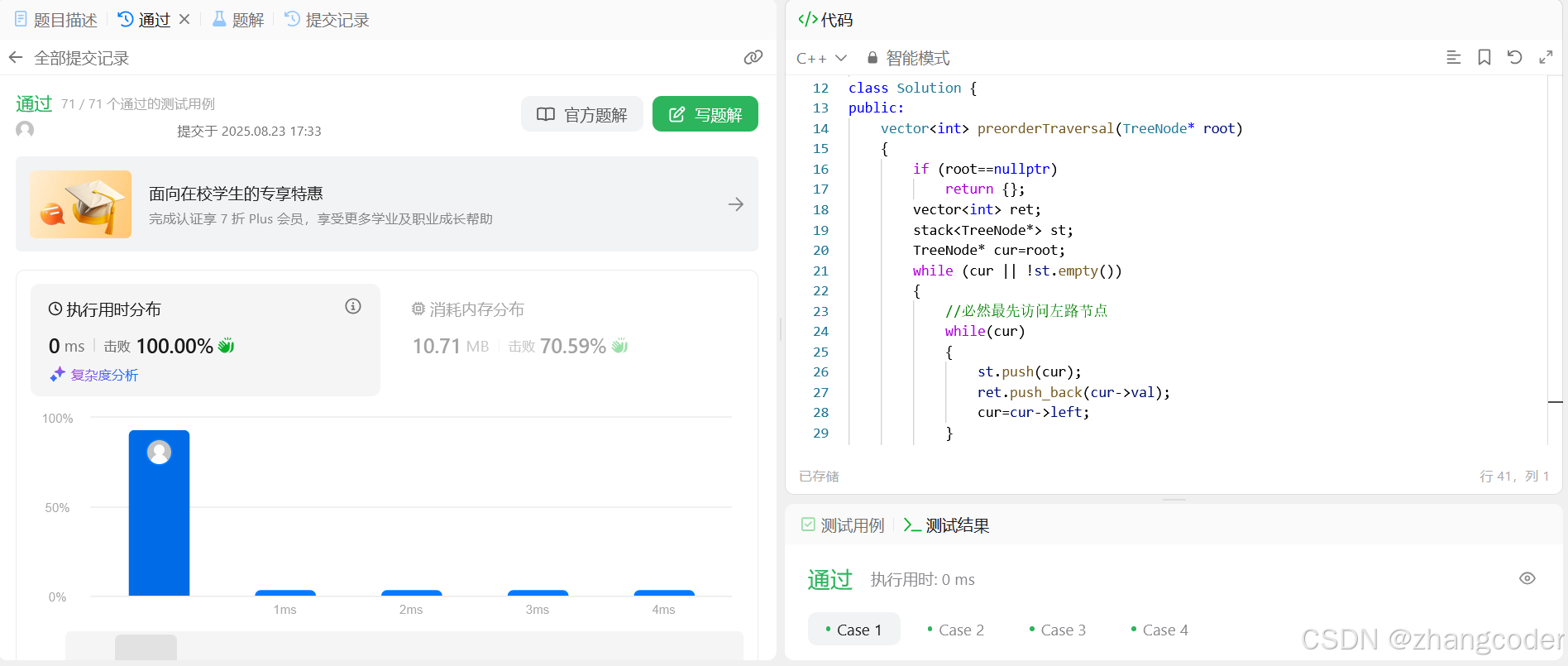
3.中序遍历

https://leetcode.cn/problems/binary-tree-inorder-traversal/

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

分析

中序遍历:左→根→右,即左子树访问完了才能访问根和右子树

反复执行这两步:

1. 左路节点入栈
2. 访问左路节点及左路节点的右子树

        从栈里面取到一个节点(pop)就意味这个节点左子树已经访问完了

稍微改改前序遍历的代码即可

代码

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {if (root==nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur=root;while (cur || !st.empty()){//先遍历左子树,但不访问其中的节点,即不要push_back到ret中while(cur){st.push(cur);cur=cur->left;}//左子树遍历完了,那就访问根和右子树auto elem=st.top();st.pop();ret.push_back(elem->val);cur=elem->right;// 子问题的方式访问右子树} return ret;}
};

提交结果

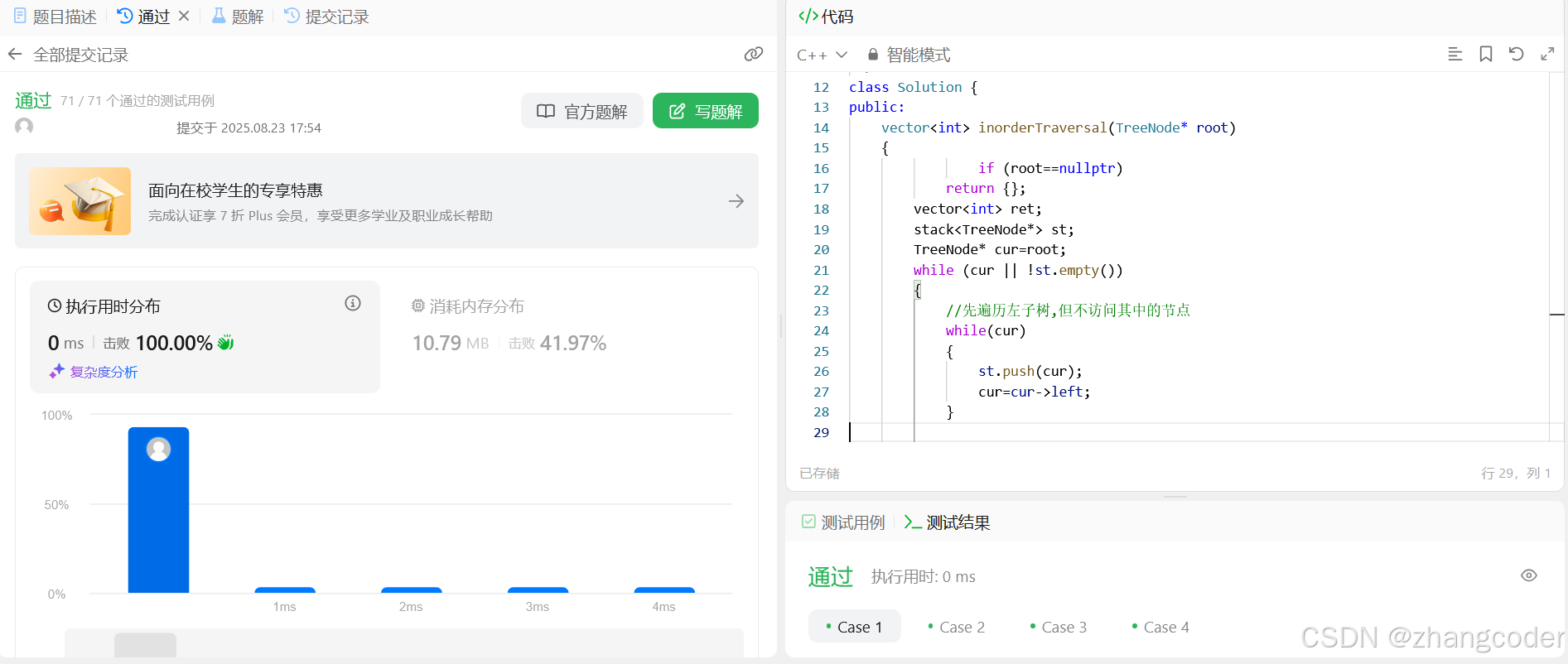
3.★后序遍历

https://leetcode.cn/problems/binary-tree-postorder-traversal/

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

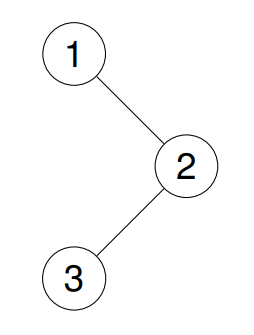
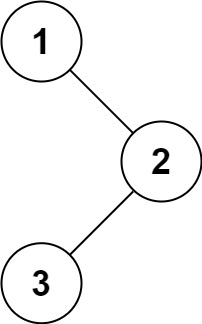
输入：root = [1,null,2,3]

输出：[3,2,1]

解释：

示例 2：

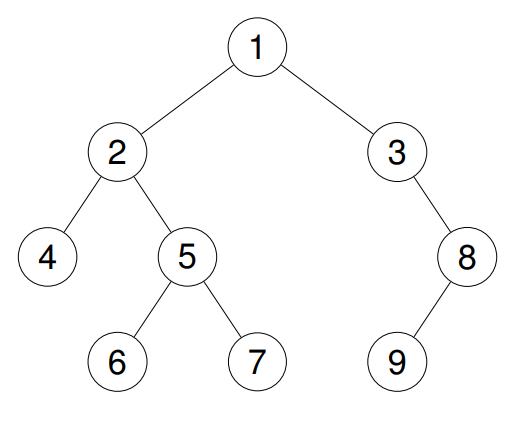
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[4,6,7,5,2,9,8,3,1]

解释：

示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

提示：

  • 树中节点的数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

分析

后序遍历:左→右→根,即必须访问完左子树和右子树才能访问根

以这棵树[8,3,10,1,6]为例分析:

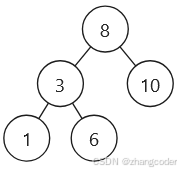
仍然分成两部分:

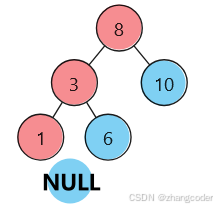
(红色是左路节点,蓝色是左路节点的右子树)

左路节点入栈:

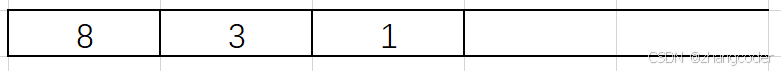
1的左和右子树为NULL,直接弹出1,将1记录到后序遍历的数组中:

虽然3的右子树不为空,但是不能弹出3,如果弹出3那就成前序遍历了,应该等第二次访问到栈里面的3才弹出3(即将3的左右子树都访问完才能访问根节点3)

入3的右子树

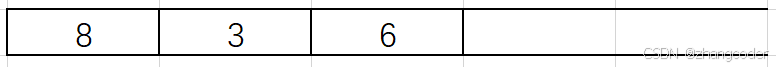
6的左和右子树为NULL,直接弹出6,将6记录到后序遍历的数组中:

第二次遇到3,因为3的左右子树都访问完了,可以弹出3,将3记录到后序遍历的数组中:

虽然8的右子树不为空,但是不能弹出8(理由见上),入8的右子树:

10的左和右子树为NULL,直接弹出10,将10记录到后序遍历的数组中:

第二次遇到8,因为8的左右子树都访问完了,可以弹出8,将8记录到后序遍历的数组中:

栈为空,循环结束

问题:如何确定是第一次访问到栈的元素还是第二次访问到栈中的元素?

上面提到了:"虽然3的右子树不为空,但是不能弹出3,如果弹出3那就成前序遍历了,应该等第二次访问到栈里面的3才弹出3(即将3的左右子树都访问完才能访问根节点3)"

方法1:使用填充的内存(依赖于架构)

得知题目条件"树中节点的数目在范围 [-100, 100] 内",而且TreeNode的val是用int存储的,如果val>0,那么最多只会占用int的低7位,如果val<0,那么int所有位都会占用

显然在val内部使用一个标志位来判断是第一次访问到栈的元素还是第二次访问到栈中的元素是不切实际的

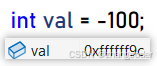
突破口:结构体的内存对齐

64位下,TreeNode结构体的内存分布图:

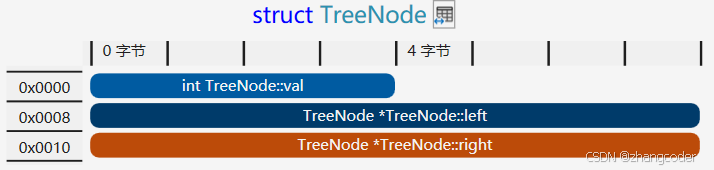
会发现0x0004~0x007是填充的4个字节,没有用处!

填充的字节可以借用其中一个字节来标记是第一次还是第二次访问到栈中的元素,简称为标志字节

例如选这一字节:

怎么从标志字节哪里得知是第一次还是第二次访问到栈中的元素呢?

对于填充的字节,编译器会给初始值,Linux下的值是0xBE,Windows下的值是0xCD,下面padding_byte获取到的就是初始字节(pad v.填充)

unsigned char padding_byte = *((unsigned char*)&(root->val) + 4);

那么第一次访问过节点后可以设置标志字节为指定值,让其不等于原来编译器给的初始值就行了,例如可以设置成0x01,等到第二次访问发现是0x01,就能让栈顶元素出栈,写入到后序遍历的数组中

如果LeetCode是64位架构且没有使用gcc的-m32选项,那么上述方法是可行的,可以用宏判断:

判断计算机使用的架构和指针大小
#if defined(__x86_64__) || defined(_M_X64)printf("This is a 64-bit x86 architecture\n");
#elif defined(__i386__)printf("This is a 32-bit x86 architecture\n");
#elif defined(__arm__) || defined(_M_ARM)printf("This is an ARM architecture\n");
#elif defined(__aarch64__) || defined(_M_AARCH64)printf("This is a 64-bit ARM architecture\n");
#elseprintf("Unknown architecture\n");
#endif//__SIZEOF_POINTER__是指针大小
if (__SIZEOF_POINTER__ == 4) 
{printf("This is a 32-bit architecture.\n");
} 
else if (__SIZEOF_POINTER__ == 8) 
{   printf("This is a 64-bit architecture.\n"); 
} 
else 
{printf("Unknown architecture.\n");
}

LeetCode输出结果:

使用填充的内存的方法是可行的

代码
class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;unsigned char padding_byte=*((unsigned char*)&(root->val)+4);stack<TreeNode*> st;TreeNode* cur = root;while (cur || !st.empty()){//先遍历左子树,但不访问其中的节点,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子树遍历完了,那就访问根和右子树auto elem = st.top();unsigned char* flag_byte_ptr=(unsigned char*)&(elem->val)+4;if (elem->right == nullptr){ret.push_back(elem->val);st.pop();continue;}if (*flag_byte_ptr!=padding_byte){//第二次访问到,说明左右子树都访问完了,必须重新设置curst.pop();ret.push_back(elem->val);continue;}else{//第一次访问到,要设置标志字节*flag_byte_ptr=1;}cur = elem->right;// 子问题的方式访问右子树}return ret;}
};
提交结果

方法2:寻找规律,设置一个prev变量记录上一个访问的节点

访问右子树有两种情况:右为空(不用管右直接拿出栈顶元素),右不为空(需要使用上一次访问的节点)

例如下图的节点的3会访问到两次:

由方法1的栈图分析

1.如果3的右子树没有访问过,上一次访问的是3的左子树的根1

↓ 

2..如果3的右子树访问过,上一次访问的是3的右子树的根6

↓ 

设置一个变量prev记录cur访问的前一个节点即可

代码
class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;TreeNode* prev = nullptr;while (cur || !st.empty()){//先遍历左子树,但不访问其中的节点,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子树遍历完了,那就访问根和右子树auto elem = st.top();if (elem->right == nullptr){prev=elem;ret.push_back(elem->val);st.pop();}if (prev==elem->right){//第二次访问到,说明左右子树都访问完了,必须重新设置curprev=elem;st.pop();ret.push_back(elem->val);}else//prev=cur->left{cur = elem->right;// 第一次访问到,子问题的方式访问右子树}   }return ret;}
};
运行结果

方法3:使用标记栈

标记栈的作用是标记对应的节点有没有访问过,是否访问过这个节点就看标记栈的栈顶值

代码
class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;stack<TreeNode*> st;stack<TreeNode*> flag;TreeNode* cur = root;while (cur || !st.empty()){//先遍历左子树,但不访问其中的节点,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子树遍历完了,那就访问根和右子树auto elem = st.top();if (elem->right == nullptr){ret.push_back(elem->val);st.pop();continue;}if (flag.size()&&flag.top()==elem){//第二次访问到,说明左右子树都访问完了,必须重新设置curst.pop();flag.pop();ret.push_back(elem->val);continue;}if (flag.empty() || flag.top()!=elem){//第一次访问到,要设置标志字节flag.push(elem);}cur = elem->right;// 子问题的方式访问右子树}return ret;}
};
运行结果

http://www.dtcms.com/a/356721.html

相关文章：

  • 4.渗透-.DOS命令（文件目录操作）
  • 响应式编程框架Reactor【3】
  • Rust Web框架Axum学习指南之响应和异常封装
  • 如何备份 TECNO 手机上的短信
  • 云手机的安全性如何？
  • 云手机技术中都有着哪些局限性？
  • 国际期货Level2分时Tick历史行情数据处理分析
  • 关于 etree 的解析
  • 【c++题解】经典题目：带修改的 LIS 问题——CF650D Zip-line
  • 【修复软件】【缺少dll、ocx】加载失败报错无法运行注册老软件崩溃解决修复任何软件等通用方法
  • 中文PDF解析工具测评与选型指南
  • MemoryVLA：让机器人拥有“记忆“的视觉-语言-动作模型
  • 第2.1节：AI大模型之GPT系列（GPT-3、GPT-4、GPT-5）
  • 深入解析Qt节点编辑器框架：高级特性与性能优化（四）
  • 性能测试-jmeter7-元件提取器
  • 达梦数据库-归档日志（一）
  • 达梦数据库-数据文件 (二)
  • 【ShiMetaPi M4-R1】上手：RK3568B2 |开源鸿蒙（OpenHarmony) 开发板上手指南
  • dm8_静默安装简单快速
  • 第一百零二章：AI的“未来电影制片厂CEO”：多模态系统落地项目实战（完整 AI 视频创作平台）
  • mongoDB学习（docker）
  • MYSQL速通（2/5）
  • 【开题答辩全过程】以 基于Spring Boot的网上家庭烹饪学习系统的设计与实现为例，包含答辩的问题和答案
  • 软考-系统架构设计师 办公自动化系统(OAS)详细讲解
  • LeetCode 完全背包 279. 完全平方数
  • 小程序版碰一碰发视频：源码搭建与定制化开发的源头技术解析
  • Java开发MongoDB常见面试题及答案
  • [TG开发]与Reids集成
  • five86: 2靶场渗透
  • LangChain实战（二）：环境搭建与Hello World（国内开源模型版）