Python计算点云的均值、方差、标准差、凸点(顶点)、质心和去中心化
今天我们分享点云几个特征的计算方法,介绍如下:
1. 点云的均值
1.1 原理
点云的均值是指点云中所有点的平均位置,它表示点云的中心位置。均值的计算公式为:
mu = frac{1}{N} sum_{i=1}^{N} x_i ]
其中,( x_i ) 是第 ( i ) 个点的坐标,( N ) 是点的总数。1.2 实现步骤
1)读取点云数据:从文件中读取点云数据。
2)提取点云坐标:将点云对象中的点数据提取为 numpy 数组。
3)计算均值:使用 numpy 的 mean 函数计算点云坐标的均值。2. 点云的方差
2.1原理
方差描述点云中点到均值的平均距离的平方,表示点云的离散程度。方差的计算公式为:
sigma^2 = frac{1}{N} sum_{i=1}^{N} (x_i - mu)^2 ]2.2 实现步骤
1)读取点云数据:从文件中读取点云数据。
2)提取点云坐标:将点云对象中的点数据提取为 numpy 数组。
3)计算均值:使用 numpy 的 mean 函数计算点云坐标的均值。
4)计算方差:使用 numpy 的 var 函数计算点云坐标的方差。3. 点云的标准差
3.1 原理
标准差是方差的平方根,也表示点云的离散程度,但与原始数据的尺度一致。标准差的计算公式为:
sigma = sqrt{sigma^2}3.2 实现步骤
1)读取点云数据:从文件中读取点云数据。
2)提取点云坐标:将点云对象中的点数据提取为 numpy 数组。
3)计算均值:使用 numpy 的 mean 函数计算点云坐标的均值。
4)计算方差:使用 numpy 的 var 函数计算点云坐标的方差。
5)计算标准差:使用 numpy 的 std 函数计算点云坐标的标准差。4. 点云的凸包
4.1 原理
凸包是指在实向量空间 \( \mathbb{R}^n \) 中的一组点 ( X ) 的凸包或凸包络是包含 ( X ) 的最小凸集。通俗地说就是包围一组散点的最小凸多边形。三维点云的凸包是包含所有点的最小凸集,Open3D 中的 `compute_convex_hull` 函数实现了计算凸包的方法。4.2 实现步骤
1)读取点云数据:从文件中读取点云数据。
2)计算凸包:使用 Open3D 的 `compute_convex_hull` 函数计算点云的凸包。
3)可视化凸包:使用 Open3D 可视化计算得到的凸包。5. 点云的质心
5.1 原理
在 Open3D 中,计算点云 \( Q \) 的质心(中心点)是一个常见的操作。质心是点云所有点的平均位置,可以通过简单地计算点云中所有点的平均值来得到。点云质心的计算是点云处理中一个基本且重要的步骤。质心不仅是点云的几何中心,还在许多实际应用中起着重要作用,包括点云对齐、归一化、重心调整、特征提取、可视化和机器人导航等。通过计算质心,可以更有效地处理和分析点云数据,提升点云处理任务的精度和效率。5.2 实现步骤
1)提取点云数据:将点云数据表示为一组三维坐标点( (x_i, y_i, z_i)),其中( i = 1, 2, ..., N) 表示点的索引,(N) 为点云中的点数。
2)计算各个坐标轴上的平均值:
-( x ) 坐标的平均值(bar{x} = frac{1}{N} sum_{i=1}^{N} x_i )
- ( y ) 坐标的平均值(bar{y} = frac{1}{N} sum_{i=1}^{N} y_i )
- ( z ) 坐标的平均值(bar{z} = frac{1}{N} sum_{i=1}^{N} z_i )
3)质心坐标:质心坐标为 ( (bar{x}, bar{y}, bar{z}) ),即点云中所有点坐标的平均值。6. 点云的去中心化
6.1 原理
在 Open3D 中,计算去质心后的点云 \( Q \) 是一个常见的操作,尤其是在点云配准、对齐和归一化过程中。去质心操作是将点云的质心平移到原点,使得点云数据相对于原点对称分布。6.2 实现步骤
1)读取点云数据:读取点云文件。
2)计算质心:计算点云中所有点的质心。
3)平移点云:将点云中所有点平移,使质心位于原点。
4)可视化去质心后的点云:使用 Open3D 可视化去质心后的点云。
本次我们的数据,你猜猜————————————猜对啦!兔砸,哈哈哈
一、各种特征计算程序
import open3d as o3d
import numpy as np
import os
import tkinter as tk
from tkinter import messagebox# ===== 唯一需要修改的地方:你的点云完整路径 =====
PCD_PATH = r'E:/CSDN/规则点云/bunny.pcd'
# =====================================================if not os.path.isfile(PCD_PATH):messagebox.showerror("错误", f"找不到点云:\n{PCD_PATH}")exit()pcd = o3d.io.read_point_cloud(PCD_PATH)
if not pcd.has_points():messagebox.showerror("错误", "点云为空或读取失败")exit()pts = np.asarray(pcd.points)# -------------------- 功能封装 --------------------
def show_stats():mean = np.mean(pts, axis=0)var = np.var(pts, axis=0)std = np.std(pts, axis=0)messagebox.showinfo("统计量",f"均值:{mean}\n"f"方差:{var}\n"f"标准差:{std}")def show_convex():hull, _ = pcd.compute_convex_hull()lines = o3d.geometry.LineSet.create_from_triangle_mesh(hull)lines.paint_uniform_color((1, 0, 0))o3d.visualization.draw_geometries([pcd, lines], window_name="Convex Hull")def show_centroid():c = np.mean(pts, axis=0)frame = o3d.geometry.TriangleMesh.create_coordinate_frame(size=0.1)frame.translate(c)o3d.visualization.draw_geometries([pcd, frame], window_name="Centroid")def center_and_save():c = np.mean(pts, axis=0)centered = o3d.geometry.PointCloud()centered.points = o3d.utility.Vector3dVector(pts - c)if pcd.has_colors():centered.colors = pcd.colorsif pcd.has_normals():centered.normals = pcd.normals# 需要保存的话把下面注释取消掉# out = os.path.join(os.path.dirname(PCD_PATH), "centered_1.pcd")# o3d.io.write_point_cloud(out, centered, write_ascii=True)# messagebox.showinfo("完成", f"已保存:\n{out}")# 可视化对比pcd.paint_uniform_color((0, 1, 0))centered.paint_uniform_color((1, 0, 0))centered.translate([0, 0.002, 0])o3d.visualization.draw_geometries([pcd, centered],window_name="Original vs Centered")# -------------------- 简单 GUI --------------------
def on_click(mode):if mode == 1:show_stats()elif mode == 2:show_stats() # 一并打印elif mode == 3:show_stats()elif mode == 4:show_convex()elif mode == 5:show_centroid()elif mode == 6:center_and_save()root = tk.Tk()
root.title("计算小工具")
root.geometry("260x220")tk.Label(root, text="请选择要执行的操作:", font=("微软雅黑", 12)).pack(pady=5)for i, txt in enumerate(["1 均值", "2 方差", "3 标准差","4 凸包顶点", "5 质心", "6 去中心化"],start=1):tk.Button(root, text=txt, width=20,command=lambda m=i: on_click(m)).pack(pady=2)tk.Button(root, text="退出", width=20, command=root.quit).pack(pady=8)root.mainloop()二、各种特征计算结果
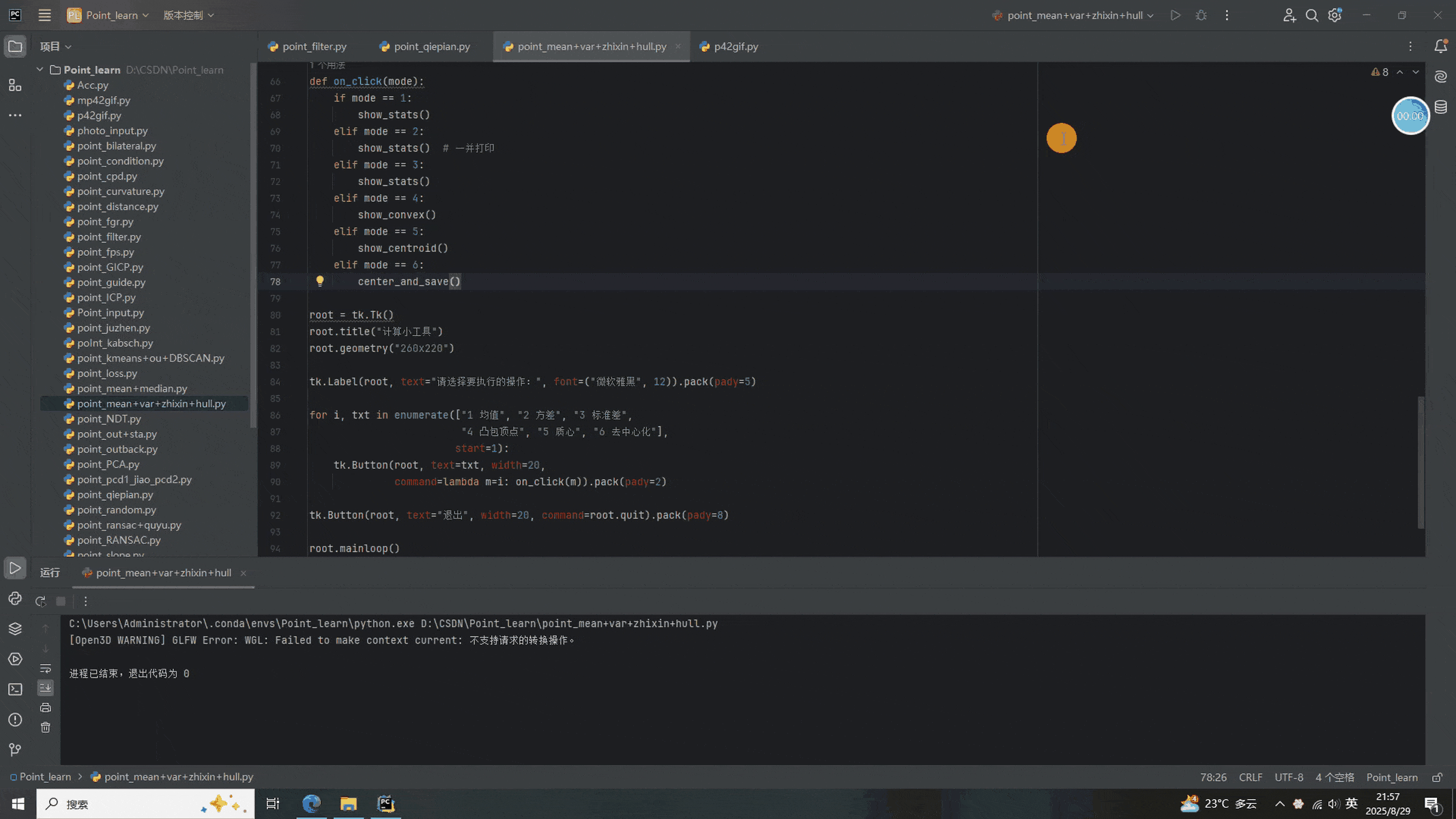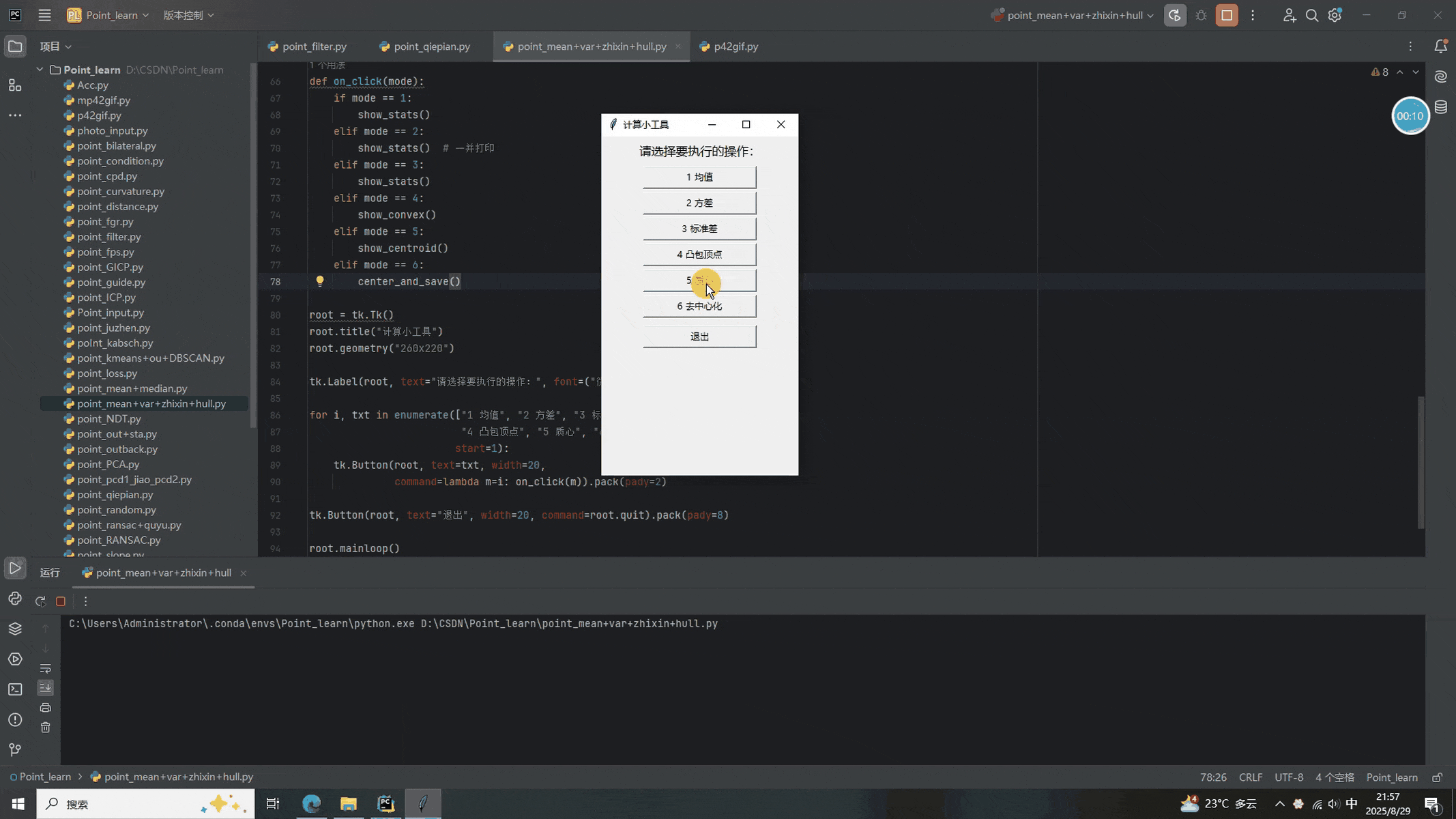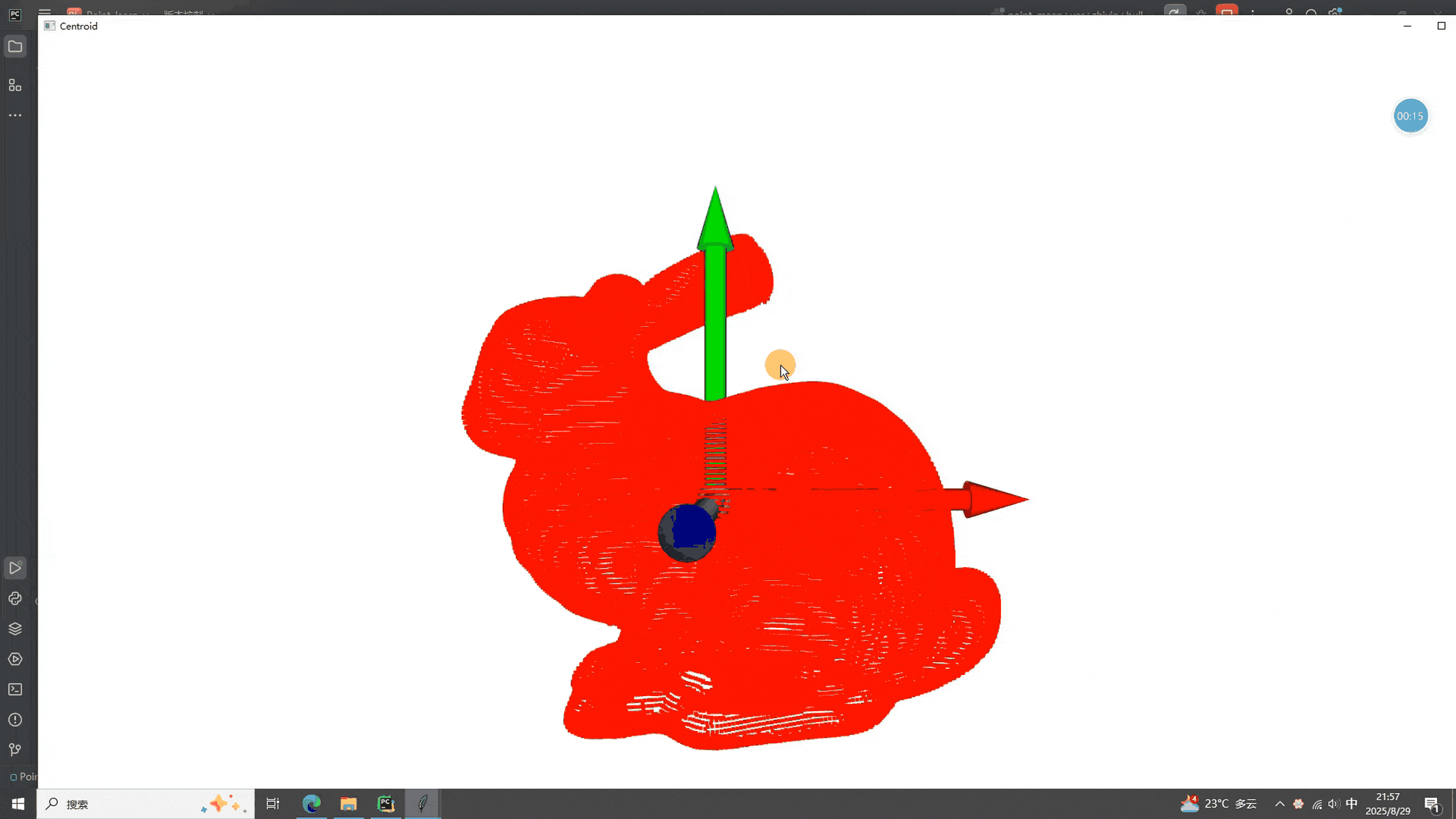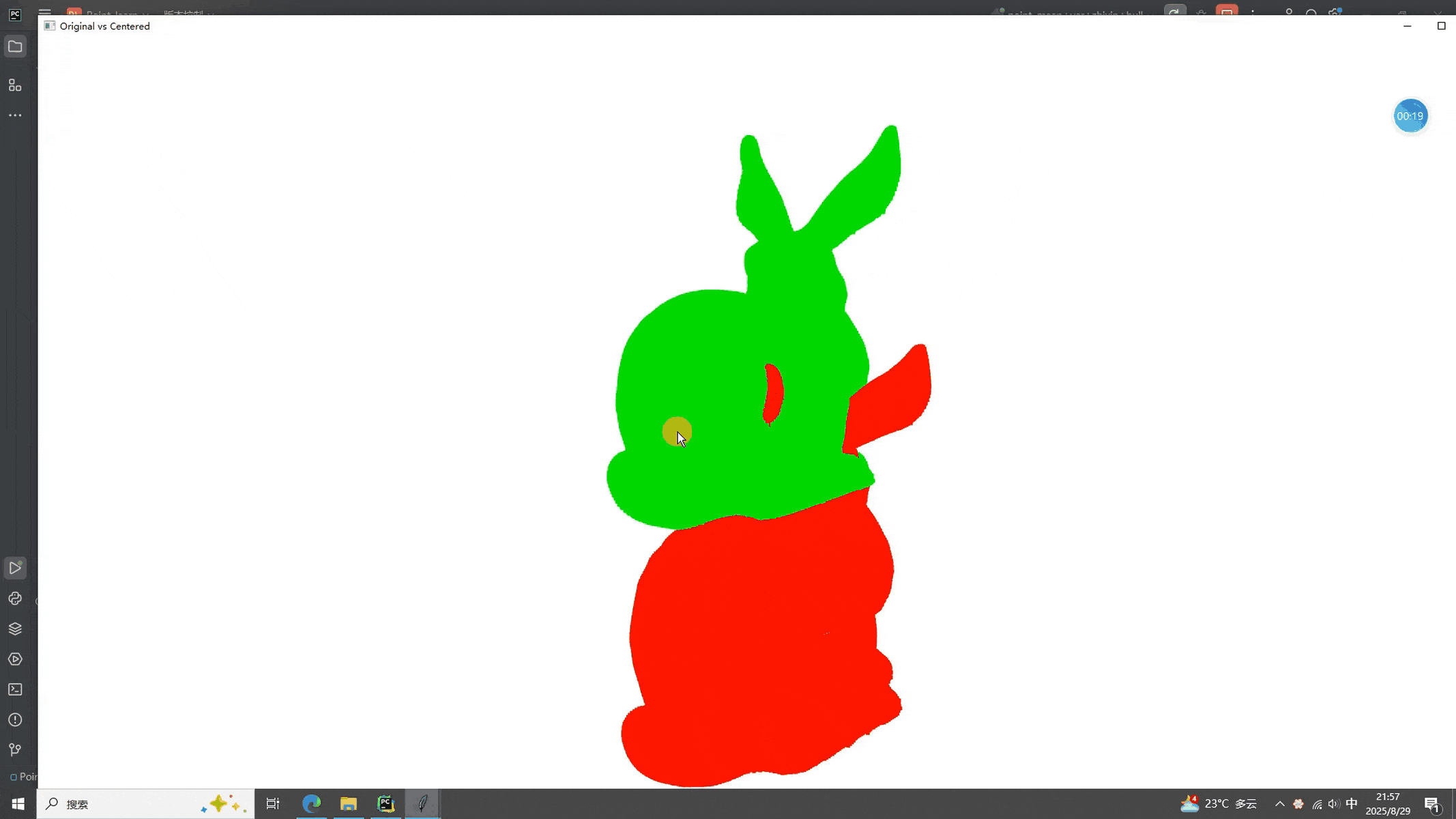
本次我们为了方便操作,做了一个gui界面。可以看到,均值、方差和标准差被一块显示出来了,三个按钮的显示结果一样,凸包、质心和去中心化也很好的计算了(同学甲:那么快我看个吉尔!作者:没办法啊,平台限制大小,自己运行下看看呗。。)
就酱,下次见^-^
