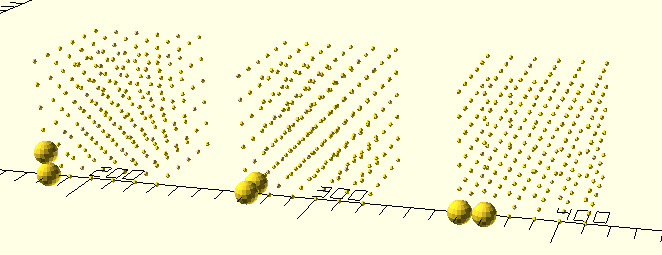
整理3点结构点与点之间的距离

在3维yz，xz，xy面可自由变换的条件下，2点结构有7个

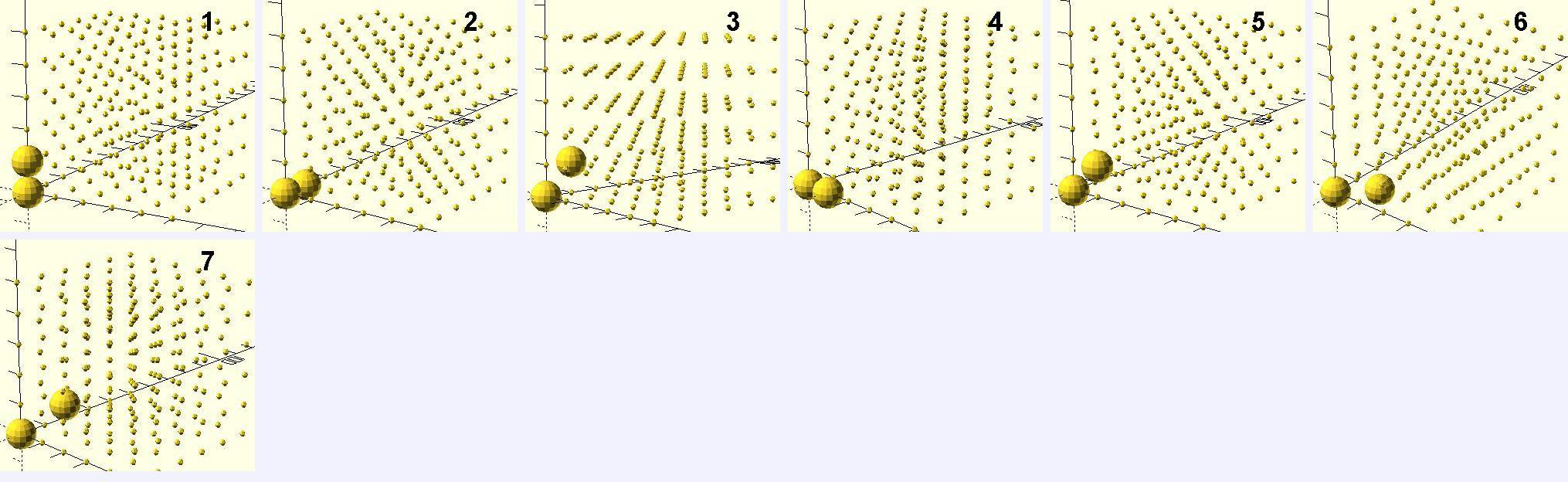
在2*2*2的空间中随机取2个点统计两个点之间的距离和分类得到

2*2*2	数量	距离	平均值
1	4	4	1
2	4	4	1
3	4	5.6569	1.4142
4	4	4	1
5	4	5.6569	1.4142
6	4	5.6569	1.4142
7	4	6.9282	1.7321
	28

在3*3*3和4*4*4的条件下再次统计得到

3*3*3	数量	距离	平均值		4*4*4	数量	距离	平均值
1	27	36	1.3333			96	160	1.6667
2	27	36	1.3333			96	160	1.6667
3	54	104.58	1.9366			288	708.1	2.4587
4	27	36	1.3333			96	160	1.6667
5	54	104.58	1.9366			288	708.1	2.4587
6	54	104.58	1.9366			288	708.1	2.4587
7	108	258.86	2.3968			864	2644.2	3.0604
	351					2016

无论空间的尺寸多大，两个点之间的距离都只有3个梯度。

在3维yz，xz，xy面可自由变换的条件下，3点结构有29个

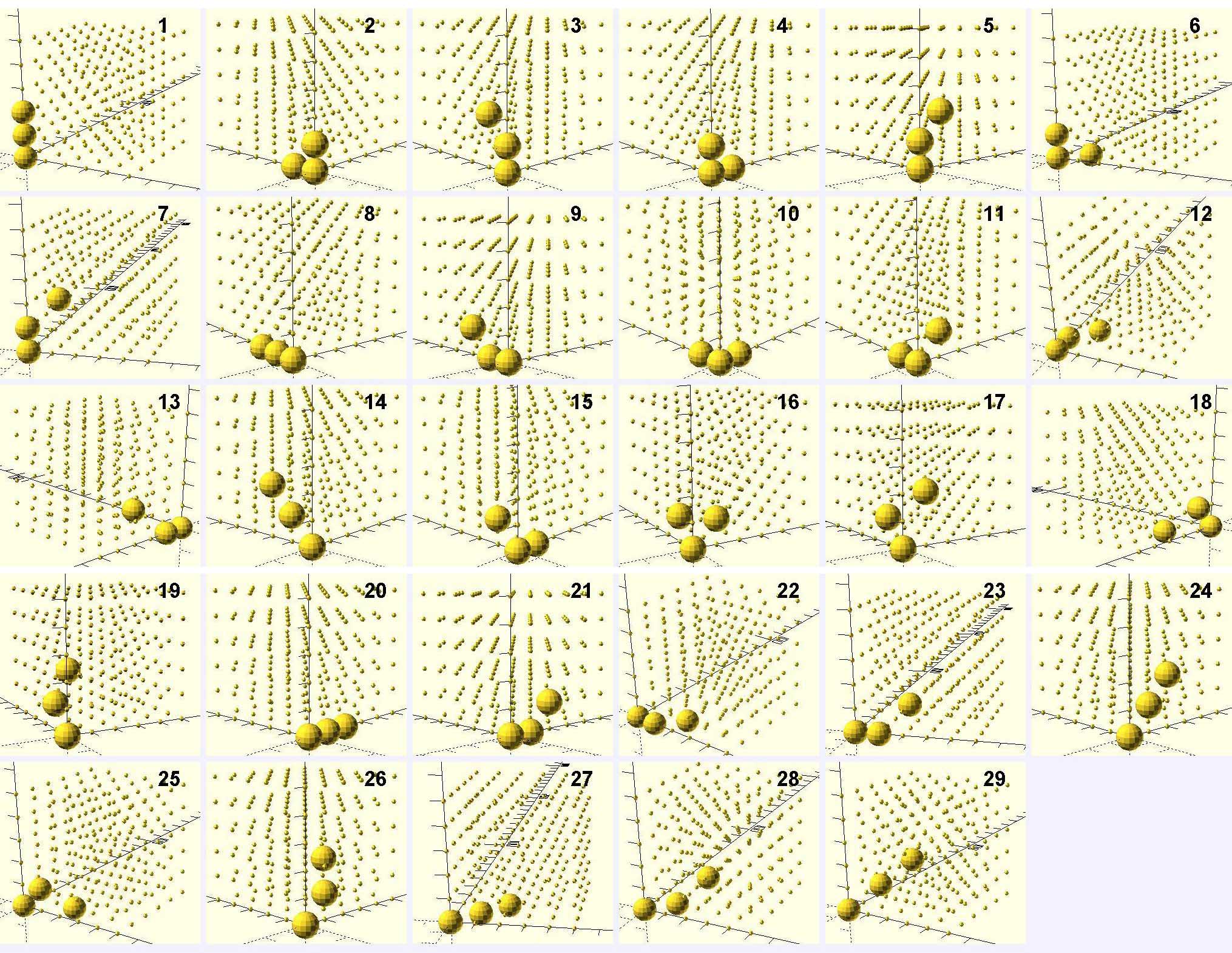
用同样的办法统计得到

3*3*3	数量	距离	平均			4*4*4	数量	距离	平均
1	9	36	4	1		1	64	320	5
8	9	36	4	1		8	64	320	5
20	9	36	4	1		20	64	320	5
2	108	497.15	4.603	2		2	576	3336.2	5.792
10	108	497.15	4.603	2		4	576	3336.2	5.792
4	108	497.15	4.603	2		10	576	3336.2	5.792
3	54	281.15	5.207	3		9	576	3792.4	6.584
5	54	281.15	5.207	3		12	576	3792.4	6.584
9	54	281.15	5.207	3		5	576	3792.4	6.584
12	54	281.15	5.207	3		22	576	3792.4	6.584
21	54	281.15	5.207	3		21	576	3792.4	6.584
22	54	281.15	5.207	3		3	576	3792.4	6.584
6	216	1224	5.667	4		11	1728	12417	7.186
11	216	1224	5.667	4		15	1728	12417	7.186
15	216	1224	5.667	4		6	1728	12417	7.186
16	216	1254.9	5.81	5		16	1728	12746	7.376
14	18	104.58	5.81	5		24	384	2832.4	7.376
24	18	104.58	5.81	5		27	384	2832.4	7.376
27	18	104.58	5.81	5		14	384	2832.4	7.376
7	108	661.72	6.127	6		23	1728	13457	7.787
13	108	661.72	6.127	6		7	1728	13457	7.787
23	108	661.72	6.127	6		13	1728	13457	7.787
17	216	1354.3	6.27	7		17	3456	27571	7.978
18	216	1354.3	6.27	7		25	3456	27571	7.978
25	216	1354.3	6.27	7		18	3456	27571	7.978
19	108	726.87	6.73	8		28	3456	29651	8.579
26	108	726.87	6.73	8		26	3456	29651	8.579
28	108	726.87	6.73	8		19	3456	29651	8.579
29	36	258.86	7.19	9		29	2304	21153	9.181
	2925						41664

在3*3*3的条件下3点结构有2925个，在4*4*4的条件下3点结构有41664个。但无论是在3*3*3或在4*4*4的条件下3点结构都只有9个梯度

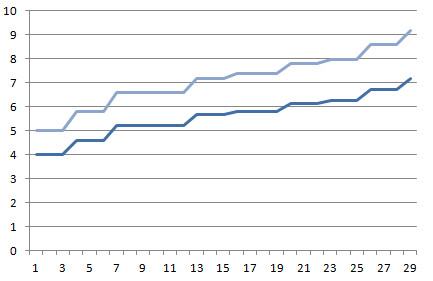
特别是16，14，24，27这一组，他们的平均距离是一样的

所以能级一样结构未必相同。

由结构加法

9(2t1+1)=3*3t1+3t2+3t3+3t4+3t5+3t6+3t7

9(2t2+1)=3t2+3*3t8+3t9+3t10+3t11+3t12+3t13

13(2t3+1)=3t2+2*3t3+2*3t9+3*3t14+3t15+3t16+3t17+3t18+3t19

9(2t4+1)=3t4+3t10+3t15+3*3t20+3t21+3t22+3t23

13(2t5+1)=3t4+2*3t5+3t11+3t16+3t17+2*3t21+3*3t24+3t25+3t26

13(2t6+1)=3t6+3t10+2*3t12+3t16+3t18+2*3t22+3t25+3*3t27+3t28

21(2t7+1)=3t6+2*3t7+3t11+2*3t13+3t15+3t17+3t18+2*3t19+2*3t23+3t25+2*3t26+2*3t28+3*3t29

把3点的9个梯度代入等式

如代入1，2，3，2，…，9得到

计算梯度
2.555556	1
2.555556	2
4.615385	3
2.555556	4
4.615385	5
4.615385	6
6.857143	7

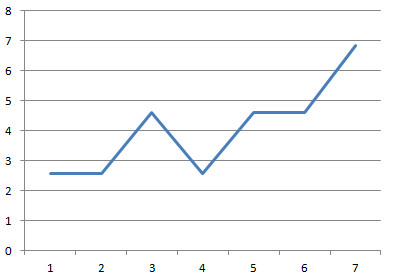
所以梯度也符合结构加法，用梯度重写2点结构的等式得到

9*（s2(1)+1）=3*s3(1)+s3(2)+s3(3)+s3(2)+s3(3)+s3(4)+s3(6)

9*（s2(1)+1）=s3(2)+3*s3(1)+s3(3)+s3(2)+s3(4)+s3(3)+s3(6)

13*（s2(2)+1）=s3(2)+2*s3(3)+2*s3(3)+3*s3(5)+s3(4)+s3(5)+s3(7)+s3(7)+s3(8)

9*（s2(1)+1）=s3(2)+s3(2)+s3(4)+3*s3(1)+s3(3)+s3(3)+s3(6)

13*（s2(2)+1）=s3(2)+2*s3(3)+s3(4)+s3(5)+s3(7)+2*s3(3)+3*s3(5)+s3(7)+s3(8)

13*（s2(2)+1）=s3(4)+s3(2)+2*s3(3)+s3(5)+s3(7)+2*s3(3)+s3(7)+3*s3(5)+s3(8)

21*（s2(3)+1）=s3(4)+2*s3(6)+s3(4)+2*s3(6)+s3(4)+s3(7)+s3(7)+2*s3(8)+2*s3(6)+s3(7)

+2*s3(8)+2*s3(8)+3*s3(9)

这里s2（1）表示2点结构位于第一个梯度，所以函数

9*（s2(1)+1）=3*s3(1)+s3(2)+s3(3)+s3(2)+s3(3)+s3(4)+s3(6)

对应的运动就是